Spațiu vectorial

Adunarea între vectori și înmulțirea cu un scalar: un vector v (albastru) este compus cu un alt vector w (roșu, imaginea de sus). Mai jos, w este întins cu un factor de 2, obținându-se suma v + 2w.

Un spațiu vectorial (numit și spațiu liniar) este o colecție de obiecte numite vectori, care pot fi adunați între ei și înmulțiți („scalați”) cu numere, denumite în acest context scalari. Scalarii sunt de multe ori luați ca numere reale, dar există și spații vectoriale în care înmulțirea cu un scalar se face cu numere complexe, numere raționale, sau, în general, din orice corp comutativ. Operațiunile de adunare vectorială și de înmulțire cu un scalar trebuie să îndeplinească anumite cerințe, numite axiome, enumerate mai jos.

Vectorii euclidieni sunt un exemplu de spațiu vectorial. Ei reprezintă cantități fizice, cum ar fi forțele: orice două forțe (de același tip) pot fi adunate pentru a produce o a treia, și înmulțirea unui vector forță cu un factor de înmulțire real dă un alt vector forță. În același fel, dar într-un sens mai geometric, vectorii care reprezintă deplasări în plan sau în spațiul tridimensional formează și ei spații vectoriale. Vectorii din spațiile vectoriale nu trebuie să fie neapărat obiecte reprezentabile prin săgeți, așa cum apar în exemplele amintite: vectorii sunt considerați ca abstracții matematice, obiecte cu proprietăți speciale, care în unele cazuri pot fi reprezentate sub forma unor săgeți.

Spațiile vectoriale fac obiectul algebrei liniare și sunt bine caracterizate prin dimensiunea lor, care, aproximativ vorbind, specifică numărul de direcții independente în spațiu. Spații vectoriale infinit-dimensionale apar în mod natural în analiza matematică, ca spații de funcții, ale căror vectori sunt funcții. Aceste spații vectoriale sunt, în general, înzestrate cu o structură suplimentară, care poate fi o topologie, care să permită luarea în considerare a aspectelor de proximitate și de continuitate. Printre aceste topologii, cele definite printr-o normă sau produs scalar sunt mai frecvent utilizate, ca având o noțiune de distanță dintre doi vectori. Este în special cazul spațiilor Banach și spațiilor Hilbert, care sunt fundamentale în analiza matematică.

Din punct de vedere istoric, primele idei care au condus la noțiunea de spațiu vectorial pot fi găsite în geometria analitică, matricile, sistemele de ecuații liniare, și vectorii euclidieni din secolul al XVII-lea. Abordarea modernă, mai abstractă, formulată pentru prima dată de către Giuseppe Peano în 1888, cuprinde obiecte mai generale decât spațiul euclidian, dar o mare parte din teorie poate fi văzută ca o extensie ideilor din geometria clasică, cum ar fi drepte, planuri și analogii în dimensiuni superioare.

Astăzi, spațiile vectoriale au aplicații în toată matematica, în științe și inginerie. Acestea sunt noțiunile liniar-algebrice adecvate pentru a trata sisteme de ecuații liniare; a oferi un cadru pentru dezvoltarea în serie Fourier, utilizată în rutinele de compresie a imaginilor; sau a oferi un mediu care poate fi folosit pentru tehnici de rezolvare a ecuațiilor cu derivate parțiale. Mai mult, spațiile vectoriale furnizează o modalitate abstractă, independentă de coordonate, de a trata obiecte fizice sau geometrice, cum ar fi tensorii. Aceasta, la rândul său, permite examinarea proprietăților locale ale varietăților prin tehnici de liniarizare. Spațiile vectoriale pot fi generalizate în mai multe moduri, ceea ce duce la mai multe noțiuni avansate în geometrie și algebra abstractă.

Introducere și definiții

Conceptul de spațiu vectorial va fi explicat în primul rând prin descrierea a două exemple concrete:

Primul exemplu: săgeți în plan

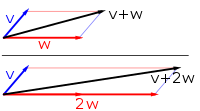
Primul exemplu de spațiu vectorial constă din săgeți într-un plan, pornind de la un punct fix (originea). Acestea sunt folosite în fizică pentru a descrie forțele sau vitezele. Date fiind oricare două astfel de săgeți, v și w, paralelogramul generat de aceste două săgeți conține o săgeată diagonală care începe și ea tot de la origine. Această nouă săgeată se numește suma celor două săgeți și este notată cu v + w. În cazul special când cele două săgeți sunt pe aceeași linie, suma lor este săgeata de pe această linie a cărui lungime este suma sau diferența de lungimi, în funcție dacă săgețile au același sens sau sensuri opuse. O altă operație care se poate face cu săgeți este scalarea: dat fiind orice număr real pozitiv a, săgeata care are aceeași direcție ca și v, dar este dilatată sau micșorată prin înmulțirea lungimii sale cu a, se numește înmulțire a lui v cu a. Acesta este notată av. Atunci când a este negativ, av este definit ca fiind o săgeată îndreptată în sens opus, pe aceeași direcție.

Următoarele arată câteva exemple: dacă a = 2, vectorul rezultat aw are aceeași direcție ca și w, dar este întins la lungime dublă față de w (dreapta imaginii de mai jos). Echivalent, 2w este suma w + w. În plus, (-1)v = −v are sens opus și aceeași lungime ca v (vectorul albastru cu vârful în jos în imaginea din dreapta).

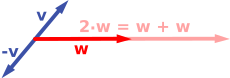
Al doilea exemplu: perechi ordonate de numere

Un al doilea exemplu de spațiu vectorial este dat ca perechile de numere reale x și y. (Ordinea componentelor x și y este importantă, astfel încât o astfel de pereche se numește și pereche ordonată.) O astfel de pereche este scrisă sub forma (x, y). Suma a două astfel de perechi și înmulțirea unei perechi cu un număr sunt definite după cum urmează:

(x₁, y₁) + (x₂, y₂) = (x₁ + x₂, y₁ + y₂)

și

a (x, y) = (ax, ay).

Primul exemplu de mai sus se reduce la acesta dacă săgețile sunt reprezentate printr-o pereche de coordonate carteziene ale punctelor lor de capăt.

Definiție

Un spațiu vectorial peste un corp comutativ K este structura formată dintr-o mulțime V împreună cu două operații, care satisface cele opt axiome enumerate mai jos. Elementele din V sunt de obicei numite vectori. Elementele din K sunt de obicei numite scalari. Prima operațiune, numită adunare vectorială sau pur și simplu adunare, ia orice doi vectori v și w și le atribuie un al treilea vector, care este de obicei scris ca v + w, și se numește suma acestor doi vectori. Cea de-a doua operație, numită înmulțire cu un scalar, ia orice scalar și orice vector v și dă un alt vector.

În acest articol, vectorii sunt deosebiți de scalari prin aceea că sunt scriși cu litere îngroșate. În cele două exemple de mai sus, corpul este corpul numerelor reale și mulțimea vectorilor este formată din săgeți plane având un punct fix de pornire și, respectiv, din perechi de numere reale.

Pentru a se califica drept spațiu vectorial, mulțimea V și operațiile de adunare și înmulțire cu un scalar trebuie să respecte o serie de cerințe numite axiome. În lista de mai jos, fie u, v și w vectori arbitrari din V, și a și b scalari din K.

Axioma	Înțelesul
Asociativitatea adunării	u + (v + w) = (u + v) + w
Comutativitatea adunării	u + v = v + u
Elementul neutru al adunării	Există un element 0 ∈ V, numit vectorul nul, astfel încât v + 0 = v pentru orice v ∈ V.
Elementul simetric al adunării	Pentru fiecare v ∈ V, există un element −v ∈ V, numit opusul lui v, astfel încât v + (−v) = 0.
Compatibilitatea⁠(d) înmulțirii cu un scalar cu înmulțirea corpului	a(bv) = (ab)v
Elementul neutru al înmulțirii cu un scalar	1v = v, unde 1 reprezintă elementul neutru multiplicativ din K.
Distributivitatea înmulțirii cu un scalar față de adunarea vectorială	a(u + v) = au + av
Distributivitatea înmulțirii cu un scalar în raport cu operatorul aditiv al corpului	(a + b)v = av + av

Aceste axiome generalizează proprietățile vectorilor introduse în exemplele de mai sus. Într-adevăr, rezultatul adunării a două perechi ordonate (ca în al doilea exemplu de mai sus) nu depinde de ordinea operanzilor:

(x_v, y_v) + (x,_w, y,_w) = (x,_w, y,_w) + (x_v, y_v).

De asemenea, în exemplul geometric în care vectorii erau văzuți ca săgeți, v + w = w + v întrucât paralelogramul care definește adunarea vectorilor este independent de ordinea vectorilor. Toate celelalte axiome pot fi verificate într-un mod similar în ambele exemple. Astfel, făcând abstracție de natura concretă a tipului particular de vectori pe care se lucrează, definiția include aceste două exemple, și multe altele, într-o singură noțiune unificatoare de spațiu vectorial.

Scăderea a doi vectori și împărțirea la un scalar nenul poate fi definită ca:

v − w = v + (−w),

v/a = (1/a)v.

Atunci când corpul de scalari K este mulțimea numerelor reale R, spațiul vectorial se numește spațiu vectorial real. Atunci când câmpul scalar este mulțimea numerelor complexe, se numește spațiu vectorial complex. Aceste două cazuri sunt cele folosite cel mai adesea în inginerie. Definiția generală a unui spațiu vectorial permite ca scalarii să fie elemente din orice corp comutativ fix K, spațiul fiind denumit în acest caz spațiu vectorial peste K. Un corp comutativ este, în esență, o mulțime de numere care posedă operațiuni de adunare, scădere, înmulțire și împărțire. De exemplu, numerele raționale formează și ele un corp comutativ.

Spre deosebire de analogia intuitivă care decurge din asocierea lor cu vectori în plan și din cazurile de dimensiune superioară, în spațiile vectoriale generale, nu există nicio noțiune de vecinătate, unghi sau distanță. Pentru tratarea unor astfel de probleme, se introduc tipuri particulare de spații vectoriale; vedeți mai jos.

Formule alternative și consecințe elementare

Adunarea vectorială și înmulțirea cu un scalar sunt operațiuni care îndeplinesc proprietatea de închidere: u + v și av în V pentru a din K, u, v din V. Unele surse mai vechi menționează aceste proprietăți ca axiome separate.

În limbajul algebrei abstracte, primele patru axiome pot fi subsumate prin impunerea condiției ca mulțimea de vectori să fie un grup abelian în raport cu adunarea. Restul de axiome conferă acestui grup o structură de K-modul^⁠(d). Cu alte cuvinte, există un omomorfism de inele^⁠(d) f definit pe corpul K cu valori în inelul de endomorfisme^⁠(d) al grupului vectorilor. Atunci, înmulțirea cu un scalar av este definită ca (f(a))(v).

Există o serie de consecințe directe ale axiomelor spațiilor vectoriale. Unele dintre ele rezultă din aplicarea teoriei elementare a grupurilor asupra grupului aditiv al vectorilor: de exemplu, vectorul zero 0 din V și elementul invers −v al oricărui vector v sunt unice. Alte proprietăți rezultă din legea distributivității, de exemplu av este egal cu 0 dacă și numai dacă a este egal cu 0 sau v este egal cu 0.

Istorie

Spațiile vectoriale rezultă din geometria afină prin introducerea de coordonate în plan sau în spațiul tridimensional. În preajma lui 1636, Descartes și Fermat au pus bazele geometriei analitice prin echivalarea soluțiilor unei ecuații cu două variabile, cu puncte de pe o curbă plană. În 1804, pentru a obține soluții geometrice fără utilizarea de coordonate, Bolzano a introdus anumite operațiuni pe puncte, linii și planuri, predecesoarele vectorilor. Lucrarea sa a fost apoi utilizată în conceperea coordonatelor baricentrice^⁠(d) de către Möbius în 1827. În 1828, C. V. Mourey^⁠(d) sugera existența unei algebre care depășește nu numai algebra obișnuită, ci și algebra bidimensională creată de el în timp ce căuta o interpretare geometrică a numerelor complexe.

Definiția vectorilor s-a bazat pe noțiunea lui Bellavitis de bipunct, un segment orientat din care un capăt este originea și altul o țintă, și apoi elaborată în continuare cu prezentarea numerelor complexe de către Argand și Hamilton și introducerea cuaternionilor și bicuaternionilor^⁠(d) de către acesta din urmă. Acestea sunt elemente din R², R⁴ și R⁸; tratarea lor drept combinații liniare^⁠(d) poate fi găsită la Laguerre în 1867, care și el a definit sisteme de ecuații liniare.

În 1857, Cayley a introdus notația matriceală, care permite o armonizare și o simplificare a aplicațiilor liniare. În același timp, Grassmann a studiat calculul baricentric inițiat de Möbius. El și-a imaginat mulțimi de obiecte abstracte dotate cu operațiuni. În lucrarea sa sunt prezente conceptele de liniar-independență^⁠(d) și dimensiune, precum și cea de produs scalar. În fapt, activitatea lui Grassmann din 1844 depășește cadrul spațiilor vectoriale, deoarece abordarea înmulțirii l-a condus pe el la ceea ce astăzi numim algebre. Peano a fost primul care a dat definiția modernă a spațiilor vectoriale și a aplicațiilor liniare în 1888.

O dezvoltare importantă în domeniul spațiilor vectoriale se datorează construcției spațiilor de funcții de către Lebesgue. Ulterior, aceasta a fost formalizată de către Banach și Hilbert, în preajma anului 1920. La acea vreme, algebra și noul domeniu al analizei funcționale au început să interacționeze, în special cu concepte-cheie, cum ar fi spațiile de funcții p-integrabile și spațiile Hilbert. Spațiile vectoriale, inclusiv cele infinit-dimensionale, au devenit mai târziu noțiuni ferm stabilite, și multe ramuri matematice au început să facă uz de aceste concepte.

Exemple

Spații de coordonate

Cel mai simplu exemplu de spațiu vectorial peste un corp comutativ K este corpul însuși, echipat cu adunarea și înmulțirea standard. Mai mult, în general, un spațiu vectorial poate fi compus din n-tupluri^⁠(d) (secvențe de lungime n) de elemente din K, cum ar fi

(a₁, a₂, ..., a_n), unde fiecare a_i este un element din K.

Un spațiu vectorial compus din toate n-tuplurile unui corp K este cunoscut drept spațiu de coordonate^⁠(d), de obicei, notat cu Kⁿ. Cazul n = 1 este mai sus-menționatul exemplu simplu, în care corpul K este considerat și spațiu vectorial peste el însuși. Cazurile K = R și n = 2 au fost discutate în introducerea de mai sus.

Numerele complexe și alte extinderi ale corpului

Mulțimea numerelor complexe C, de exemplu, numere care pot fi scrise sub forma x + iy pentru x și y numere reale, unde i este unitatea imaginară, formează un spațiu vectorial peste numerele reale cu obișnuitele operațiuni de adunare și înmulțire cu un scalar: (x + iy) + (o + ib) = (x + o) + i(y + b) și c ⋅ (x + iy) = (c ⋅ x) + m(c ⋅ y) pentru numerele reale x, y, a, b și c. Diferite axiome ale spațiilor vectoriale rezultă din faptul că aceleași reguli rămân valabile pentru aritmetica numerelor complexe.

De fapt, exemplul numerelor complexe este, în esență, aceleași (adică este izomorf) cu spațiul vectorial al perechilor ordonate de numere reale menționat mai sus: dacă ne gândim la numărul complex x + i y ca reprezentând perechea ordonată (x, y) în planul complex, atunci vom vedea că regulile pentru sumă și produs scalar corespund exact cu cele din exemplul anterior.

Mai mult, în general, extinderile de corp oferă o altă clasă de exemple de spații vectoriale, în special în algebră și teoria algebrică a numerelor^⁠(d): un corp K care conține un corp mai mic E este spațiu vectorial peste E, prin operațiunile de înmulțire și de adunare date din K. De exemplu, numerele complexe sunt un spațiu vectorial peste R, iar extinderea de corp $\mathbf {Q} (i{\sqrt {5}})$ este un spațiu vectorial peste Q.

Spații de funcții

Funcțiile definite pe orice mulțime fixă Ω cu valori într-un corp comutativ K formează și ele spații vectoriale, prin efectuarea punctuală a operațiunilor de adunare și înmulțire cu un scalar. Adică suma a două funcții f și g este funcția (f + g) dată de

(f + g)(w) = f(w) + g(w),

și în mod similar pentru înmulțire. Astfel de spații funcționale apar în multe situații geometrice, atunci când Ω este dreapta reală sau un interval, sau alte submulțimi ale lui R. Multe noțiuni de topologie și analiză, cum ar fi continuitatea, integrabilitatea sau derivabilitatea se comportă bine în raport cu liniaritatea: adunarea și înmulțirea cu un scalar a funcțiilor care posedă o astfel de proprietate o conservă. Prin urmare, mulțimea acestor funcții este spațiu vectorial. Ele sunt studiate în detaliu, folosind metodele de analiză funcțională. Constrângerile algebrice produc și ele spații vectoriale: spațiul vectorial F[x]^⁠(d) este dat de polinoamele:

f(x) = r₀ + r₁x + ... + r_n-1x^n-1 + r_nxⁿ, unde coeficienții r₀, ..., r_n sunt în F.

Ecuații liniare

Sistemele de ecuații liniare omogene sunt strâns legate de spațiile vectoriale. De exemplu, soluțiile sistemului

a	+	3b	+	c	= 0
4a	+	2b	+	2c	= 0

sunt date de triplete arbitrare cu a, b = a/2 și c = −5a/2. Ele formează un spațiu vectorial: și după adunarea și înmulțirea cu un scalar a acestui gen de triplete, ele continuă să satisfacă aceleași raporturi dintre cele trei variabile; astfel și ele sunt soluții. Matricele pot fi folosite pentru a condensa mai multe ecuații liniare ca mai sus într-o singură ecuație vectorială, și anume:

Ax = 0,

unde A = ${\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}$ este matricea care conține coeficienții ecuațiilor date, x este vectorul (a, b, c), Ax reprezintă înmulțirea de matrice, și 0 = (0, 0) este vectorul zero. În mod similar, soluții ecuațiilor diferențiale liniare formează spații vectoriale. De exemplu,

f"(x) + 2f'(x) + f(x) = 0

produce f(x) = a e^−x + bx e^−x, unde a și b sunt constante arbitrare, și e^x e funcția exponențială cu baza naturală.

Baza și dimensiunea

Un vector v în R² (albastru) exprimat în termeni de baze diferite: folosind baza standard din R² v = xe₁ + ye₂ (negru), și folosind altă bază, neortogonală: v = f₁ + f₂ (roșu).

Bazele permit reprezentarea vectorilor cu ajutorul unui șir de scalari numit coordonate sau componente. O bază este o mulțime (finită sau infinită) B = {b_i}_{i ∈ I} de vectori b_am, pentru comoditate de multe ori indexați cu un indice^⁠(d) i, care generează întregul spațiu și este liniar independentă. „Care generează întregul spațiu” înseamnă că orice vector v poate fi exprimat ca sumă finită (numită combinație liniară) a elementelor bazei: $\mathbf {v} =a_{1}\mathbf {b} _{i_{1}}+a_{2}\mathbf {b} _{i_{2}}+\cdots +a_{n}\mathbf {b} _{i_{n}},$ unde a_k sunt scalari, numiți coordonatele (sau componentele) vectorului v în raport cu baza B, iar b_ik (k = 1, ..., n) elemente din B. Independența liniară înseamnă că coordonatele a_k sunt unic determinate pentru orice vector din spațiul vectorial.

De exemplu, versorii e₁ = (1, 0, ..., 0), e₂ = (0, 1, 0, ..., 0), până la e_n = (0, 0, ..., 0, 1), formează o bază în Kⁿ, numit bază canonică^⁠(d), deoarece orice vector (x₁, x₂, ..., x_n) poate fi exprimat unic ca o combinație liniară a acestor vectori:

(x₁, x₂, ..., x_n) = x₁(1, 0, ..., 0) + x₂(0, 1, 0, ..., 0) + ... + x_n(0, ..., 0, 1) = x₁e₁ + x₂e₂ + ... + x_ne_n.

Coordonatele corespunzătoare x₁, x₂, ..., x_n sunt coordonatele carteziene ale vectorului.

Fiecare spațiu vectorial are o bază. Acest lucru rezultă din lema lui Zorn, o formulare echivalentă a axiomei alegerii. Date fiind celelalte axiome ale teoriei mulțimilor Zermelo–Fraenkel, existența bazelor este echivalentă cu axioma alegerii. Teorema idealului prim^⁠(d), care este mai slabă decât axioma alegerii, implică faptul că toate bazele unui anumit spațiu vectorial au același număr de elemente, sau același cardinal^⁠(d) (cf. teorema dimensiunii spațiilor vectoriale^⁠(d)). Acest cardinal se numește dimensiunea spațiului vectorial, notată dim V. Dacă spațiul este generat de un număr finit de vectori, afirmațiile de mai sus pot fi demonstrate fără o astfel de informație fundamentală din teoria mulțimilor.

Dimensiunea de spațiului de coordonate Kⁿ este n, conform bazei expuse mai sus. Dimensiunea inelului polinomial F[x] introdus mai sus este infinit numărabilă, o bază fiind dată de 1, x, x², ... a fortiori^⁠(d), dimensiunea spațiilor mai generale de funcții, cum ar fi spațiul funcțiilor pe un interval (mărginit sau nemărginit), este infinită. Sub ipoteze potrivite de regularitate a coeficienților implicați, dimensiunea spațiului soluției unei ecuații diferențiale ordinare omogene este egal cu gradul ecuației. De exemplu, spațiul soluțiilor ecuației de mai sus este generat de e^−x și xe^−x. Aceste două funcții sunt liniar independente peste R, astfel încât dimensiunea acestui spațiu este doi, atât cât este și gradul ecuației.

O extindere de corp peste mulțimea numerelor raționale Q poate fi gândită ca spațiu vectorial peste Q (prin definirea adunării vectoriale ca adunarea corpului, definirea înmulțirii scalarilor ca fiind înmulțirea cu elemente din Q, și altfel ignorând înmulțirea corpului). Dimensiunea (sau gradul) de extinderii de domeniu Q(α) peste Q depinde de α. Dacă α satisface o ecuație polinomială

q_nαⁿ + q_n-1α^n-1 + ... + q₀ = 0, cu coeficienți raționali q_n, ..., q₀.

(„α este algebric”), dimensiunea este finită. Mai exact, este egală cu gradul polinomului minimal având α ca rădăcină. De exemplu, numerele complexe C formează un spațiu vectorial bidimensional real, generat de baza formată din 1 și unitatea imaginară i. Acesta îndeplinește condiția i² + 1 = 0, ecuație de gradul doi. Astfel, C este R-spațiu vectorial bidimensional (și, ca și orice corp comutativ, unidimensional ca spațiu vectorial peste el însuși, C). Dacă α nu este algebric, dimensiunea Q(α) peste Q este infinită. De exemplu, pentru α = π nu există nici o astfel de ecuație, cu alte cuvinte π este transcendent.

Aplicații liniare și matrice

Relația dintre două spații vectoriale poate fi exprimată printr-o aplicație liniară sau transformare liniară. Acestea sunt funcții care reflectă structura spațiului vectorial, adică ele conservă sumele și înmulțirea cu un scalar:

f(x + y) = f(x) + f(y) și f(a · x) = a · f(x) pentru orice x și y din V, orice a din K.

Un izomorfism este o aplicație liniară f : V → W astfel încât există o aplicație inversă g : W → V, cu proprietatea că cele două compuneri^⁠(d) posibile f ∘ g : W → W și g ∘ f : V → V sunt egale cu aplicația identitate. Echivalent, f este atât injectivă cât și surjectivă. Dacă există un izomorfism între V și W, se spune că cele două spații sunt izomorfe; acestea sunt, în esență, identice ca spații vectoriale, deoarece toate identitățile valabile în V sunt, prin intermediul lui f, transformate în altele similare în W, și vice-versa prin g.

Descrierea unui vector săgeată v prin coordonatele sale x și y dă un izomorfism de spații vectoriale.

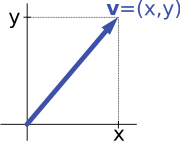
De exemplu, spațiile vectoriale „săgeți în plan” și „perechi ordonate de numere” din introducere sunt izomorfe: o săgeată în plan v care pornește din originea unui sistem de coordonate (fix) poate fi exprimată ca o pereche ordonată considerând componentele x și y ale săgeții, așa cum se arată în imaginea din dreapta. Analog, având în vedere o pereche (x, y), săgeata care duce x spre dreapta (sau spre stânga, dacă x este negativ), și y în sus (sau în jos, dacă y este negativ) se transformă înapoi în săgeata v.

Aplicațiile liniare V → W între două spații vectoriale formează un spațiu vectorial Hom_F(V, W),  notat și cu L(V, W). Spațiul aplicațiilor liniare de la V la K se numește spațiul vectorial dual^⁠(d), notat cu V^*. Prin intermediul aplicației injective naturale^⁠(d) V → V^∗∗, orice spațiu vectorial poate fi încorporat în bidualul său; aplicația este un izomorfism dacă și numai dacă spațiul este finit-dimensional.

Odată fiind aleasă o bază a lui V, aplicațiile liniare f : V → W sunt complet determinate prin specificarea imaginilor vectorilor din bază, deoarece orice element din V se exprimă în mod unic ca o combinație liniară a acestora. Dacă dim V = dim W, o corespondență 1-la-1 între bazele fixe ale lui V și W dă naștere la o aplicație liniară care mapează orice element din baza lui V cu un element corespunzător din baza lui W. Este un izomorfism, prin definiție. Prin urmare, două spații vectoriale sunt izomorfe dacă au aceeași dimensiune și vice-versa. Un alt mod de a exprima acest lucru este că orice spațiu vectorial este complet clasificat (până la izomorfism) de dimensiunea acestuia, un singur număr. În special, orice K-spațiu vectorial V n-dimensional este izomorf cu Kⁿ. Cu toate acestea, nu există un izomorfism „canonic” sau preferat; de fapt un izomorfism φ : Kⁿ → V este echivalent cu alegerea unei baze a lui V, mapând baza standard a lui Kⁿ cu V, prin intermediul lui φ. Libertatea de a alege o bază convenabilă este deosebit de utilă în context infinit-dimensional.

Matrice

O matrice tipică

Matricele sunt o noțiune utilă pentru codificarea aplicațiilor liniare. Ele sunt scrise ca un tablou dreptunghiular de scalari ca în imaginea din dreapta. Orice matrice m-pe-n A dă naștere unei aplicații liniare de la Kⁿ la K^m, cu următoarea lege:

$\mathbf {x} =(x_{1},x_{2},\cdots ,x_{n})\mapsto \left(\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\cdots ,\sum _{j=1}^{n}a_{mj}x_{j}\right)$, unde cu $\sum$ se notează suma,

sau, folosind înmulțirea matriceală a lui A cu coordonatele vectorului x:

x ↦ Ax.

Mai mult decât atât, după alegerea bazelor lui V și W, orice aplicație liniară f : V → W este unic reprezentată de o matrice prin această atribuire.

Volumul acestui paralelipiped este valoarea absolută a determinantului matricei 3-pe-3 formată din vectorii r₁, r₂și r₃.

Determinantul det(A) al unei matrice pătrate A este un scalar care spune dacă aplicația liniară asociată este un izomorfism sau nu: pentru a fi izomorfism, este suficient și necesar ca determinantul să fie nenul. Transformarea liniară a lui Rⁿ corespunzătoare unei matrice reale n-pe-n conservă orientarea^⁠(d) dacă și numai dacă determinantul este pozitiv.

Vectori și valori proprii

Endomorfismele^⁠(d), aplicații liniare f : V → V, sunt deosebit de importante deoarece, în acest caz, vectorii v pot fi comparați cu imaginea lor în raport cu f, f(v). Orice vector nenul v care satisface λv = f(v), unde λ este un scalar, se numește vector propriu al lui f cu valoarea proprie λ. Echivalent, v este un element al nucleului diferenței f − λ · Id (în cazul în care Id este aplicația identitate V → V). Dacă V este finit dimensional, acest lucru poate fi reformulat folosind determinanți: f având valoarea proprie λ este echivalent cu

det(f − λ · Id) = 0.

Dezvoltând definiția determinantului, expresia din partea stângă poate fi considerată a fi o funcție polinomială în λ, numită polinom caracteristic^⁠(d) al f. Dacă F este suficient de mare pentru a conține o rădăcină a acestui polinom (care în mod automat se întâmplă pentru F algebric închis, cum este K = C) orice aplicație liniară are cel puțin un vector propriu. Spațiul vectorial V poate sau nu să posede o bază proprie, bază formată din vectori proprii. Acest fenomen este guvernat de forma canonică Jordan^⁠(d) a aplicației. Mulțimea tuturor vectorilor proprii corespunzători unei anumite valori proprii a lui f formează un spațiu vectorial cunoscut ca spațiul vectorial propriu corespunzătoare valorii proprii (și lui f) în cauză. Pentru a ajunge la teorema spectrală^⁠(d), afirmația corespunzătoare în cazul infinit-dimensional, este nevoie de mecanismele analizei funcționale.

Construcția bazelor

În plus față de exemplele concrete de mai sus, există mai multe construcții liniare algebrice standard care generează spații vectoriale legate de cele date. În plus față de definițiile prezentate mai jos, acestea sunt și ele caracterizate prin proprietăți universale^⁠(d), care determină un obiect X prin specificarea aplicațiilor liniare de la X la orice alt spațiu vectorial.

Subspații și spații factor

O dreaptă care trece prin origine (albastru, gros) în R³ este un subspațiu liniar. Este intersecția a două planuri (verde și galben).

O submulțime nevidă W a unui spațiu vectorial V , care este închisă în raport cu adunarea și cu înmulțirea cu un scalar (și, prin urmare, conține vectorul zero din V) se numește subspațiu vectorial al lui V, sau pur și simplu subspațiu al lui V, atunci când spațiul ambiental este fără echivoc spațiu vectorial. Subspațiile lui V sunt spații vectoriale (peste același corp) de sine stătătoare. Intersecția tuturor subspațiilor conține o anumită mulțime S de vectori numită generatoare^⁠(d), și acesta este cel mai mic subspațiu al lui V care conține mulțimea S. Exprimat în termeni de elemente, generatoarea este subspațiul format din toate combinațiile liniare^⁠(d) de elemente din S.

Un subspațiu liniar de dimensiune 1 este o dreaptă vectorială. Un subspațiu liniar de dimensiune 2 este un plan de vectori. Un subspațiu liniar care conține toate elementele de bază din spațiul ambiental este un hiperplan de vectori. Într-un spațiu vectorial de dimensiune finită n, un hiperplan este astfel un subspațiu de dimensiune n – 1.

Omologul subspațiilor este spațiul vectorial factor. Dat fiind orice subspațiu W ⊂ V, spațiul factor V/W ("V modulo^⁠(d) W") este definit după cum urmează: ca mulțime, el se compune din v + W = {v + w : w ∈ W}, unde v este un vector arbitrar din V. Suma a două astfel de elemente v₁ + W și v₂ + W este (v₁ + v₂) + W, și înmulțirea cu un scalar este dată de un · (v + W) = (o · v) + W. Punctul cheie în această definiție este faptul că v₁ + W = v₂ + W dacă și numai dacă diferența dintre v₁ și v₂ se află în W. Astfel, spațiul factor „uită” informațiile conținute în subspațiul W.

Nucleul ker(f) unei aplicații liniare f : V → W este format din vectorii v care sunt mapați la 0 din W. Atât nucleul cât și imaginea im(f) = {f(v) : v ∈ V} sunt subspații ale lui V și, respectiv, W. Existența nucleelor și imaginilor face parte din afirmația că categoria spațiilor vectoriale^⁠(d) (peste un corp comutativ fix K) este categorie abeliană^⁠(d), adică un grup de obiecte matematice și aplicații de la una la alta care conservă structura (o categorie), care se comportă ca și categoria grupurilor abeliene^⁠(d). De aceea, multe afirmații, cum ar fi prima teoremă de izomorfism^⁠(d) (numită și teorema rangului^⁠(d) în termeni de matrice)

V / ker(f) ≡ im(f).

și a doua și a treia teoremă de izomorfism pot fi formulate și demonstrate într-un mod foarte similar cu situațiile corespunzătoare pentru grupuri.

Un exemplu important este nucleul unei aplicații liniare x ↦ Ax pentru o matrice fixă A, ca mai sus. Nucleul aceastei aplicații este un subspațiu de vectori x, astfel încât Ax = 0, care este tocmai mulțimea soluțiilor sistemului omogen de ecuații liniare care aparțin lui A. De asemenea, acest concept se extinde la ecuații diferențiale liniare

$a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0$, unde coeficienții a_i sunt și ei funcții de x.

În aplicația corespunzătoare

$f\mapsto D(f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}}$,

derivatele funcției f apar liniar (adică nu apar de exemplu sub forma de f''(x)²). Când diferențierea este o procedură liniară (adică (f + g)' = f' + g ' și (c·f)' = c·f' pentru orice constantă c) această atribuire este liniară, și se numește operator diferențial liniar^⁠(d). În particular, soluțiile ecuației diferențiale D(f) = 0 formează un spațiu vectorial (peste R sau C).

Produsul direct și suma directă

Produsul direct al unor spații vectoriale și suma directă a unor spații vectoriale sunt două moduri de a combina o familie indexată de spații vectoriale într-un nou spațiu vectorial.

Produsul direct $\textstyle {\prod _{i\in I}V_{i}}$ al unei familii de spații vectoriale v_i constă din mulțimea tuturor tuplurilor (v_i)_{i ∈ I}, care specifică pentru fiecare indice i dintr-o mulțime de indici^⁠(d) I un element v_i al lui V_i. Adunarea și înmulțirea cu un scalar se realizează pe componente. O variantă a acestei construcții este suma directă $\oplus _{i\in I}V_{i}$ (notată cu $\textstyle {\coprod _{i\in I}V_{i}}$), în care sunt permise numai tuplurile cu un număr finit de vectori nenuli. Dacă mulțimea de indici I este finită, cele două construcții sunt în acord, dar, în general, ele sunt diferite.

Produsul tensorial

Produsul tensorial V ⊗_F W, sau mai simplu V ⊗ W, a două spații vectoriale V și W este una dintre noțiunile centrale ale algebrei multiliniare^⁠(d) care se ocupă cu extinderea noțiunilor cum ar fi aplicațiile liniare la mai multe variabile. O aplicație g : V × W → X se numește biliniară dacă g este liniară în ambele variabile v și w. Cu alte cuvinte, pentru un w fix, aplicația v ↦ g(v, w) este liniară în sensul de mai sus și analog pentru v fix.

Produsul tensorial este un anumit spațiu vectorial care este primitor universal al aplicațiilor biliniare g, după cum urmează. Este definit ca spațiu vectorial format din sume finite (formale) de simboluri numite tensori

v₁ ⊗ w₁ + v₂ ⊗ w₂ + ... + v_n ⊗ w_n,

supuse regulilor

a · (v ⊗ w) = (a · v) ⊗ w = v ⊗ (a · w), unde a este un scalar,

(v₁ + v₂) ⊗ w = v₁ ⊗ w + v₂ ⊗ w, și

v ⊗ (w₁ + w₂) = v ⊗ w₁ + v ⊗ w₂.

Diagrama comutativă^⁠(d) reprezentând proprietatea universală a produsului tensorial.

Aceste reguli asigură că aplicația f definită pe V × W cu valori în V ⊗ W care mapează un tuplu^⁠(d) (v, w) în v ⊗ w este biliniară. Universalitatea afirmă că, dat fiind orice spațiu vectorial X și orice aplicație biliniară g : V × W → X, există o aplicație unică u, arătată în diagramă cu o săgeată punctată, a cărei compoziție^⁠(d) cu f este egală cu g: u(v ⊗ w) = g(v, w). Aceasta se numește proprietatea universală^⁠(d) a produsului tensorial, un exemplu de metodă mult utilizată în algebra abstractă avansată—pentru a defini indirect obiecte prin specificarea unor aplicații definite pe acel obiect sau cu valori în el.

Spații vectoriale cu structură suplimentară

Din punctul de vedere al algebrei liniare, spațiile vectoriale sunt complet înțelese în măsura în care orice spațiu vectorial este caracterizat, până la izomorfism, prin dimensiunea sa. Cu toate acestea, spațiile vectoriale în sine nu oferă un cadru de abordare a chestiunii—cruciale pentru analiză—dacă un șir de funcții converge către o altă funcție. De asemenea, algebra liniară nu este adaptată pentru a trata șiruri infinite, deoarece operația aditivă permite adunarea numai a unui număr finit de termeni. Prin urmare, nevoile analizei funcționale impun considerarea unor structuri suplimentare.

Unui spațiu vectorial i se poate da o relație de ordine parțială ≤, în care unii vectori pot fi comparați. De exemplu, spațiul n-dimensional real Rⁿ poate fi ordonat prin compararea vectorilor pe componente. Spațiile vectoriale ordonate^⁠(d), cum ar fi spațiile Riesz^⁠(d), sunt fundamentale pentru integrarea Lebesgue^⁠(d), care se bazează pe capacitatea de a exprima o funcție ca o diferență de două funcții pozitive

f = f⁺ − f⁻,

unde f⁺ reprezintă partea pozitivă a lui f și f⁻ partea negativă.

Spații vectoriale normate și spații cu produs scalar

„Măsurarea” vectorilor se face prin specificarea unei norme, un datum care măsoară lungimi de vectori, sau printr-un produs scalar, care măsoară unghiurile dintre vectori. Normele și produsele scalare se notează cu $|\mathbf {v} |$ și, respectiv, cu $\langle \mathbf {v} ,\mathbf {w} \rangle$. Natura unui produs scalar presupune că lungimile de vectori pot fi și ele definite, prin definirea normei asociate $|\mathbf {v} |:={\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}$. Spațiile vectoriale înzestrate cu astfel de date sunt cunoscute sub denumirea de spații vectoriale normate și, respectiv, spații prehilbertiene.

Coordonatele spațiului Kⁿ pot fi echipate cu produsul scalar standard:

$\langle \mathbf {x} ,\mathbf {y} \rangle =\mathbf {x} \cdot \mathbf {y} =x_{1}y_{1}+\cdots +x_{n}y_{n}.$

În R², acest lucru reflectă noțiunea comună de unghi între doi vectori x și y, prin legea cosinusurilor:

$\mathbf {x} \cdot \mathbf {y} =\cos \left(\angle (\mathbf {x} ,\mathbf {y} )\right)\cdot |\mathbf {x} |\cdot |\mathbf {y} |.$

Din această cauză, doi vectori care satisfac relația $\langle \mathbf {x} ,\mathbf {y} \rangle =0$ se numesc ortogonali. O variantă importantă a produsului scalar standard este folosită în spațiul Minkowski: R⁴ înzestrat cu produsul Lorentz

$\langle \mathbf {x} |\mathbf {y} \rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}.$

Spre deosebire de produsul scalar standard, acesta nu este pozitiv definit^⁠(d): $\langle \mathbf {x} |\mathbf {x} \rangle$ ia și valori negative, de exemplu pentru $\mathbf {x} =(0,0,0,1)$. Izolarea celei de-a patra coordonate corespunzătoare timpului, spre deosebire de cele trei dimensiuni ale spațiului—îl face util pentru tratarea matematică a relativității restrânse.

Spatii vectoriale topologice

Chestiunile de convergență sunt tratate prin luarea în considerare a spațiilor vectoriale V care au și o topologie compatibilă, o structură care ne permite să vorbim despre elemente ca fiind aproape unul de altul. „Compatibil” aici înseamnă că, adunarea și înmulțirea cu un scalar trebuie să fie aplicații continue. Aproximativ, dacă x și y din V, și a din K variază cu o cantitate mărginită, atunci la fel variază și x + y și ax. Pentru a avea sens precizarea cantității cu care se modifică un scalar, corpul K trebuie să aibă în acest context și o topologie; o alegere comună sunt numerele reale sau cele complexe.

În astfel de spații vectoriale topologice, se poate considera un șir de vectori. Suma infinită

$\sum _{i=0}^{\infty }f_{i}$

reprezintă limita sumelor parțiale finite ale șirului (f_i)_i∈N de elemente din V. De exemplu, f_i ar putea fi funcții (reale sau complexe) aparținând unui spațiu funcțional V, caz în care seria este o serie de funcții^⁠(d). Modul de convergență^⁠(d) al seriei depinde de topologia impusă spațiului de funcții. În astfel de cazuri, convergența punctuală și convergența uniformă^⁠(d) sunt două exemple elocvente.

„Sferele” unitate din R² constau din vectori plani de normă 1. Sunt ilustrate sferele unitate în diferite p-norme, pentru p = 1, 2, și ∞. Pătratul cel mare ilustrează punctele a căror 1-normă este egală cu 2.

O modalitate de a asigura existența unor limite ale anumitor serii infinite este de a restricționa atenția asupra spațiilor în care orice șir Cauchy este convergent; un astfel de spațiu vectorial se numește complet. Aproximativ, un spațiu vectorial este complet cu condiția ca acesta să conțină toate limitele necesare. De exemplu, spațiul vectorial al polinoamelor definite pe intervalul unitate [0,1], echipat cu topologia convergenței uniforme^⁠(d) nu este complet, deoarece orice funcție continuă pe [0,1] poate fi uniform aproximată printr-un șir de polinoame, de către teorema de aproximare Weierstrass^⁠(d). În schimb, spațiul tuturor funcțiilor continue pe [0,1] cu aceeași topologie este complet. O normă dă naștere unei topologii prin definirea noțiunii că un șir de vectori v_n converge în v dacă și numai dacă

${\text{lim}}_{n\rightarrow \infty }|\mathbf {v} _{n}-\mathbf {v} |=0.$

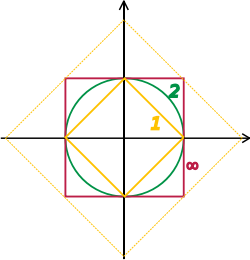
Spațiile Banach și Hilbert sunt spații vectoriale topologice complete ale căror topologii sunt date de o normă și, respectiv, de un produs scalar. Studiul lor—o piesă-cheie în analiza funcțională—se axează pe spații vectoriale infinit-dimensionale, deoarece toate normele pe spații vectoriale topologice finit-dimensionale dau naștere la aceeași noțiune de convergență. Imaginea din dreapta arată echivalența 1-normei și ∞-normei pe R²: cum „bilele” unitate se includ una pe alta, un șir converge la zero într-una din norme, dacă și numai dacă el converge și în cealaltă. În cazul infinit-dimensional însă vor exista, în general, topologii neechivalente, care fac studiul spațiilor vectoriale topologice mai bogat decât cel al spațiilor vectoriale fără date suplimentare.

Din punct de vedere conceptual, toate noțiunile legate de spații vectoriale topologice ar trebui să se potrivească cu topologia. De exemplu, în loc de a considera toate aplicațiile liniare (denumite și funcționale^⁠(d)) V → W, aplicațiile între spații vectoriale topologice sunt obligate să fie continue. În special, spațiul dual (topologic) V^∗ constă din funcționale continue V → R (sau C). Teorema fundamentală Hahn–Banach^⁠(d) tratează separarea subspațiilor corespunzătoare spațiilor vectoriale topologice de funcționalele continue.

Spații Banach

Spațiile Banach, prezentate de Stefan Banach, sunt spații vectoriale complete normate. Un prim exemplu este spațiul vectorial ℓ ^p constând din vectori infiniți cu elemente reale x = (x₁, x₂, ...) ale căror p-norme (1 ≤ p ≤ ∞) date de

$|\mathbf {x} |_{p}:=\left(\sum _{i}|x_{i}|^{p}\right)^{1/p}$ pentru p < ∞ și $|\mathbf {x} |_{\infty }:={\text{sup}}_{i}|x_{i}|$

sunt finite. Topologiile pe spațiul infinit-dimensional ℓ ^p sunt neechivalente pentru p diferite. De exemplu, șirul de vectori x_n = (2⁻ⁿ, 2⁻ⁿ, ..., 2⁻ⁿ, 0, 0, ...), adică primele 2ⁿ cu valoarea 2⁻ⁿ, și următoarele 0, converge la vectorul nul pentru p = ∞, dar nu și pentru p = 1:

$|x_{n}|_{\infty }=\sup(2^{-n},0)=2^{-n}\rightarrow 0$, dar $|x_{n}|_{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1.$

Mai general decât șirurile de numere reale, funcțiile f: Ω → R sunt dotate cu o normă care înlocuiește suma de mai sus cu integrala Lebesgue^⁠(d)

$|f|_{p}:=\left(\int _{\Omega }|f(x)|^{p}\,dx\right)^{1/p}.$

Spațiul funcțiilor integrabile pe un anumit domeniu Ω (de exemplu un interval) care satisfac | f |_p < ∞, și sunt echipate cu această normă se numesc spații Lebesgue, notate L^p(Ω). Aceste spații sunt complete. (Dacă se folosește integrala Riemann în schimb, spațiul nu este complet, ceea ce poate fi considerat a fi o justificare pentru teoria integrării Lebesgue.) Concret, aceasta înseamnă că pentru orice șir de funcții integrabile Lebesgue f₁, f₂, ... , cu | f_n |_p < ∞, care îndeplinesc condiția

$\lim _{k,\ n\to \infty }\int _{\Omega }|{f}_{k}(x)-{f}_{n}(x)|^{p}\,dx=0$

există o funcție f(x) aparținând spațiului vectorial L^p(Ω), astfel încât

$\lim _{k\to \infty }\int _{\Omega }|{f}(x)-{f}_{k}(x)|^{p}\,dx=0.\$

Impunerea condițiilor de mărginire nu numai pe funcție, ci și pe derivatele ei, duce la spații Sobolev^⁠(d).

Spații Hilbert

Cadrele succesive arată însumarea a de la 1 la 5 termeni care aproximează o funcție periodică (albastru) cu o sumă finită de funcții sinusoidale (roșu).

Spațiile prehilbertiene complete se numesc spații Hilbert, în cinstea lui David Hilbert. În spațiul Hilbert L²(Ω), cu produsul scalar dat de

$\langle f\ ,\ g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\,dx,\,\!$

unde cu ${\overline {g(x)}}$ se notează conjugata complexă a lui g(x), este un caz-cheie.

Prin definiție, într-un spațiu Hilbert, orice șir Cauchy converge la o limită. În schimb, este la fel de importantă și găsirea unui șir de funcții f_n cu proprietățile dorite care aproximează o anumită funcție-limită. Analiza timpurie, sub forma aproximării Taylor, a stabilit o aproximare a funcțiilor derivabile f cu polinoame. Conform teoremei Stone–Weierstrass^⁠(d), orice funcție continuă pe [a, b] poate fi aproximată oricât de îndeaproape se dorește cu un polinom. O tehnică similară de aproximare cu funcții trigonometrice se numește de obicei dezvoltare în serie Fourier, și este aplicată frecvent în inginerie, a se vedea mai jos. Mai general, și mai conceptual, teorema dă o simplă descriere a ce „funcții de bază”, sau, în spațiile Hilbert abstracte, a ce vectori din bază sunt suficienți pentru a genera un spațiu Hilbert H, în sensul că închiderea^⁠(d) intervalului generat de ele (de exemplu, combinațiile liniare finite și limitele acestora) este întregul spațiu. O astfel de mulțime de funcții se numește o bază a lui H, cardinalitatea sa fiind cunoscută ca dimensiune a spațiului Hilbert. Nu numai că teorema prezintă funcțiile corespunzătoare din bază ca fiind suficiente pentru scopul aproximării, ci, împreună cu procedeul Gram-Schmidt, ea permite și construirea unei baze de vectori ortogonali^⁠(d). Astfel de baze ortogonale sunt generalizările la nivel de spațiu Hilbert ale axelor de coordonate în spațiul euclidian finit-dimensional.

Soluțiile a diverse ecuații diferențiale pot fi interpretate în termeni de spații Hilbert. De exemplu, numeroase domenii ale fizicii și ingineriei duc la astfel de ecuații și soluții cu anumite proprietăți fizice sunt frecvent utilizate ca funcții de bază, de multe ori ortogonale. Ca un exemplu din fizică, ecuația lui Schrödinger dependentă de timp din mecanica cuantică descrie schimbarea proprietăților fizice în timp printr-o ecuație cu derivate parțiale, ale cărei soluții sunt numite funcții de undă. Valorile definite pentru proprietățile fizice, cum ar fi energia, sau impulsul, corespund valorilor proprii ale unui operator diferențial^⁠(d) (liniar) și funcțiile de undă asociate se numesc stări proprii. Teorema spectrală^⁠(d) descompune un operator compact^⁠(d) liniar care acționează asupra funcțiilor în termenii acestor funcții proprii și valorilor lor proprii.

Algebre peste corpuri

O hiperbolă, dată de ecuația x ⋅ y = 1. Inelul de coordonate^⁠(d) al funcțiilor pe această hiperbolă este dat de R[x, y] / (x · y − 1), un spațiu vectorial infinit-dimensional peste R.

Spațiile vectoriale generale nu posedă o înmulțire între vectori. Un spațiu vectorial dotat un operator biliniar care definește înmulțirea a doi vectori este o algebră peste un corp. Multe algebre rezultă din funcții definite pe unele obiecte geometrice: întrucât funcțiile cu valori într-un anumit domeniu pot fi înmulțite punctual, aceste entități formează algebre. Teorema Stone–Weierstrass menționată mai sus, de exemplu, se bazează pe algebre Banach^⁠(d), care sunt atât spații Banach, cât și algebre.

Algebra comutativă face mare uz de inele de polinoame^⁠(d) într-una sau mai multe variabile, introduse mai sus. Înmulțirea lor este atât comutativă, cât și asociativă. Aceste inele și factorii lor formează baza geometriei algebrice, deoarece acestea sunt inele de funcții de obiecte geometrice algebrice^⁠(d).

Un alt important exemplu sunt algebrele Lie, care nu sunt nici comutative și nici asociative, dar faptul că nu sunt limitate de constrângerile ([x, y] reprezintă produsul dintre x și y):

• [x, y] = −[y, x] (anticomutativitate^⁠(d)), și
• [x, [y, z]] + [y, [z, x]] + [z, [x, y]] = 0 (identitatea Jacobi^⁠(d)).

Printre exemple se numără spațiul vectorial al matricelor n-pe-n, cu [x, y] = xy − yx, comutatorul^⁠(d) a două matrice, și R³, dotat cu produsul vectorial.

Algebra tensorială^⁠(d) T(V) este un mod formal de a adăuga produsul la orice spațiu vectorial V pentru a obține o algebră. Ca spațiu vectorial, este generat de simboluri, numite simplu tensori

v₁ ⊗ v₂ ⊗ ... ⊗ v_n, unde gradul n variază.

Înmulțirea este dată prin concatenarea acestor simboluri, care impune în plus legea distributivă față de adunare, și faptul că necesită ca înmulțirea cu un scalar să fie comutativă cu produsul tensorial ⊗, în același fel ca și produsul tensorial a două spații vectoriale introdus mai sus. În general, nu există relații între v₁ ⊗ v₂ și v₂ ⊗ v₁. Forțând două astfel de elemente să fie egale, se obțin algebre simetrice^⁠(d), pe când punerea condiției ca v₁ ⊗ v₂ = − v₂ ⊗ v₁ dă algebre exterioare.

Aplicații

Spații vectoriale au multiple aplicații întrucât apar în multe situații, și anume oriunde sunt implicate funcții cu valori într-un anumit corp. Ele oferă un cadru de tratare a problemelor analitice și geometrice, sau sunt utilizate în transformata Fourier. Această listă nu este exhaustivă: există mult mai multe aplicații, de exemplu, în optimizare. Teorema minimax^⁠(d) din teoria jocurilor, care afirmă existența unui câștig unic atunci când toți jucătorii joacă optim poate fi formulată și demonstrată folosind metode cu spații vectoriale. Teoria reprezentării reușește să transfere buna înțelegere a algebrei liniare și a spațiilor vectoriale în alte domenii matematice, cum ar fi teoria grupurilor.

Distribuții

O distribuție (sau o funcție generalizată) este o aplicație liniară ce atribuie un număr fiecărei funcții „test”^⁠(d), de obicei, o funcție netedă^⁠(d) cu suport compact^⁠(d), într-un mod continuu: în terminologia de mai sus, spațiul distribuțiilor este dualul (continuu) al spațiului funcției „test”. Acesta din urmă este dotat cu o topologie care ia în considerare nu numai pe f în sine, ci și toate derivatele sale superioare. Un exemplu standard este rezultatul integrării unei funcții test f pe un domeniu Ω:

$I(f)=\int _{\Omega }f(x)\,dx.$

Atunci când Ω = {p}, mulțimea formată dintr-un singur punct, aceasta se reduce la distribuția Dirac, notată cu δ, care asociază unei funcții test f valoarea sa în punctul p: δ(f) = f(p). Distribuțiile sunt un instrument puternic de rezolvare a ecuațiilor diferențiale. Deoarece toate noțiunile analitice standard, cum ar fi derivatele, sunt liniare, ele se extind în mod natural în spațiul distribuțiilor. Prin urmare, ecuația în cauză poate fi transferată într-un spațiu de distribuție, care este mai mare decât spațiul funcțional de bază, astfel că sunt disponibile mai multe metode flexibile pentru rezolvarea ecuației. De exemplu, funcțiile lui Green^⁠(d) și soluțiile fundamentale^⁠(d) sunt, de obicei, distribuții, și nu funcții propriu-zise, și pot fi apoi folosite pentru a găsi soluții ale ecuației cu condițiile la limită prescrise. Soluția găsită poate fi atunci, în unele cazuri, demonstrată a fi de fapt o funcție adevărată, și o soluție pentru ecuația originală (de exemplu, folosind teorema Lax–Milgram^⁠(d), o consecință a teoremei de reprezentare Riesz^⁠(d)).

Analiza Fourier

Ecuația căldurii descrie variația proprietăților fizice în timp, cum ar fi scăderea temperaturii unui corp fierbinte plasat într-un mediu mai rece (galben descrie regiunile mai reci decât cele roșii).

Dezvoltarea unei funcții periodice într-o sumă de funcții trigonometrice formează o serie Fourier, o tehnică des utilizată în fizică și inginerie. Spațiul vectorial este, de obicei, spațiul Hilbert L²(0, 2π), pentru care funcțiile sin mx și cos mx (cu m un număr întreg) formează o bază ortogonală. Dezvoltarea în serie Fourier a unei funcții L²f este

${\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }\left[a_{m}\cos \left(mx\right)+b_{m}\sin \left(mx\right)\right].$

Coeficienții a_m și b_m se numesc coeficienții Fourier ai lui f, și sunt calculați prin formulele

$a_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\cos(mt)\,dt$, $b_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\sin(mt)\,dt.$

Din punct de vedere fizic, funcția este reprezentată ca o suprapunere de unde sinusoidale și coeficienții dau informații despre spectrul de frecvență^⁠(d) al funcției. Se mai folosește frecvent și o formă cu numere complexe a seriei Fourier. Formulele concrete de mai sus sunt consecințele unei mai generale dualități matematice numită dualitate Pontreaghin^⁠(d). Aplicată grupului R, ea dă transformata Fourier clasică; o aplicație în fizică sunt rețelele reciproce^⁠(d), în care grupul de bază este un spațiu vectorial finit-dimensional real înzestrat cu elementele suplimentare ale unei rețele ce codifică pozițiile atomilor în cristale.

Seriile Fourier sunt folosite și pentru a rezolva probleme ale valorilor limită^⁠(d) în ecuațiile cu derivate parțiale. În 1822, Fourier a fost primul care a folosit această tehnică pentru a rezolva ecuația căldurii^⁠(d). O versiune discretă a seriilor Fourier se poate folosi în aplicații de eșantionare în care valoarea funcției este cunoscută doar într-un număr finit de puncte echidistante. În acest caz, seria Fourier este finită și valoarea sa este peste tot egală cu punctele eșantionate. Mulțimea coeficienților este cunoscută sub numele de transformata Fourier discretă^⁠(d) (DFT) a eșantionului dat. DFT este unul dintre instrumentele-cheie din prelucrarea semnalelor digitale^⁠(d), un domeniu printre ale cărui aplicații se numără radarul, codificarea sunetului^⁠(d), compresia imaginilor. Formatul de imagine JPEG este o aplicație strâns legată de transformarea cosinus discretă.

Transformata Fourier rapidă^⁠(d) este un algoritm rapid de calcul a transformatei Fourier discrete. Este folosit nu numai pentru calculul coeficienților Fourier ci, folosind teorema de convoluție^⁠(d), și pentru calculul convoluției a două șiruri finite. Acestea, la rândul lor, sunt aplicate în filtrele digitale^⁠(d) și ca algoritm rapid de înmulțire^⁠(d) pentru polinoame și numere întregi mari (algoritmul Schönhage-Strassen^⁠(d)).

Geometrie diferențială

Spațiul tangent la o 2-sferă la un moment dat este planul infinit care atinge sfera în acel punct.

Planul tangent^⁠(d) la o suprafață într-un punct este, în mod natural, un spațiu vectorial a cărui origine este punctul de contact. Planul tangent este cea mai bună aproximare liniară, sau liniarizare^⁠(d) a unei suprafețe într-un punct. Chiar și într-un spațiu euclidian tridimensional, nu există de obicei niciun mod natural de a prescrie o bază a planului tangent, și, deci, el este conceput ca un spațiu vectorial abstract, mai degrabă decât ca un spațiu cu coordonate reale. Spațiul tangent este generalizarea la varietăți diferențiabile^⁠(d) de dimensiuni superioare.

Varietatile riemanniene^⁠(d) sunt varietăți ale căror spații tangente sunt dotate cu un produs scalar adecvat. De aici rezultă tensorul Riemann (de curbură) care codifică toate curburile unei varietăți într-un singur obiect, care își găsește aplicații în teoria relativității generale, de exemplu, în care tensorul Einstein^⁠(d) descrie materia și conținutul de energie al spațiu-timpului. Spațiul tangent la un grup Lie poate fi dat în mod natural ca structura unei algebre Lie și poate fi folosit pentru a clasifica grupuri Lie compacte^⁠(d).

Generalizări

Fibrate vectoriale

O bandă Möbius. La nivel local, ea seamănă cu^⁠(d) U × R.

Un fibrat vectorial este o familie de spații vectoriale parametrizate continuu de un spațiu topologic X. Mai precis, un fibrat vectorial peste X este un spațiu topologic E echipat cu o aplicație continuă

$\pi \colon E\rightarrow X$

cu proprietatea că pentru orice x din X, fibra^⁠(d) π^-1(x) este un spațiu vectorial. Cazul dim V = 1 se numește o fibră de drepte^⁠(d). Pentru orice spațiu vectorial V, proiecția X × V → X transformă produsul X × V într-un fibrat vectorial „trivial”^⁠(d). Fibratele vectoriale peste X sunt în mod necesar la nivel local^⁠(d) un produs între X și un spațiu vectorial fixat V: pentru fiecare x din X, există o vecinătate U a lui x astfel încât restricția lui π la π^-1(U) este izomorfă cu fibratul trivial U × V → U. În ciuda caracterului lor local și trivial, fibratele vectoriale pot (în funcție de forma spațiului-suport X) să fie „răsucite” la scară mare (de exemplu, fibratul nu trebuie să fie global izomorf cu fibratul trivial X × V). De exemplu, fâșia lui Möbius poate fi văzută ca un fibrat vectorial de drepte peste cercul S¹ (identificând intervale deschide pe dreapta reală). Cu toate acestea, este diferit de cilindrul S¹ × R, deoarece acesta din urmă este orientabil^⁠(d), în timp ce fâșia lui Möbius, nu.

Proprietățile anumitor fibrate vectoriale oferă informații despre spațiul topologic suport al lor. De exemplu, fibratul tangent^⁠(d) constă din mulțimea spațiilor tangente^⁠(d) parametrizată de punctele unei varietăți derivabile. Fibratul tangent la cercul S¹ la nivel global este izomorf cu S¹ × R, deoarece nu există câmp vectorial global nenul pe S¹. În contrast, conform teoremei bilei păroase^⁠(d), nu există niciun câmp vectorial (tangent) pe 2-sfera S², care să fie peste tot nenul. K-teoria^⁠(d) studiază clasele de izomorfism ale tuturor fibratelor vectoriale peste un spațiu topologic. În plus față de perspectivele topologice și geometrice mai profunde, conceptul are consecințe pur algebrice, cum ar fi clasificarea algebrelor cu diviziune reale și de dimensiuni finite: R, C, cuaternionii H și octonionii O.

Fibratul cotangent^⁠(d) al unei varietăți diferențiabile constă, în fiecare punct al varietății, din dualul spațiului tangent, spațiul cotangent^⁠(d). Secțiunile^⁠(d) acelui fibrat sunt cunoscute sub numele de 1-formă diferențială^⁠(d).

Module

Modulele sunt pentru inele ce sunt spații vectoriale pentru corpuri: aceleași axiome, aplicate la un inel I în loc de un corp comutativ K, dau module. Teoria modulelor, față de cea a spațiilor vectoriale, este complicată de prezența elementelor de inel care nu au element invers multiplicativ^⁠(d). De exemplu, modulele nu au neapărat baze, după cum demonstrează Z-modulul (de exemplu, grupul abelian) Z/2Z^⁠(d); acele module care au bază (între care se numără și spațiile vectoriale) sunt cunoscute sub numele de module libere^⁠(d). Cu toate acestea, un spațiu vectorial poate fi compact definit ca un modul^⁠(d) peste un inel care este și corp, elementele lui fiind denumite vectori. Unii autori folosesc termenul de spațiu vectorial cu sensul de modul peste un inel cu operație de diviziune. Interpretarea algebro-geometrică a inelelor comutative prin intermediul spectrului^⁠(d) permite dezvoltarea de concepte cum ar fi module local libere^⁠(d), omologul algebric al fibratelor vectoriale.

Spații afine și proiective

Un plan afin (albastru-deschis) în R³. Este un subspațiu bidimensional deplasat cu un vector x (roșu).

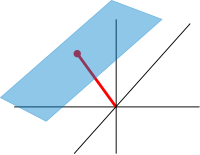
Ca definiție aproximativă, spațiile afine sunt spații vectoriale ale căror origini nu sunt specificate. Mai precis, un spațiu afin este o mulțime cu o acțiune de spațiu vectorial liber tranzitivă^⁠(d). În special, un spațiu vectorial este un spațiu afin peste sine, prin aplicația

V × V → V, (v, a) ↦ a + v.

Dacă W este un spațiu vectorial, atunci un subspațiu afin este o submulțime a lui G obținută prin translatarea unui subspatiu liniar V cu un vector x ∈ W fixat; acest spațiu este notat cu x + V și este format din toți vectorii de forma x + v pentru v ∈ V. Un exemplu important este spațiul soluțiilor unui sistem de ecuații liniare neomogene

Ax = b

generalizând cazul omogen b = 0 de mai sus. Spațiul soluțiilor este subspațiul afin x + V , unde x este o soluție particulară a ecuației, și V este spațiul de soluții ale ecuației omogene (nucleul lui A).

Mulțimea subspațiilor monodimensionale ale unui spațiu vectorial finit-dimensional V este cunoscută ca spațiu proiectiv; acesta poate fi folosit pentru a formaliza ideea dreptelor paralele care se intersectează la infinit. Grassmannienii^⁠(d) și varietățile de steaguri^⁠(d) generalizează acest lucru prin parametrizarea subspațiilor vectoriale de dimensiune fixă k și, respectiv, a steagurilor subspațiilor.

Bibliografie

Algebră

• Artin, Michael (1991), Algebra, Prentice Hall^⁠(d), ISBN 978-0-89871-510-1 
• Blass, Andreas (1984), „Existence of bases implies the axiom of choice”, Axiomatic set theory (Boulder, Colorado, 1983), Contemporary Mathematics, 31, Providence, R.I.: American Mathematical Society, pp. 31–33 
• Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5 
• Lang, Serge (1987), Linear algebra, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-96412-6 
• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (ed. Revised third), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556 
• Mac Lane, Saunders (1999), Algebra (ed. 3rd), pp. 193–222, ISBN 0-8218-1646-2 
• Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM^⁠(d), ISBN 978-0-89871-454-8 
• Roman, Steven (2005), Advanced Linear Algebra, Graduate Texts in Mathematics, 135 (ed. 2nd), Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-24766-3 
• Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, CRC, ISBN 978-0-8247-9144-5 
• van der Waerden, Bartel Leendert (1993), Algebra (în germană) (ed. 9), Berlin, New York: Springer Science+Business Media, ISBN 978-3-540-56799-8 

Analiză

• Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin, New York: Springer Science+Business Media, ISBN 978-3-540-13627-9 
• Bourbaki, Nicolas (2004), Integration I, Berlin, New York: Springer Science+Business Media, ISBN 978-3-540-41129-1 
• Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-97894-9 
• BSE-3 (2001), „Tangent plane”, În Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Choquet, Gustave (1966), Topology, Boston, MA: Academic Press^⁠(d) 
• Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, Courier Dover Publications, ISBN 978-0-486-69193-0 
• Dudley, Richard M. (1989), Real analysis and probability, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6 
• Dunham, William (2005), The Calculus Gallery, Princeton University Press, ISBN 978-0-691-09565-3 
• Evans, Lawrence C. (1998), Partial differential equations, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0772-9 
• Folland, Gerald B. (1992), Fourier Analysis and Its Applications, Brooks-Cole, ISBN 978-0-534-17094-3 
• Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 0-387-98485-2 
• Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (ed. 2nd), Harlow, Essex, England: Prentice-Hall (publicat la 2002), ISBN 0-201-59619-9 
• Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 0-88385-031-1 
• Kreyszig, Erwin (1988), Advanced Engineering Mathematics (ed. 6th), New York: John Wiley & Sons, ISBN 0-471-85824-2 
• Kreyszig, Erwin (1989), Introductory functional analysis with applications, Wiley Classics Library, New York: Wiley, ISBN 978-0-471-50459-7 
• Lang, Serge (1983), Real analysis, Addison-Wesley^⁠(d), ISBN 978-0-201-14179-5 
• Lang, Serge (1993), Real and functional analysis, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-94001-4 
• Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York–London: D. Van Nostrand Company, Inc., pp. x+190 
• Schaefer, Helmut H.; Wolff, M.P. (1999), Topological vector spaces (ed. 2nd), Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-98726-2 
• Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press^⁠(d) 

Referințe istorice

• Banach, Stefan (1922), „Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales” [Despre operațiunile din cadrul mulțimilor abstracte și aplicațiile lor în ecuații integrale] (PDF), Fundamenta Mathematicae^⁠(d) (în franceză), 3, ISSN 0016-2736 
• Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie [Considerațiuni asupra unor aspecte ale geometriei elementare] (în germană) 
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques [Elemente de istoria matematicii] (în franceză), Paris: Hermann 
• Dorier, Jean-Luc (1995), „A general outline of the genesis of vector space theory”, Historia Mathematica^⁠(d), 22 (3): 227–261, doi:10.1006/hmat.1995.1024 
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (în franceză), Chez Firmin Didot, père et fils 
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (în germană), O. Wigand , retipărit: Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Kannenberg, L.C., ed., Extension Theory, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5 
• Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy 
• Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie [Analiză baricentrică: un nou instrument de tratare analitică a geometriei] (în germană), arhivat din original la 23 noiembrie 2006, accesat în 13 septembrie 2016 
• Moore, Gregory H. (1995), „The axiomatization of linear algebra: 1875–1940”, Historia Mathematica^⁠(d), 22 (3): 262–303, doi:10.1006/hmat.1995.1025 
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (în italiană), Torino 

Alte referințe

• Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1 
• Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (ed. 2nd), Addison-Wesley^⁠(d), ISBN 978-0-201-09394-0 
• Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: Springer Science+Business Media, ISBN 978-3-540-64243-5 
• Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer Science+Business Media, ISBN 978-3-540-64241-1 
• Coxeter, Harold Scott MacDonald (1987), Projective Geometry (ed. 2nd), Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-96532-1 
• Eisenberg, Murray; Guy, Robert (1979), „A proof of the hairy ball theorem”, The American Mathematical Monthly^⁠(d), Mathematical Association of America, 86 (7): 572–574, doi:10.2307/2320587 
• Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-94269-8 
• Goldrei, Derek (1996), Classic Set Theory: A guided independent study (ed. 1st), London: Chapman and Hall^⁠(d), ISBN 0-412-60610-0 
• Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: Prentice Hall^⁠(d), ISBN 0-13-124405-1 
• Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-90093-3 
• Halpern, James D. (1966), „Bases in Vector Spaces and the Axiom of Choice”, Proceedings of the American Mathematical Society^⁠(d), American Mathematical Society, 17 (3): 670–673, doi:10.2307/2035388 
• Husemoller, Dale (1994), Fibre Bundles (ed. 3rd), Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-94087-8 
• Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (ed. 4th), Berlin, New York: Springer Science+Business Media, ISBN 978-3-540-25907-7 
• Kreyszig, Erwin (1991), Differential geometry, New York: Dover Publications^⁠(d), pp. xiv+352, ISBN 978-0-486-66721-8 
• Kreyszig, Erwin (1999), Advanced Engineering Mathematics (ed. 8th), New York: Wiley, ISBN 0-471-15496-2 
• Luenberger, David (1997), Optimization by vector space methods, New York: Wiley, ISBN 978-0-471-18117-0 
• Mac Lane, Saunders (1998), Categories for the Working Mathematician^⁠(d) (ed. 2nd), Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-98403-2 
• Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation^⁠(d), W. H. Freeman, ISBN 978-0-7167-0344-0 
• Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications^⁠(d), ISBN 978-0-486-43235-9 
• Schönhage, A.; Strassen, Volker (1971), „Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)” (PDF), Computing (în germană), 7: 281–292, doi:10.1007/bf02242355, ISSN 0010-485X ^{[nefuncțională]}
• Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish 
• Stewart, Ian (1975), Galois Theory, Chapman and Hall^⁠(d) Mathematics Series, Londra: Chapman and Hall^⁠(d), ISBN 0-412-10800-3 
• Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Prentice Hall^⁠(d), ISBN 978-0-13-535732-3 
• Wallace, G.K. (1992), „The JPEG still picture compression standard”, IEEE Transactions on Consumer Electronics, 38 (1): xviii–xxxiv, doi:10.1109/30.125072, ISSN 0098-3063 
• Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259. 

Legături externe

• en Hazewinkel, Michiel, ed. (2001), „Vector space”, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• en O prelegere despre concepte fundamentale referitoare la spații vectoriale (ținută la MIT)
• en Simulator grafic pentru conceptele de generare, liniar-dependență, bază și dimensiune