Sferă unitate
În matematică o sferă unitate este o sferă cu raza 1 cu centrul dat. Mai general, este mulțimea punctelor (locul geometric al punctelor) aflate la distanța 1 de punctul fix din centru, de unde se pot folosi diferite norme ca generalizări ale „distanței”. O bilă unitate este mulțimea închisă a punctelor aflate la o distanță mai mică sau egală cu 1 de punctul fix din centru. Uzual centrul este originea spațiului, astfel că se poate vorbi despre „sfera unitate” sau „bila unitate” (unice). Cercul unitate și discul unitate sunt cazuri particulare.
Importanța sferei unitate este că orice sferă poate fi transformată într-o sferă unitate printr-o combinație de translație și scalare. În acest fel, proprietățile sferelor în general pot fi reduse la studiul sferei unitate.
Sfere și bile unitate în spațiul euclidian
[modificare | modificare sursă]În spațiul euclidian n-dimensional, sfera unitate n−1 dimensională este mulțimea tuturor punctelor care satisfac ecuația
Bila deschisă n-dimensională este mulțimea tuturor punctelor care satisfac inegalitatea
iar bila închisă n-dimensională este mulțimea tuturor punctelor care satisfac inegalitatea
Formule generale pentru suprafață și volum
[modificare | modificare sursă]Ecuația clasică a unei sfere unitate este cea a elipsoidului cu raza 1 și fără modificări ale axelor x, y sau z:
Volumul bilei unitate din spațiul euclidian n-dimensional și suprafața sferei unitate apar în multe formule importante din analiza matematică. Volumul bilei unitate n-dimensionale, notat Vn, poate fi exprimat utilizând funcția gamma:
unde n!! este dublul factorial(d).
Hipervolumul sferei unitate (n−1)-dimensionale (adică aria frontierei bilei unitate n-dimensionale), notată An, se poate exprima ca
unde ultima egalitate este valabilă doar pentru n > 0. De exemplu, este "aria" frontierei bilei unitate , care este formată din doar două puncte. Apoi este "aria" frontierei discului unitate, care este circumferința cercului unitate. este "aria" frontierei bilei unitate , care este aria suprafeței sferei unitate .
Suprafețele și volumele pentru unele valori ale lui sunt:
| (aria suprafeței) | (volumul) | |||
|---|---|---|---|---|
| 0 | 0 | 1 | ||
| 1 | 2 | 2 | ||
| 2 | 6.283 | 3.141 | ||
| 3 | 12.57 | 4.189 | ||
| 4 | 19.74 | 4.935 | ||
| 5 | 26.32 | 5.264 | ||
| 6 | 31.01 | 5.168 | ||
| 7 | 33.07 | 4.725 | ||
| 8 | 32.47 | 4.059 | ||
| 9 | 29.69 | 3.299 | ||
| 10 | 25.50 | 2.550 | ||
unde valorile zecimale pentru n ≥ 2 sunt rotunjite la precizia afișării.
Recursivitate
[modificare | modificare sursă]Valorile An satisfac relațiile recursive:
- pentru .
Valorile Vn satisfac relațiile recursive:
- pentru .
Dimensiuni fracționare
[modificare | modificare sursă]Formulele pentru An și Vn pot fi calculate pentru orice număr real n ≥ 0, și pot fi împrejurări când este necesar să se calculeze aria sferei sau volumul bilei pentru cazul că n nu este un întreg nenegativ.
Alte raze
[modificare | modificare sursă]Aria suprafeței unei sfere (n−1)-dimensionale cu raza r este An rn−1 iar volumul unei bile n-dimensionale cu raza r este Vn rn. De exemplu aria este A = 4π r 2 pentru suprafața bilei tridimensionale de rază r, iar volumul ei este V = 4π r 3 / 3.
Bile unitate în spații vectoriale normate
[modificare | modificare sursă]Mai exact, bila unitate deschisă într-un spațiu vectorial normat , cu norma , este
Este interiorul bilei unitate închise (V,||·||):
Aceasta din urmă este reuniunea disjunctă a noțiunii precedente și a frontierei lor comune, sfera unitate a (V,||·||):
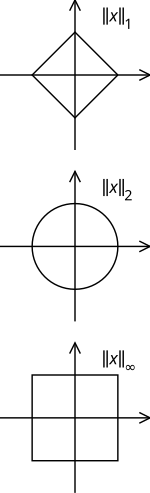
„Forma” bilei unitate depinde în totalitate de norma aleasă; poate avea „colțuri” și, de exemplu, în cazul normei maxime din Rn, poate arăta ca [−1,1]n. Cu norma obișnuite a spațiului Hilbert, bazată în cazul finit dimensional pe distanța euclidiană, se obține ca bilă unitate o „bilă rotundă”, naturală. Ceea ce se înțelege de obicei prin sfera unitate este frontiera sa.
Fie Se definește norma uzuală pentru p ≥ 1 drept:
Atunci este norma uzuală a spațiului Hilbert. este numită norma Hamming sau norma . Condiția p ≥ 1 este necesară în definiția normei , deoarece în orice spațiu normat bila unitate trebuie să fie convexă, ca o consecință a inegalității triunghiului. Notația pentru norma maximă (infinită) a lui x este .
De notat că pentru circumferințele ale bilelor unitate bidimensionale (n = 2), există:
- este valoarea minimă.
- este valoarea maximă.
Generalizări
[modificare | modificare sursă]Spații metrice
[modificare | modificare sursă]Toate cele trei definiții de mai sus pot fi generalizate direct la un spațiu metric, în raport cu o origine aleasă. Totuși, considerațiile topologice (interior, închidere, frontieră) nu trebuie să se aplice în același mod (de exemplu, în spațiile ultrametrice, toate cele trei sunt simultan mulțimi deschise și închise), iar sfera unitară poate fi chiar goală în unele spații metrice.
Forme pătratice
[modificare | modificare sursă]Dacă V este un spațiu liniar cu o formă pătratică reală F:V → R, atunci { p ∈ V : F(p) = 1 } poate fi numită sfera unitate[1][2] sau cvasisfera unitate a V. De exemplu, când este egală cu 1, forma pătratică produce hiperbola unitate, care joacă rolul cercului unitate în planul numerelor complexe hiperbolice(d). Similar, forma pătratică x2 produce o pereche de drepte pentru sfera unitate în planul numerelor duale(d).
Note
[modificare | modificare sursă]- ^ en Takashi Ono (1994) Variations on a Theme of Euler: quadratic forms, elliptic curves, and Hopf maps, chapter 5: Quadratic spherical maps, page 165, Plenum Press, ISBN: 0-306-44789-4
- ^ en F. Reese Harvey (1990) Spinors and calibrations, "Generalized Spheres", page 42, Academic Press, ISBN: 0-12-329650-1
Bibliografie
[modificare | modificare sursă]- en Mahlon M. Day (1958) Normed Linear Spaces, page 24, Springer-Verlag.
- en Deza, E.; Deza, M. (), Dictionary of Distances, Elsevier, ISBN 0-444-52087-2. Reviewed in Newsletter of the European Mathematical Society 64 (June 2007), p. 57. This book is organized as a list of distances of many types, each with a brief description.










![{\displaystyle [-1,1]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2016a25b4496666df761c56045fc221d3fbd2c08)






















































