Rotondă pentagonală

Rotondă pentagonală
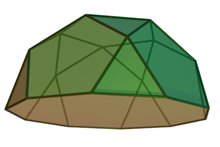(model 3D)
Descriere
Tip	poliedru Johnson J5 - J6 - J7
Fețe	17 (10 triunghiuri echilaterale         6 pentagoane regulate         1 decagon regulat)
Laturi (muchii)	35
Vârfuri	20
χ	2
Configurația vârfului	10 (3.5.3.5); 10 (3.5.10)
Grup de simetrie	C5v, [5], (*55), ordin 10
Arie	≈ 22,347 a2   (a = latura)
Volum	≈   6,918 a3   (a = latura)
Proprietăți	convexă
Desfășurată

În geometrie rotonda pentagonală este o rotondă la care fața opusă bazei este un pentagon regulat. Este poliedrul Johnson J₆. Poate fi văzută ca o jumătate dintr-un icosidodecaedru, sau ca jumătate dintr-o ortobirotondă pentagonală. Având 17 fețe, este un heptadecaedru.

Mărimi asociate

Următoarele formule pentru înălțime h, arie A, volum V și raza sferei circumscrise R sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

$h={\sqrt {1+{\frac {2}{\sqrt {5}}}}}\,a\approx 1,376382\,a\,,$

${\begin{aligned}A&={\frac {1}{2}}{\sqrt {5\left(145+58{\sqrt {5}}+2{\sqrt {30\left(65+29{\sqrt {5}}\right)}}\right)}}\,a^{2}\\&={\frac {5{\sqrt {3}}+{\sqrt {10\left(65+29{\sqrt {5}}\right)}}}{2}}\,a^{2}\approx 22,347200\,a^{2},\end{aligned}}$

$V={\frac {45+17{\sqrt {5}}}{12}}\,a^{3}\approx 6,917763\,a^{3},$

$R={\frac {1+{\sqrt {5}}}{2}}\,a\approx 1,618034\,a\,.$

Poliedru dual

Dualul rotundei pentagonale are 20 de fețe: 10 triunghiulare, 5 rombice și 5 romboidale.

Dualul rotondei pentagonale	Desfășurata dualului

Bibliografie

• en Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
• en Zalgaller, Victor (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN.  The first proof that there are only 92 Johnson solids.

Legături externe

• Materiale media legate de rotondă pentagonală la Wikimedia Commons
• en Eric W. Weisstein, Pentagonal rotunda la MathWorld.
• en Eric W. Weisstein, Johnson solid la MathWorld.