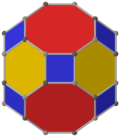
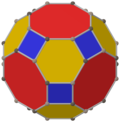
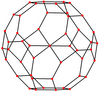
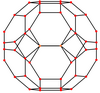
Cuboctaedru trunchiat
| Cuboctaedru trunchiat | |
 | |
| (animație și model 3D) | |
| Descriere | |
|---|---|
| Tip | Poliedru arhimedic (Poliedru uniform) |
| Fețe | 26 (12 pătrate, 8 hexagoane, 6 octogoane) |
| Laturi (muchii) | 72 |
| Vârfuri | 48 |
| χ | 2 |
| Configurația vârfului | 4.6.8 |
| Simbol Wythoff | 2 3 4 | |
| Simbol Schläfli | tr{4,3} sau t0,1,2{4,3} |
| Simbol Conway | bC sau taC |
| Diagramă Coxeter | |
| Grup de simetrie | Oh, B3, [4,3], (*432), ordin 48 |
| Grup de rotație | O, [4,3]+, (432), ordin 24 |
| Arie | ≈ 61,755 a2 (a = latura) |
| Volum | ≈ 41,799 a3 (a = latura) |
| Unghi diedru | 4-6: arccos(−√63) = 144° 44′ 08″ 4-8: arccos(−√23) = 135° 6-8: arccos(−√33) = 125°15′51″ |
| Poliedru dual | Dodecaedru disdiakis |
| Proprietăți | Poliedru semiregulat (zonoedru) convex cu fețe poligoane regulate, tranzitiv pe vârfuri |
| Figura vârfului | |
 | |
| Desfășurată | |
 | |
În geometrie cuboctaedrul trunchiat este un poliedru arhimedic. Are 26 de fețe regulate (12 pătrate, 8 fețe hexagonale și 6 octogonale), 72 de laturi și 48 de vârfuri. Deoarece fiecare dintre fețele sale are simetrie față de centru (echivalent, simetrie de rotație de 180°), cuboctaedrul trunchiat este un zonoedru. Împreună cu prisma octogonală, cuboctaedrul trunchiat poate tesela spațiul ca fagure cubic omnitrunchiat.
Are indicele de poliedru uniform U11,[1] indicele Coxeter C23 și indicele Wenninger W15.
Nume alternative[modificare | modificare sursă]
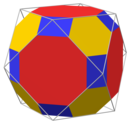
Numele de cuboctaedrul trunchiat i-a fost dat de Johannes Kepler. Aceste nume poate crea confuzii, deoarece actual prin trunchiere un cuboctaedru are dreptunghiuri în locul pătratelor, însă acel poliedru neuniform este topologic echivalent cu poliedrul arhimedic numit astfel (nu tocmai riguros). Alte nume sunt:
- Cuboctaedru rombitrunchiat (Magnus Wenninger[2]),
- Cub omnitrunchiat sau cub cantitrunchiat (Norman Johnson),
- Cub teșit (notația Conway a poliedrelor).
Există un poliedru uniform neconvex cu un nume asemănător: marele rombicuboctaedru neconvex.
Coordonate carteziene[modificare | modificare sursă]
Coordonatele carteziene ale vârfurilor unui cuboctaedru trunchiat având lungimea laturii 2 și centrat în origine sunt toate permutările:
- .
Arie și volum[modificare | modificare sursă]
Aria A și volumul V ale cuboctaedrului trunchiat cu lungimea laturii a sunt:
Divizare[modificare | modificare sursă]

|

|
Cuboctaedrul trunchiat este anvelopa convexă a unui rombicuboctaedru cu cuburi deasupra celor 12 pătrate cu axe de simetrie cu două poziții. Restul spațiului său poate fi divizat în 6 cupole pătrate sub octogoane și 8 cupole triunghiulare sub hexagoane.
Un cuboctaedru trunchiat divizat poate crea un toroid Stewart de genul 5, 7 sau 11 prin îndepărtarea rombicuboctaedrului central și fie a celor 6 cupole pătrate, fie a celor 8 cupole triunghiulare sau, respectiv, a celor 12 cuburi. De asemenea, mulți alți toroizi cu simetrie inferioară pot fi construiți prin îndepărtarea rombicuboctaedrului central și a unui subset al celorlalte componente de divizare. De exemplu, îndepărtarea a 4 dintre cupolele triunghiulare creează un toroid de genul 3; dacă aceste cupole sunt alese corespunzător, atunci acest toroid are simetrie tetraedrică.[3][4]
| Toroizi Stewart | |||
|---|---|---|---|
| Genul 3 | Genul 5 | Genul 7 | Genul 11 |

|

|

|

|
Colorare ca poliedru uniform[modificare | modificare sursă]
Colorarea ca poliedru uniform se face cu câte o culoare pentru fiecare tip de față.
Proiecții ortogonale[modificare | modificare sursă]
Cuboctaedrul trunchiat are două proiecții ortogonale speciale în planele Coxeter A2 și B2 cu simetriile proiecțiilor [6] și [8], iar numeroase simetrii [2] pot fi construite în diferite plane de proiecție în raport cu elementele poliedrului.
Pavări sferice[modificare | modificare sursă]
Cuboctaedrul trunchiat poate fi reprezentat și ca o pavare sferică și proiectat pe plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu și ariile sau lungimile. Liniile drepte pe sferă sunt proiectate pe plan ca arce de cerc.

|

|

|

|
| Proiecție ortogonală | centrată pe pătrat | centrată pe hexagon | centrată pe octogon |
|---|---|---|---|
| Proiecții stereografice | |||
Grupul octaedric complet[modificare | modificare sursă]

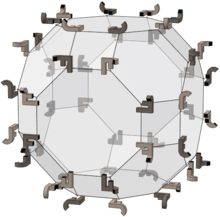
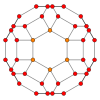
La fel ca multe alte poliedre, octaedrul trunchiat are o simetrie octaedrică completă, dar relația sa cu grupul octaedric complet este mai complexă decât aceasta: cele 48 de vârfuri corespund elementelor grupului și fiecare față a dualului său este un domeniu fundamental al grupului.
Imaginea din dreapta arată cele 48 de permutări din grup aplicate unui obiect. Cele 24 de elemente „F” de culoare deschisă sunt rotații, iar cele de culoare închisă sunt reflexiile lor.
Laturile poliedrului corespund celor 9 reflexii din grup:
- Cele dintre octogoane și pătrate corespund celor 3 reflexii dintre octogoanele opuse.
- Laturile hexagonale corespund celor 6 reflexii dintre pătratele opuse.
- (Nu există reflexii între hexagoanele opuse.)
Subgrupurile corespund poliedrelor care au în comun vârfurile respective cu cele ale octaedrului trunchiat.
De exemplu, cele 3 subgrupuri cu 24 de elemente corespund unui cub snub neuniform cu simetrie octaedrică chirală, unui rombicuboctaedru neuniform cu simetrie piritoedrică (octaedrul snub cantic) și unui octaedru trunchiat neuniform cu simetrie tetraedrică completă. Subgrupul unic cu 12 elemente este grupul altern A4. Acesta corespunde unui icosaedru neuniform cu simetrie tetraedrică chirală.
| Subgrupuri și poliedrele corespondente | ||||
|---|---|---|---|---|
| Cuboctaedru trunchiat tr{4,3} |
Cub snub sr{4,3} |
Rombicuboctaedru s2{3,4} |
Octaedru trunchiat h1,2{4,3} |
Icosaedru |
| [4,3] Octaedrică completă |
[4,3]+ Octaedrică chirală |
[4,3+] Simetrie piritoedrică |
[1+,4,3] = [3,3] Tetraedrică completă |
[1+,4,3+] = [3,3]+ Tetraedrică chirală |

|

|

|

|

|
| toate 48 vârfuri | 24 vârfuri | 12 vârfuri | ||
Poliedre înrudite[modificare | modificare sursă]

|

|
| Tetraedrul și cubul „papion” conțin două fețe trapezoidale în locul fiecărui pătrat.[5] | |
Cuboctaedrul trunchiat face parte dintr-o familie de poliedre uniforme înrudite cu cubul și octaedrul regulat.
| Poliedre octaedrice uniforme | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetrie: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||

|

|
 
|
 
|
 
|
 
|

|

|
 
| ||
| Dualele celor de mai sus | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |

|

|

|

|

|

|

|

|

|

|

|
Acest poliedru face parte dintr-o secvență de modele uniforme cu configurația vârfului (4.6.2p) și diagrama Coxeter–Dynkin ![]()
![]()
![]()
![]()
![]() . Pentru p < 6, membrii secvenței sunt poliedre omnitrunchiate (zonoedre), prezentate mai jos ca pavări sferice. Pentru p < 6, acestea sunt pavări ale planului hiperbolic, începând cu pavare triheptagonală trunchiată.
. Pentru p < 6, membrii secvenței sunt poliedre omnitrunchiate (zonoedre), prezentate mai jos ca pavări sferice. Pentru p < 6, acestea sunt pavări ale planului hiperbolic, începând cu pavare triheptagonală trunchiată.
| Variante de pavări omnitrunchiate cu simetrie *n32: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetrie *n32 [n,3] |
Sferice | Euclid. | Hiperb. compacte | Paraco. | Hiperbolice necompacte | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Imagini | 
|

|

|

|

|

|

|

|

|

|

| |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duale | 
|

|

|

|

|

|

|

|

|

|

|

|
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| Variante de pavări omnitrunchiate cu simetrie *n42: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simetrie *n42 [n,3] |
Sferice | Euclidiană | Hiperbolice compacte | Paracomp. | ||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Figuri omnitrunchiate |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Duale omnitrunchiate |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
Este primul dintr-o serie de hipercuburi cantitrunchiate.
 
|
 
|
 
|
 
|
 
|
 
|
| Cuboctaedru trunchiat | Tesseract cantitrunchiat | 5-cub cantitrunchiat | 6-cub cantitrunchiat | 7-cub cantitrunchiat | 8-cub cantitrunchiat |
Note[modificare | modificare sursă]
- ^ en Eric W. Weisstein, Uniform Polyhedron la MathWorld.
- ^ en Wenninger, Magnus (), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, MR 0467493 (Model 15, p. 29)
- ^ en B. M. Stewart (1970), Adventures Among the Toroids, ISBN: 978-0-686-11936-4
- ^ en Doskey, Alex. „Adventures Among the Toroids - Chapter 5 - Simplest (R)(A)(Q)(T) Toroids of genus p=1”. www.doskey.com.
- ^ en Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons Arhivat în , la Wayback Machine. Craig S. Kaplan
Bibliografie[modificare | modificare sursă]
- en Cromwell, P. (). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
 Materiale media legate de cuboctaedru trunchiat la Wikimedia Commons
Materiale media legate de cuboctaedru trunchiat la Wikimedia Commons- en Eric W. Weisstein, Great rhombicuboctahedron la MathWorld.
- en Eric W. Weisstein, Archimedean solid la MathWorld.
- en Eric W. Weisstein, Great rhombicuboctahedral graph la MathWorld.
- en Editable printable net of a truncated cuboctahedron with interactive 3D view
- en The Uniform Polyhedra
- en Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- en Great rhombicuboctahedron: paper strips for plaiting Arhivat în , la Wayback Machine.
- en Klitzing, Richard. „3D uniform polyhedra”. Cheie: girco