Înălțime (geometrie)

Înălţimile unui triunghi sunt concurente (în ortocentru)

Înălțimea într-un triunghi reprezintă segmentul determinat de un vârf al triunghiului și piciorul perpendicularei din acel vârf pe dreapta ce conține latura opusă vârfului.

Proprietăți ale înălțimilor poligonale

Concurența înălțimilor unui triunghi

Cele trei înălțimi ale unui triunghi sunt concurente. Punctul lor de intersecție, H, se numește ortocentru. Triunghiul având ca vârfuri picioarele înălțimilor se numește triunghi ortic.

Demonstrație. Fie triunghiul ABC și A”, B”, C” - picioarele perpendicularelor vârfurilor pe laturile opuse.

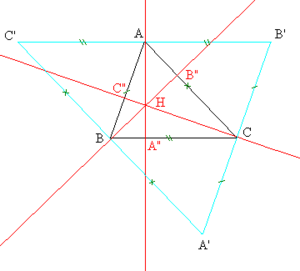
Prin vârfurile triunghiului ABC ducem paralele la laturile opuse, care se intersectează în punctele A', B', C' ca în figura alăturată. Din construcție, ABCB' și BCAC' sunt paralelograme, deci $|BC|=|AC'|=|AB'|$. Pentru că $BC||B'C'$ și $AA''\perp BC$, rezultă că $AA''\perp B'C'$. Deci AA' este mediatoarea segmentului B'C'. Analog, BB” și CC” sunt mediatoarele segmentelor A'C' respectiv A'B'. Prin urmare, conform concurenței mediatoarelor unui triunghi, rezultă că și înălțimile triunghiului ABC sunt concurente.

Punct interior unui triunghi

Dacă p₁, p₂ și p₃ sunt distanțele de la orice punct interior P la laturi și h₁, h₂, and h₃ înălțimile pe respectivele laturi, atunci este valabilă egalitatea:

${\frac {p_{1}}{h_{1}}}+{\frac {p_{2}}{h_{2}}}+{\frac {p_{3}}{h_{3}}}=1.$

Poligoane

În poligoane înălțimea poate ajuta la determinarea ariei acestui poligon:

• la triunghi: $S={\frac {h*a}{2}}$, a este latura pe care cade înălțimea;
• la triunghiul dreptunghic: catetele sunt înălțimi, deci $S={\frac {c1*c2}{2}}$ sau $S={\frac {h*ip}{2}}$;

• într-un triunghi dreptunghic, este egală cu produsul proiecțiilor sale pe ipotenuza sau cu produsul catetelor împărțit la ipotenuză;

• la trapez: $S={\frac {h*(b+B)}{2}}$, b și B fiind cele două baze ale trapezului;
• la paralelogram: $S=h*l$, l este latura pe care cade înălțimea.

Înălțimea unei piramide este segmentul coborât din vârf perpendicular pe planul bazei

Vezi și

• Bisectoare
• Mediatoare
• Mediană
• Linie mijlocie
• Triunghi
• Triunghi ortic