Tetraedru trunchiat

Descriere
Tetraedru trunchiat

(animație și model 3D)
Tip	Poliedru arhimedic (poliedru uniform)
Fețe	8 (4 triunghiuri, 4 hexagoane)
Laturi (muchii)	18
Vârfuri	12
χ	2
Configurația vârfului	3.6.6
Simbol Wythoff	2 3 \| 3
Simbol Schläfli	t{3,3} = h₂{4,3} t_0,1{3,3}
Simbol Conway	tT
Diagramă Coxeter	=
Grup de simetrie	T_d, A₃, [3,3], (*332), ordin 24
Grup de rotație	T, [3,3]⁺, (332), ordin 12
Arie	≈ 12,124 a² (a = latura)
Volum	≈ 2,710 a³ (a = latura)
Unghi diedru	3-6: 109° 28′ 16″ 6-6: 70° 31′ 44″
Poliedru dual	Tetraedru triakis
Proprietăți	Poliedru semiregulat, convex cu fețe poligoane regulate, tranzitiv pe vârfuri
Figura vârfului

Desfășurată

În geometrie tetraedrul trunchiat este un poliedru arhimedic. Are 4 fețe hexagoane regulate, 4 fețe triunghiuri echilaterale, 12 vârfuri și 18 laturi (de două tipuri). Poate fi construit prin trunchierea tuturor celor 4 vârfuri ale unui tetraedru regulat la o treime din lungimea laturii inițiale.

O trunchiere mai intensă, care elimină din fiecare vârf câte un tetraedru cu latura jumătate din lungimea laturii inițiale, se numește rectificare și transformă tetraedrul într-un octaedru.^[1]

Tetraedrul trunchiat poate fi considerat un cub cantic, cu diagrama Coxeter, , aând jumătate din vârfurile unui cub cantelat (rombicuboctaedru), . Există două poziții duale ale acestei construcții, iar combinarea lor creează compusul uniform de două tetraedre trunchiate.

Are indicele de poliedru uniform U₀₂,^[2] indicele Coxeter C₁₆ și indicele Wenninger W₆.

Mărimi asociate[modificare | modificare sursă]

Coordonate carteziene[modificare | modificare sursă]

Coordonatele carteziene ale celor 12 vârfuri ale tetraedrului trunchiat centrat în origine, cu lungimea laturii √8 sunt permutările lui (±1,±1,±3) cu un număr par de semne minus:

(+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
(−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
(−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
(+3,−1,−1), (+1,−3,−1), (+1,−1,−3)

Arie și volum[modificare | modificare sursă]

Aria A și volumul V ale unui tetraedru trunchiat cu lungimea laturii a sunt:

A=7{\sqrt {3}}\,a^{2}\approx 12,1243556~a^{2},

V={\frac {23}{12}}{\sqrt {2}}\,a^{3}\approx 2,710576~a^{3}.

Proiecții[modificare | modificare sursă]


Proiecție ortogonală în coordonate carteziene în cubul de încadrare (±3,±3,±3).	Fețele hexagonale ale tetraedrelor trunchiate pot fi împărțite în 6 triunghiuri echilaterale coplanare. Cele 4 noi vârfuri au coordonatele carteziene: (−1,−1,−1), (−1,+1,+1), (+1,−1,+1), (+1,+1,−1). Astfel poate fi descompus în 4 octaedre (roșii) și 6 tetraedre (galbene).	Setul de permutări ale vârfurilor (±1,±1,±3) cu un număr impar de semne minus formează un tetraedru trunchiat complementar, care combinat cu cel inițial formează un compus uniform.

Proiecții ortogonale
Centrat pe	Normala laturii	Normala feței	Latură	Față
Proiecție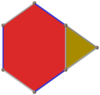
Cadru de sârmă
Dual
Simetrie proiectivă	[1]	[1]	[4]	[3]

Pavare sferică[modificare | modificare sursă]

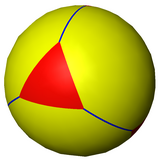
Tetraedrul trunchiat poate fi reprezentat și ca o pavare sferică și proiectat în plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu și ariile sau lungimile. Liniile „drepte” pe sferă sunt proiectate în plan ca arce de cerc.

Proiecție ortogonală	Proiecții stereografice
	centrat pe triunghiuri	centrat pe hexagoane

Poliedre înrudite[modificare | modificare sursă]

Familia poliedrelor tetraedrice uniforme
Simetrie: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duale ale poliedrelor uniforme

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Este, de asemenea, o parte dintr-un set de poliedre cantice și pavări cu configurația vârfului 3.6.n.6. În această construcție Wythoff, laturile dintre hexagoane reprezintă digoane degenerate.

Simetrii orbifold n33 ale pavărilor cantice: 3.6.n.6*
	Orbifold *n32	Sferică	Euclidiană	Hiperbolice compacte			Paracompactă
	Orbifold *n32	*332	*333	*433	*533	*633...	*∞33
Figură cantică
Configurația vârfului		3.6.2.6	3.6.3.6	3.6.4.6	3.6.5.6	3.6.6.6	3.6.∞.6

Variante de simetrie[modificare | modificare sursă]

Acest poliedru este înrudit topologic de familia de poliedre trunchiate uniforme cu simetriile din grupul Coxeter ale configurațiilor vârfurilor (3.2n.2n) și [n,3].

Variante de simetrii *n32 ale pavărilor sferice trunchiate: t{n,3}
Simetrii *n32 [n,3]	Sferice				Euclidiană	Hiperb. compacte		Paracomp.
Simetrii *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figuri trunchiate
Schläfli	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}
Figuri triakis
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

Note[modificare | modificare sursă]

^ en Chisholm, Matt; Avnet, Jeremy (1997). „Truncated Trickery: Truncatering”. theory.org. Accesat în 2 septembrie 2013.
^ en Eric W. Weisstein, Uniform Polyhedron la MathWorld.

Bibliografie[modificare | modificare sursă]

en Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., ISBN: 0-486-23729-X. (Section 3-9)
en Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press