Cuboid
În geometrie, un cuboid este un hexaedru, adică un poliedru cu șase fețe. Fețele sale sunt patrulatere. „Cuboid” înseamnă „de formă aproximativ cubică”[1], în sensul că, prin schimbarea lungimii laturilor sau/și a unghiurilor dintre laturi și fețe, un cuboid se poate transforma într-un cub. În limbajul matematic, un cuboid este un poliedru convex al cărui graf poliedric este același cu cel al unui cub.
Cazurile particulare: cubul, cu 6 pătrate drept fețe; prisma dreptunghiulară; paralelipipedul dreptunghic, cu 6 dreptunghiuri drept fețe. Atât la cub, cât și la paralelipipedul dreptunghic, fețele adiacente se întâlnesc într-un unghi drept.[2][3]
Cuboizi oarecare[modificare | modificare sursă]
Caracteristica Euler a oricărui poliedru convex leagă numerele de fețe F, de vârfuri V și de laturi E ale oricărui poliedru convex prin formula
Deoarece la fel cu un cub, un cuboid are 6 fețe, 8 vârfuri și 12 laturi, aceasta dă 6 − 12 + 8 = 2. Alături de prismele patrulatere, orice paralelipiped este un cuboid de acest tip, chiar și un trunchi de patrulater (formă obținută prin trunchierea vârfului unei piramide patrulatere).
| Imagine | 
|

|
|

|

|

|

|
|---|---|---|---|---|---|---|---|
| Denumire (fețe) |
Cub (Pătrat) |
Paralelipiped dreptunghic (trei perechi de dreptunghiuri) |
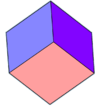
Trapezoedru trigonal (romburi congruente) |
Trapezoedru trigonal (patrulatere congruente) |
Trunchi patrulater (piramidă patrulateră trunchiată la apex) |
Paralelipiped (trei perechi de paralelograme) |
Romboedru (trei perechi de romburi) |
| Simetrie | Oh, [4,3], (*432) ordin 48 |
D2h, [2,2], (*222) ordin 8 |
D3d, [2+,6], (2*3) ordin 12 |
D3, [2,3]+, (223) ordin 6 |
C4v, [4], (*44) ordin 8 |
Ci, [2+,2+], (×) ordin 2 | |
Paralelipiped dreptunghic[modificare | modificare sursă]
Într-un paralelipiped dreptunghic, toate unghiurile sunt drepte, iar fețele opuse sunt egale. Termenul de paralelipiped ortogonal este și el folosit pentru a desemna acest poliedru. Prin definiție, aceasta îl face o prismă dreptunghiulară, însă termenii prismă dreptunghiulară și prismă alungită sunt ambigui, deoarece nu specifică toate unghiurile.
Note[modificare | modificare sursă]
- ^ „cuboid” la DEX online
- ^ en Robertson, Stewart Alexander (). Polytopes and Symmetry
 . Cambridge University Press. p. 75. ISBN 9780521277396.
. Cambridge University Press. p. 75. ISBN 9780521277396.
- ^ en Dupuis, Nathan Fellowes (). Elements of Synthetic Solid Geometry. Macmillan. p. 53. Accesat în .
Bibliografie[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
 Materiale media legate de cuboid la Wikimedia Commons
Materiale media legate de cuboid la Wikimedia Commons Materiale media legate de cuboid la Wikimedia Commons
Materiale media legate de cuboid la Wikimedia Commons- en Rectangular prism and cuboid Paper models and pictures

