Octaedru trunchiat

Descriere
Octaedru trunchiat

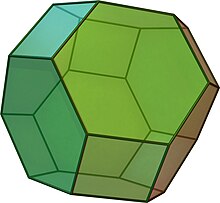(animație și model 3D)
Tip	Poliedru arhimedic (Poliedru uniform)
Fețe	14 (6 pătrate, 8 hexagoane)
Laturi (muchii)	36
Vârfuri	24
χ	2
Configurația vârfului	4.6.6
Simbol Wythoff	2 4 \| 3 3 3 2 \|
Simbol Schläfli	t{3,4} tr{3,3} sau $t{\begin{Bmatrix}3\\3\end{Bmatrix}}$
Simbol Conway	tO sau bT
Diagramă Coxeter
Grup de simetrie	O_h, B₃, [4,3], (432), ordin 48 T_h, [3,3] and (332), ordin 24
Grup de rotație	O, [4,3]⁺, (432), ordin 24
Arie	≈ 26,785 a² (a = latura)
Volum	≈ 11,314 a³ (a = latura)
Unghi diedru	4-6: arccos(−1/√3) = 125° 15′ 51″ 6-6: arccos(−1/3) = 109° 28′ 16″
Poliedru dual	Hexaedru tetrakis
Proprietăți	Poliedru semiregulat (paraleloedru, permutoedru, zonoedru) convex cu fețe poligoane regulate, tranzitiv pe vârfuri
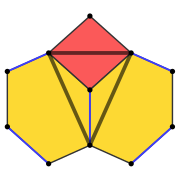
Figura vârfului

Desfășurată

Dual: Hexaedru tetrakis

În geometrie octaedrul trunchiat este un poliedru arhimedic. Se obține dintr-un octaedru regulat prin îndepărtarea a șase piramide, câte una la fiecare vârf al octaedrului. Are 14 fețe regulate (6 pătrat și 8 fețe hexagonale), 36 de laturi și 24 de vârfuri. Deoarece fiecare dintre fețele sale are simetrie față de centru, octaedrul trunchiat este un zonoedru. La fel cu cubul, poate tesela spațiul tridimensional, ca un permutoedru.

Poliedrul său dual este hexaedrul tetrakis. Dacă octaedrul trunchiat inițial are lungimea laturii 1, dualul său are lungimile laturilor 9/8√2 și 3/2√2.

Are indicele de poliedru uniform U₀₈,^[1] indicele Coxeter C₂₀ și indicele Wenninger W₇.

Construcție, arie și volum[modificare | modificare sursă]

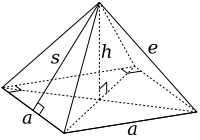
Un octaedru trunchiat este construit dintr-un octaedru regulat cu lungimea laturii 3a prin îndepărtarea a șase piramide pătrate drepte, câte una din fiecare vârf. Aceste piramide au atât lungimea laturii de bază (a) cât și lungimea laturii laterale (e) egală cu a, pentru a forma triunghiuri echilaterale. Aria bazei acestora este a². De observat că această formă este asemenea cu o jumătate de octaedru sau cu poliedrul Johnson J1.

Din proprietățile piramidelor pătrate se obțin apotema s și înălțimea h ale unei piramide îndepărtate:

{\begin{aligned}h&={\sqrt {e^{2}-{\tfrac {1}{2}}a^{2}}}&&={\tfrac {1}{\sqrt {2}}}a\\s&={\sqrt {h^{2}+{\tfrac {1}{4}}a^{2}}}&&={\sqrt {{\tfrac {1}{2}}a^{2}+{\tfrac {1}{4}}a^{2}}}&&={\tfrac {\sqrt {3}}{2}}a\end{aligned}}

Volumul V₁ al piramidei îndepărtate este

V_{1}={\tfrac {1}{3}}a^{2}h={\tfrac {\sqrt {2}}{6}}a^{3}

Deoarece șase piramide sunt îndepărtate prin trunchiere, volumul octaedrului trunchiat este mai mic decât al octaedrului inițial cu √2a³.

Aria A și volumul V ale octaedrului trunchiat cu latura de lungime a sunt:

{\begin{aligned}A&=\left(6+12{\sqrt {3}}\right)a^{2}&&\approx 26,784\,6097\,a^{2}\\V&=8{\sqrt {2}}a^{3}&&\approx 11,313\,7085\,a^{3}.\end{aligned}}

Proiecții ortogonale[modificare | modificare sursă]

Octaedrul trunchiat are cinci proiecții ortogonale speciale, centrate pe un vârf, pe două tipuri de muchii și două tipuri de fețe: hexagon și pătrat. Ultimele două corespund planelor Coxeter B₂ și A₂.

Proiecții ortogonale
Centrată pe	Vârf	Latură 4-6	Latură 6-6	Față pătrată	Față hexagonală
Poliedru
Cadru de sârmă
Dual
Simetrie proiectivă	[2]	[2]	[2]	[4]	[6]

Pavare sferică[modificare | modificare sursă]

Proiecție ortogonală	Proiecții stereografice
	centrată pe pătrat	centrată pe hexagon

Octaedrul trunchiat poate fi reprezentat și ca o pavare sferică și proiectat în plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu ariile sau lungimile. Liniile drepte pe sferă sunt proiectate în plan ca arce de cerc.

Coordonate[modificare | modificare sursă]


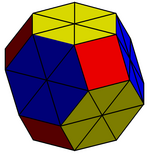
Proiecție ortogonală în cadrul (±2, ±2, ±2)	Octaedru trunchiat cu hexagoanele divizate în 6 triunghiuri coplanare. Există 8 noduri noi la (±1, ±1, ±1).	Octaedru trunchiat subdivizat topologic în triacontaedru rombic

Toate permutările lui (0, ±1, ±2) sunt coordonatele carteziene ale vârfurilor unui octaedru trunchiat cu lungimea laturii $a={\sqrt {2}}$ centrat în origine. Vârfurile sunt astfel și colțurile a 12 dreptunghiuri ale căror laturi lungi sunt paralele cu axele de coordonate.

Vectorii laturilor au coordonatele carteziene (0, ±1, ±1) și permutări ale acestora. Normalele fețelor (produsele vectoriale normalizate ale laturilor care au un vârf comun) ale celor 6 fețe pătrate sunt (0, 0, ±1), (0, ±1, 0) și (±1, 0, 0). Normalele celor 8 fețe hexagonale sunt (±1/√3, ±1/√3, ±1/√3). Produsul scalar al normalelor unei perechi de fețe este cosinusul unghiului diedru dintre fețele adiacente, fie −1/3, fie −1/√3. Unghiul diedru este aproximativ 1,910633 radiani (109,471°^[2]) între fețele hexagonale și 2,186276 radiani (125,263°^[3]) între o față hexagonală și una pătrată.

Divizare[modificare | modificare sursă]

Gen 2	Gen 3
D_3d, [2⁺,6], (2*3), ordin 12	T_d, [3,3], (*332), ordin 24

Octaedrul trunchiat poate fi divizat într-un octaedru central, înconjurat de 8 cupole triunghiulare pe fiecare față și 6 piramide pătrate deasupra vârfurilor.^[4]

Înlăturând octaedrul central și 2 sau 4 cupole triunghiulare creează doi toroizi Stewart, cu simetrie diedrală și tetraedrică:

Permutoedru[modificare | modificare sursă]

Octaedrul trunchiat poate fi reprezentat și prin coordonate și mai simetrice în patru dimensiuni: toate permutările lui (1, 2, 3, 4) formează vârfurile unui octaedru trunchiat în subspațiul tridimensional x + y + z + w = 10. Prin urmare, octaedrul trunchiat este permutoedrul de ordinul 4: fiecare vârf corespunde unei permutări a lui (1, 2, 3, 4) și fiecare latură reprezintă o singură interschimbare a două elemente dintr-o pereche.

Colorare ca poliedru uniform[modificare | modificare sursă]

Există două colorări uniforme, cu simetrie tetraedrică și simetrie octaedrică, și două colorări uniforme cu simetrie diedrală ca antiprismă triunghiulară trunchiată. Notația Conway a poliedrelor este dată în paranteze.

uniformă 1		uniformă 2
O_h, [4,3], (*432) ordin 48	T_d, [3,3], (*332) ordin 24	D_4h, [4,2], (*422) ordin 16	D_3d, [2⁺,6], (2*3) ordin 12
colorare 122	colorare 123	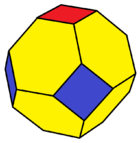colorare 122 și 322	colorare 122 și 123
Octaedru trunchiat (tO)	Tetraedru teșit (bT)	Bipiramidă pătrată trunchiată (tdP4)	Antiprismă triunghiulară trunchiată (tA3)

Poliedre înrudite[modificare | modificare sursă]

Octaedrul trunchiat face parte dintr-o familie de poliedre uniforme înrudite cu cubul și octaedrul regulat.

Poliedre octaedrice uniforme v • d • m
Simetrie: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= sau	= sau	=

Dualele celor de mai sus
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

De asemenea, există și ca omnitrunchiat în familia tetraedrelor:

Variante de pavări omnitrunchiate cu simetrie n32: 4.6.2n*
Simetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paraco.	Hiperbolice necompacte
Simetrie *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Imagini
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duale
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Familia poliedrelor tetraedrice uniforme
Simetrie: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duale ale poliedrelor uniforme

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Variante de simetrie[modificare | modificare sursă]

Acest poliedru face parte dintr-o secvență de modele uniforme cu configurația vârfului (4.6.2p) și diagrama Coxeter–Dynkin . Pentru p < 6, membrii secvenței sunt poliedre omnitrunchiate (zonoedre), prezentate mai jos ca pavări sferice. Pentru p > 6, acestea sunt pavări ale planului hiperbolic, începând cu pavare triheptagonală trunchiată.

Variante de simetrii *nn2 ale pavărilor omnitrunchiate: 4.2n.2n
Simetrie *nn2 [n,n]	Sferică		Euclidiană	Hiperbolică compactă				Paracomp.
Simetrie *nn2 [n,n]	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Imagine
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Dual
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Octaedrul trunchiat este înrudit din punct de vedere topologic ca parte a secvenței de poliedre și pavări uniforme cu figurile vârfului n.6.6, extinzându-se în planul hiperbolic:

Variante de simetrii *n32 ale pavărilor trunchiate: n.6.6
Sim. *n42 [n,3]	Sferică				Euclid.	Compactă		Paracomp.	Hiperbolică necompactă
Sim. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Figuri trunchiate
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
Figuri n-kis
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Octaedrul trunchiat este înrudit din punct de vedere topologic ca parte a secvenței de poliedre și pavări uniforme cu figurile vârfurilor 4,2n.2n, extinzându-se în planul hiperbolic:

Variante de simetrii *n42 ale pavărilor trunchiate: 4.2n.2n
Simetrie *n42 [n,4]	Sferică		Euclid.	Hiperbolică compactă				Paracomp.
Simetrie *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Figuri trunchiate
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Figuri n-kis
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Politopuri înrudite[modificare | modificare sursă]

Octaedrul trunchiat (cubul bitrunchiat), este primul dintr-o succesiune de hipercuburi trunchiate:

Hipercuburi bitrunchiate
Imagine							...
Nume	Cub bitrunchiat	Tesseract bitrunchiat	5-cub bitrunchiat	6-cub bitrunchiat	7-cub bitrunchiat	8-cub bitrunchiat
Coxeter
Figura vârfului	( )v{ }	{ }v{ }	{ }v{3}	{ }v{3,3}	{ }v{3,3,3}	{ }v{3,3,3,3}

Este posibil să se secționeze un tesseract cu un hiperplan, astfel încât secțiunea transversală a acestuia să fie un octaedru trunchiat.^[5]

Teselări[modificare | modificare sursă]

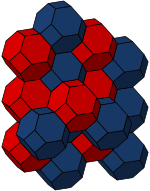
Octaedrul trunchiat există în trei faguri uniformi convecși:

Cubic bitrunchiat	Cubic cantitrunchiat	Cubic alternat trunchiat

Fagurele cubic bitrunchiat tranzitiv pe celule poate fi considerat o teselare Voronoi^⁠(d) a rețelei cubice centrate intern. Octaedrul trunchiat este unul dintre cele cinci paraleloedre.

Note[modificare | modificare sursă]

^ en Eric W. Weisstein, Uniform Polyhedron la MathWorld.
^ Șirul A156546 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
^ Șirul A195698 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
^ en Doskey, Alex. „Adventures Among the Toroids – Chapter 5 – Simplest (R)(A)(Q)(T) Toroids of genus p=1”. www.doskey.com.
^ en Borovik, Alexandre V.; Borovik, Anna (2010), „Exercise 14.4”, Mirrors and Reflections, Universitext, New York: Springer, p. 109, doi:10.1007/978-0-387-79066-4, ISBN 978-0-387-79065-7, MR 2561378

Bibliografie[modificare | modificare sursă]

en Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., ISBN: 0-486-23729-X. (Section 3-9)
en Freitas, Robert A. Jr. „Uniform space-filling using only truncated octahedra”. Figure 5.5 of Nanomedicine, Volume I: Basic Capabilities, Landes Bioscience, Georgetown, TX, 1999. Accesat în 8 septembrie 2006. Legătură externa în |publisher= (ajutor)
en Gaiha, P.; Guha, S.K. (1977). „Adjacent vertices on a permutohedron”. SIAM Journal on Applied Mathematics. 32 (2): 323–327. doi:10.1137/0132025.
en Hart, George W. „VRML model of truncated octahedron”. Virtual Polyhedra: The Encyclopedia of Polyhedra. Accesat în 8 septembrie 2006. Legătură externa în |publisher= (ajutor)
en Mäder, Roman. „The Uniform Polyhedra: Truncated Octahedron”. Accesat în 8 septembrie 2006.
en Alexandrov, A.D. (1958). Konvexe Polyeder. Berlin: Springer. p. 539. ISBN 3-540-23158-7.
en Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.

Legături externe[modificare | modificare sursă]

Materiale media legate de octaedru trunchiat la Wikimedia Commons
en Eric W. Weisstein, Truncated octahedron la MathWorld.
en Eric W. Weisstein, Octaedru trunchiat la MathWorld.
en Eric W. Weisstein, Truncated octahedral graph la MathWorld.
en Eric W. Weisstein, Permutohedron la MathWorld.
en Klitzing, Richard. „3D convex uniform polyhedra x3x4o - toe”.
en Editable printable net of a truncated octahedron with interactive 3D view

Portal Matematică

[1] Eric W. Weisstein, Uniform Polyhedron la MathWorld.

[2] Șirul A156546 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)

[3] Șirul A195698 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)

[4] Doskey, Alex. „Adventures Among the Toroids – Chapter 5 – Simplest (R)(A)(Q)(T) Toroids of genus p=1”. www.doskey.com.

[5] Borovik, Alexandre V.; Borovik, Anna (2010), „Exercise 14.4”, Mirrors and Reflections, Universitext, New York: Springer, p. 109, doi:10.1007/978-0-387-79066-4, ISBN 978-0-387-79065-7, MR 2561378

[1]

[2]

[3]

[4]

[5]