Icosaedru trunchiat
| Icosaedru trunchiat | |
 | |
| (animație și model 3D) | |
| Descriere | |
|---|---|
| Tip | Poliedru arhimedic (Poliedru uniform) |
| Fețe | 32 (12 pentagoane, 20 hexagoane) |
| Laturi (muchii) | 90 |
| Vârfuri | 60 |
| χ | 2 |
| Configurația vârfului | 5.6.6 |
| Simbol Wythoff | 2 5 | 3 |
| Simbol Schläfli | t{3,5} t0,1{3,5} |
| Simbol Conway | tI |
| Diagramă Coxeter | |
| Grup de simetrie | Ih, H3, [5,3], (*532), ordin 120 |
| Grup de rotație | I, [5,3]+, (532), ordin 60 |
| Arie | ≈ 72,607 a2 (a = latura) |
| Volum | ≈ 55,288 a3 (a = latura) |
| Unghi diedru | 6-6: 138,190° 6-5: 142,620° |
| Poliedru dual | Dodecaedru pentakis |
| Proprietăți | Poliedru semiregulat (permutoedru, zonoedru) convex cu fețe poligoane regulate, tranzitiv pe vârfuri |
| Figura vârfului | |
 | |
| Desfășurată | |
 | |
În geometrie icosaedrul trunchiat este un poliedru arhimedic cu 32 de fețe regulate (12 pentagoane și 20 de hexagoane), 90 de laturi și 60 de vârfuri. Dacă nu se specifică altfel, toate laturile sale au aceeași lungime. Este singurul poliedru uniform cu fețe care nu sunt triunghiuri sau pătrate. Deoarece fiecare dintre fețele sale are simetrie față de centru, icosaedrul trunchiat este un zonoedru.
Poliedrul său dual este dodecaedrul pentakis.
Are indicele de poliedru uniform U25,[1] indicele Coxeter C27 și indicele Wenninger W9. Este poliedrul Goldberg GPV(1,1) sau {5+,3}1,1.
Poate tesela spațiul hiperbolic sub forma fagurelui dodecaedric bitrunchiat de ordinul 5
Geometria sa este folosită la mingile de fotbal, realizate de obicei cu hexagoane albe și pentagoane negre. De asemenea, domurile geodezice au geometrii similare.
Construcție și dimensiuni[modificare | modificare sursă]


Acest poliedru poate fi construit dintr-un icosaedru prin trunchierea celor 12 vârfuri astfel încât din fiecare latură să fie tăiată câte o treime, la ambele capete. Acest lucru creează 12 fețe noi pentagonale și transformă cele 20 de fețe triunghiulare inițiale în hexagoane regulate. Astfel lungimea laturilor este de o treime din cea a laturilor inițiale. În plus, forma are 1440 de diagonale.
Coordonate carteziene[modificare | modificare sursă]
Coordonatele carteziene ale vârfurilor unui icosaedru trunchiat cu lungimea laturilor de 2[2] sunt permutările a:
- (0, ±1, ±3φ)
- (±1, ±(2 + φ), ±2φ)
- (±φ, ±2, ±(2φ + 1))
unde φ = 1 + √52 este secțiunea de aur. Raza circumscrisă este √9φ + 10 ≈ 4,956[2]
Dimensiuni[modificare | modificare sursă]

Dacă lungimea laturii icosaedrului trunchiat este a, raza unei sfere circumscrise (una care atinge icosaedrul trunchiat în toate vârfurile) este:
Acest rezultat este ușor de obținut folosind unul dintre cele trei dreptunghiuri ortogonale desenate în icosaedru (v. figura alăturată) ca punct de plecare. Unghiul dintre segmentele care unesc centrul și vârfurile conectate printr-o latură comună (calculat pe baza acestei construcții) este de aproximativ 23,281446°.
Aria și volumul[modificare | modificare sursă]
Aria A și volumul V al icosaedrului trunchiat cu lungimea laturii a sunt:
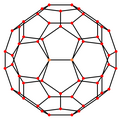
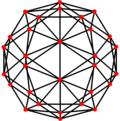
Proiecții ortogonale[modificare | modificare sursă]
Icosaedrul trunchiat are cinci proiecții ortogonale particulare, centrate: pe un vârf, pe două tipuri de muchii și pe două tipuri de fețe: hexagonale și pentagonale. Ultimele două corespund planelor Coxeter A2 și H2
| Centrată pe | Vârf | Latură 5-6 |
Latură 6-6 |
Față hexagon |
Față pentagon |
|---|---|---|---|---|---|
| Imagine | 
|

|

| ||
| Cadru de sârmă | 
|
|

|

|

|
| Simetrie proiectivă |
[2] | [2] | [2] | [6] | [10] |
| Dual | 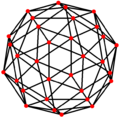
|
|

|

|

|
Pavări sferice[modificare | modificare sursă]

|
 centrată pe pentagon |
 centrată pe hexagon |
| Proiecții ortogonale | Proiecții stereografice | |
|---|---|---|
Icosaedrul trunchiat poate fi reprezentat și ca o pavare sferică și proiectat în plan printr-o proiecție stereografică. Această proiecție este conformă, conservând unghiurile, dar nu și ariile sau lungimile. Liniile drepte pe sferă sunt proiectate în plan ca arce de cerc.
Poliedre și pavări înrudite[modificare | modificare sursă]
| Familia de poliedre icosaedrice uniforme | |||||||
|---|---|---|---|---|---|---|---|
| Simetrie: [5,3], (*532) | [5,3]+, (532) | ||||||

|

|

|

|

|

|

|

|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duale ale poliedrelor uniforme | |||||||

|

|

|

|

| |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| Variante de simetrii *n32 ale pavărilor trunchiate: n.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sim. *n42 [n,3] |
Sferică | Euclid. | Compactă | Paracomp. | Hiperbolică necompactă | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| Figuri trunchiate |

|

|

|

|

|

|

|

|

|

|

| |
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| Figuri n-kis |

|

|

|

|

|

|

|

|
||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Aceste poliedre stelate uniforme și o stelare icosaedrică au anvelopa convexă de icosaedre trunchiate neuniforme:
 Icosaedru trunchiat neuniform 2 5 | 3 |
 U37 2 52 | 5 |
 U61 52 3 | 53 |
 U67 53 3 | 2 |
 U73 2 53 (32 54) |
 Stelarea completă |
 Icosaedru trunchiat neuniform 2 5 | 3 |
 U38 52 5 | 2 |
 U44 53 5 | 3 |
 U56 2 3 (5/4 52) | | ||
 Icosaedru trunchiat neuniform 2 5 | 3 |
 U32 | 52 3 3 |
Note[modificare | modificare sursă]
- ^ en Eric W. Weisstein, Uniform Polyhedron la MathWorld.
- ^ a b en Eric W. Weisstein, Icosahedral group la MathWorld.
Bibliografie[modificare | modificare sursă]
- en Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., ISBN: 0-486-23729-X. (Section 3-9)
- Cromwell, P. (). „Archimedean solids”. Polyhedra: "One of the Most Charming Chapters of Geometry". Cambridge: Cambridge University Press. pp. 79–86. ISBN 0-521-55432-2. OCLC 180091468.
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
 Materiale media legate de icosaedru trunchiat la Wikimedia Commons
Materiale media legate de icosaedru trunchiat la Wikimedia Commons- en Eric W. Weisstein, Truncated icosahedron la MathWorld.
- en Eric W. Weisstein, Archimedean solid la MathWorld.
- en Editable printable net of a truncated icosahedron with interactive 3D view
- en The Uniform Polyhedra
- en "Virtual Reality Polyhedra"—The Encyclopedia of Polyhedra
- en Klitzing, Richard. „3D uniform polyhedra”. Cheie: ti


