Poliedru regulat
Un poliedru regulat este un poliedru al cărui grup de simetrie acționează tranzitiv pe steagurile sale. Un poliedru regulat este extrem de simetric, fiind tranzitiv atât la nivel de vârfuri, cât și la nivel de muchii și fețe. În contextele clasice, sunt utilizate multe definiții echivalente diferite; una comună este că fețele sunt poligoane regulate congruente care sunt asamblate în același mod în jurul fiecărui vârf.
Un poliedru regulat este identificat prin simbolul Schläfli al formei {n,m}, unde n este numărul de laturi ale fiecărei fețe. iar m numărul fețelor care se întâlnesc în fiecare vârf. Există 5 poliedre regulate convexe finite (poliedrele platonice) și patru poliedre stelate (poliedrele Kepler–Poinsot), în total nouă poliedre regulate. În plus, există cinci compuși regulați ai poliedrelor regulate.
Poliedrele regulate
[modificare | modificare sursă]Există cinci poliedre regulate convexe, cunoscute sub numele de poliedre platonice, patru poliedre stelate regulate, poliedrele Kepler–Poinsot și cinci compuși regulați ai poliedrelor regulate.
Poliedrele platonice
[modificare | modificare sursă]Cele cinci poliedre platonice sunt cunoscute încă din antichitate.

|

|
|
|

|
| tetraedrul {3, 3} (Animație) |
cubul {4, 3} (Animație) |
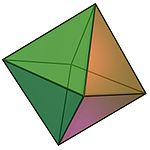
octaedrul {3, 4} (Animație) |
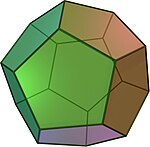
dodecaedrul {5, 3} (Animație) |
icosaedrul {3, 5} (Animație) |
| χ = 2 | χ = 2 | χ = 2 | χ = 2 | χ = 2 |
Poliedrele Kepler–Poinsot
[modificare | modificare sursă]Cele patru poliedre stelate regulate sunt cunoscute sub numele de poliedre Kepler–Poinsot.

|

|

|

|
| micul dodecaedru stelat {5/2, 5} (Animație) |
marele dodecaedru stelat {5/2, 3} (Animație) |
marele dodecaedru {5, 5/2} (Animație) |
marele icosaedru {3, 5/2} (Animație) |
| χ = −6 | χ = 2 | χ = −6 | χ = 2 |
Compușii regulați
[modificare | modificare sursă]
|

|
|

|

|
| două tetraedre 2 {3, 3} |
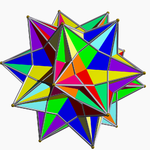
cinci tetraedre 5 {3, 3} (Animație) |
zece tetraedre 10 {3, 3} |
cinci cuburi 5 {4, 3} (Animație) |
cinci octaedre 5 {3, 4} |
| χ = 4 | χ = 10 |
Caracteristici
[modificare | modificare sursă]Proprietăți echivalente
[modificare | modificare sursă]Proprietatea de a avea un aranjament similar al fețelor în jurul fiecărui vârf poate fi înlocuită în definiții cu oricare dintre următoarele condiții echivalente:
- Vârfurile poliedrului se află toate pe o sferă.
- Toate unghiurile diedre ale poliedrului sunt egale.
- Toate figurile vârfurilor poliedrului sunt poligoane regulate.
- Toate unghiurile solide ale poliedrului sunt congruente.[1]
Sfere concentrice
[modificare | modificare sursă]Un poliedru regulat are toate cele trei sfere asociate care au același centru. La alte poliedre lipsește cel puțin una:
- sfera înscrisă în poliedru, tangentă la toate fețele;
- sfera mediană, tangentă la toate muchiile;
- sfera circumscrisă poliedrului, tangentă la toate vârfurile.
Simetrie
[modificare | modificare sursă]Poliedrele regulate sunt cele mai simetrice dintre toate poliedrele. Ele se află în doar trei grupuri de simetrie, care poartă numele poliedrelor platonice:
- tetraedric;
- octaedric (sau cubic);
- icosaedric (sau dodecaedric).
Orice forme cu simetrie octaedrică sau icosaedrică vor conține și simetria tetraedrică.
Caracteristica Euler
[modificare | modificare sursă]Caracteristica Euler este dată de relația:
unde V este numărul vârfurilor, M este numărul muchiilor, iar F este numărul fețelor.
Cele cinci poliedre platonice au o caracteristică Euler de 2. Acest lucru reflectă faptul că suprafața lor este o 2-sferă topologică, iar acest fapt este valabil și pentru orice poliedru stelat.
Puncte interioare
[modificare | modificare sursă]Suma distanțelor de la orice punct din interiorul unui poliedru regulat la muchii este independentă de poziția punctului (aceasta este o extensie a teoremei lui Viviani.) Cu toate acestea, afirmația inversă nu este valabilă nici măcar pentru tetraedre.[2]
Dualitatea poliedrelor regulate
[modificare | modificare sursă]Într-o pereche duală de poliedre vârfurile unui poliedru corespund fețelor celuilalt și invers.
Poliedrele regulate prezintă această dualitate după cum urmează:
- tetraedrul este autodual;
- cubul și octaedrul sunt unul dualul celuilalt;
- icosaedrul și dodecaedrul sunt unul dualul celuilalt;
- micul dodecaedru stelat și marele dodecaedru sunt unul dualul celuilalt;
- marele dodecaedru stelat și marele icosaedru sunt unul dualul celuilalt.
Diverse generalizări
[modificare | modificare sursă]În secolul al XX-lea au apărut o serie de generalizări ale ideii de poliedru regulat, ducând la câteva clase noi.
Poliedre regulate în spațiul neeuclidian și în alte spații
[modificare | modificare sursă]Studii despre spațiul neeuclidian (hiperbolic și eliptic) și alte spații precum spații complexe, descoperite în secolul precedent, au dus la descoperirea unor poliedre noi, cum ar fi poliedrele complexe, care ar putea lua forma geometrică regulată doar în acele spații.
Poliedre regulate în spațiul hiperbolic
[modificare | modificare sursă]
În spațiul hiperbolic H3, fagurii paracompacți regulați sunt pavați cu fațete euclidiene și au figuri ale vârfului ca la poliedrele finite. Astfel de pavări au un deficit unghiular care poate fi închis prin îndoire într-un sens sau altul. Dacă pavarea este dimensionată corespunzător, ea se va „închide” asimptotic la un singur punct ideal. Aceste pavări euclidiene sunt înscrise într-o orisferă la fel cum poliedrele sunt înscrise într-o sferă (care conține zero puncte ideale). Secvența se extinde atunci când pavările hiperbolice sunt ele însele utilizate ca fațete ale teselărilor hiperbolice necompacte, ca în fagurele pavat heptagonal {7,3,3}; ele sunt înscrise într-o suprafață echidistantă (un 2-hiperciclu), care are două puncte ideale.
Pavări regulate în planul proiectiv real
[modificare | modificare sursă]Un alt grup de poliedre regulate cuprinde pavările planului proiectiv real. Acestea includ hemicubul, hemioctaedrul, hemidodecaedrul și hemiicosaedrul. Ele sunt (la nivel global) poliedre proiective și sunt contrapartidele proiective ale poliedrelor platonice. Tetraedrul nu are un omolog proiectiv, deoarece nu are perechi de fețe paralele care pot fi contopite, așa cum au și celelalte patru poliedre platonice.
 hemicub {4, 3} |
 hemioctaedru {3, 4} |
 hemidodecaedru {3, 5} |
 hemiicosaedru {5, 3} |
Acestea apar ca perechi duale în același mod ca și poliedrele platonice. Caracteristicile lor Euler sunt toate 1.
Poliedre abstracte regulate
[modificare | modificare sursă]Până acum poliedrele erau ferm înțelese ca exemple tridimensionale de politopuri, mai generale, în orice număr de dimensiuni. A doua jumătate a secolului a cunoscut dezvoltarea unor idei algebrice abstracte precum combinatorica poliedrică, culminând cu ideea unui politop abstract ca mulțime parțial ordonată de elemente. Elementele unui poliedru abstract sunt corpul său (elementul maxim), fețele, muchiile, vârfurile și politopul nul (mulțimea vidă). Aceste elemente abstracte pot fi plasate în spațiul obișnuit sau realizate ca figuri geometrice. Unele poliedre abstracte au realizări bune, altele nu. Un steag este o mulțime conectată de elemente, câte una din fiecare dimensiune — pentru un poliedru care este corpul, o față, o latură a feței (muchie), un capăt al laturii (vârf) și politopul nul. Se spune că un politop abstract este regulat dacă simetriile sale combinatorii sunt tranzitive pe steagurile sale, adică orice steag poate fi translatat pe oricare altul conform simetriei poliedrului. Politopurile regulate abstracte rămân o zonă activă de cercetare.
Cinci astfel de poliedre regulate care nu pot fi realizate corect au fost identificate de Coxeter în cartea sa Regular Polytopes (1977) și din nou de J.M. Wills în articolul său "The combinatorially regular polyhedra of index 2" (1987). Toate cinci au simetrie C2×S5, dar pot fi realizate doar cu jumătate din simetrii, adică C2×A5 sau simetrie icosaedrică.[3][4][5] Toate sunt echivalente topologic cu toroizii. Construcția lor, prin aranjarea a n fețe în jurul fiecărui vârf, poate fi repetată la nesfârșit ca pavare a planului hiperbolic.
Poliedru 
triacontaedru rombic medial
dodecadodecaedru
icosaedru triambic medial
dodecadodecaedru ditrigonal
dodecaedru excavatTip dual {5,4}6 {5,4}6 dual de {5,6}4 {5,6}4 {6,6}6 (v,m,f) (24,60,30) (30,60,24) (24,60,20) (20,60,24) (20,60,20) Figura vârfului {5}, {5/2} 

(5.5/2)2 
{5}, {5/2} 

(5.5/3)3 

Fețe 30 romburi 
12 pentagoane
12 pentagrame

20 hexagoane 
12 pentagoane
12 pentagrame

20 hexagrame 
Pavaje 
{4, 5}
{5, 4}
{6, 5}
{5, 6}
{6, 6}χ −6 −6 −16 −16 −20
Duale Petrie
[modificare | modificare sursă]Dualul Petrie al unui poliedru regulat este o hartă regulată ale cărei vârfuri și muchii corespund vârfurilor și muchiilor poliedrului și ale cărui fețe sunt mulțimea poligoanelor strâmbe Petrie.[6]
| Nume | tetraedru Petrie | cub Petrie | octaedru Petrie | dodecaedru Petrie | icosaedru Petrie |
|---|---|---|---|---|---|
| Simbol Schläfli | {3, 3}π | {4, 3}π | {3, 4}π | {5, 3}π | {3, 5}π |
| (v,m,f), χ | (4,6,3), χ = 1 | (8,12,4), χ = 0 | (6,12,4), χ = −2 | (20,30,6), χ = −4 | (12,30,6), χ = −12 |
| Fețe | 3 pătrate strâmbe
|
4 hexagoane strâmbe | 6 decagoane strâmbe | ||

|

|

|

| ||
| Imagine | 
|

|

|

|

|
| Animație | 
|

|

|

|

|
| Figuri asociate |
 {4, 3}3 = {4, 3}/2 = {4, 3}(2,0) |
 {6, 3}3 = {6, 3}(2,0) |
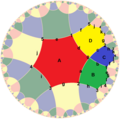 {6, 4}3 = {6, 4}(4,0) |
{10, 3}5 | {10, 5}3 |
Poliedre sferice
[modificare | modificare sursă]Cele nouă poliedre regulate pot fi, de asemenea, reprezentate ca pavări sferice:
 tetraedru {3, 3} |
 cub {4, 3} |
 octaedru {3, 4} |
 dodecaedru {5, 3} |
 icosaedru {3, 5} |
 micul dodecaedru stelat {5/2, 5} |
 marele dodecaedru {5, 5/2} |
 marele dodecaedru stelat {5/2, 3} |
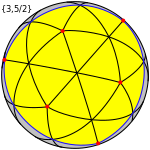 marele icosaedru {3, 5/2} |
Poliedre regulate care pot exista doar ca poliedre sferice
[modificare | modificare sursă]Pentru un poliedru regulat al cărui simbol Schläfli este {m, n}, numărul fețelor poligonale poate fi dat de:
Poliedrele platonice sunt singurele soluții întregi pentru m ≥ 3 și n ≥ 3. Restricția m ≥ 3 impune ca fețele poligonale trebuie să aibă cel puțin trei laturi.
Atunci când se consideră pavările sferice drept poliedre, această restricție poate fi relaxată, deoarece digoanele (2-gon) pot fi reprezentate ca fusuri sferice, având aria diferită de zero. Permiterea m = 2 admite o nouă clasă infinită de poliedre regulate, care sunt hosoedrele. Pe o suprafață sferică, poliedrul regulat {2, n} este reprezentat ca n fusuri adiacente, cu unghiuri interioare de 2π/n. Toate aceste fusuri se întâlnesc în două vârfuri comune.[7]
Un diedru, {n, 2}[7] (2-edru) în spațiul euclidian tridimensional poate fi considerat o prismă degenerată constând din două n-poligoane plane conectate „spate în spate”, astfel încât obiectul rezultat nu are grosime, analog modului în care un digon poate fi construit din două segmente alipite. Însă în pavările sferice un diedru poate exista sub formă nedegenerată, cu două fețe cu n laturi care acoperă sfera, fiecare față fiind o emisferă cu vârfuri în jurul unui cerc mare. Este regulat dacă vârfurile sunt egal distanțate.
 diedru digonal {2, 2} |
 diedru trigonal {3, 2} |
 diedru tetragonal {4, 2} |
 diedru pentagonal {5, 2} |
 diedru hexagonal {6, 2} |
... | {n, 2} |
 hosoedru digonal {2, 2} |
 hosoedru trigonal {2, 3} |
 hosoedru tetragonal {2, 4} |
 hosoedru pentagonal {2, 5} |
 hosoedru hexagonal {2, 6} |
... | {2, n} |
Hosoedrul {2, n} este dualul diedrului {n, 2}. De notat că dacă n = 2, se obține poliedrul {2, 2}, care este simultan un hosoedru și un diedru. Toate acestea au caracteristica Euler 2.
Note
[modificare | modificare sursă]- ^ en Cromwell, Peter R. (). Polyhedra. Cambridge University Press. p. 77. ISBN 0-521-66405-5.
- ^ en Chen, Zhibo, and Liang, Tian. "The converse of Viviani's theorem", The College Mathematics Journal 37(5), 2006, pp. 390–391.
- ^ en David A. Richter The Regular Polyhedra (of index two) Arhivat în , la Wayback Machine.
- ^ en Anthony M. Cutler, Egon Schulte, Regular Polyhedra of Index Two, I, 2010
- ^ en Regular Polyhedra of Index Two, II, Beitrage zur Algebra und Geometrie, 52(2):357–387, November 2010, Table 3, p. 27
- ^ en McMullen, Peter; Schulte, Egon (), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, 92, Cambridge University Press, p. 192, ISBN 9780521814966
- ^ a b Coxeter, Regular Polytopes, p. 12
Bibliografie
[modificare | modificare sursă]- fr Joseph Louis François Bertrand (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- de Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN: 3-7913-1990-6, (online)
- en Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- en Duncan MacLaren Young Sommerville (1930). An Introduction to the Geometry of n Dimensions E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- en H.S.M. Coxeter; Regular Polytopes (third edition). Dover Publications Inc. ISBN: 0-486-61480-8


















