Dodecaedru rombic
| Dodecaedru rombic | |
 | |
| (animație și model 3D) | |
| Descriere | |
|---|---|
| Tip | Poliedru Catalan |
| Fețe | 12 romburi |
| Laturi (muchii) | 24 |
| Vârfuri | 14 |
| χ | 2 |
| Configurația feței | V3.4.3.4 |
| Simbol Conway | jC |
| Diagramă Coxeter | |
| Grup de simetrie | Oh, B3, [4,3], (*432) |
| Grup de rotație | O, [4,3]+, (432) |
| Arie | ≈ 11,314 a2 (a = latura) |
| Volum | ≈ 3,079 a3 (a = latura) |
| Unghi diedru | 120° |
| Poliedru dual | Cuboctaedru |
| Proprietăți | Poliedru convex, tranzitiv pe fețe și pe laturi, paraleloedru, zonoedru |
| Desfășurată | |
 | |
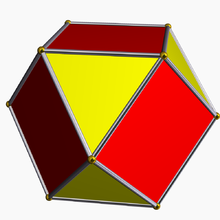
În geometrie un dodecaedru rombic este un poliedru Catalan cu 12 fețe congruente. Fiecare poliedru Catalan este dualul unui poliedru arhimedic. Este tranzitiv pe fețe și pe laturi
Proprietăți[modificare | modificare sursă]
Dodecaedrul rombic este un zonoedru. Dualul tetraedrului triakis este cuboctaedrul. Lungimea diagonalei lungi a feței este exact de √2 ori lungimea diagonalei scurte; astfel, unghiurile ascuțite de pe fiecare față măsoară arccos(13), adică aproximativ 70,53°.
Fiind dualul unui poliedru arhimedic, dodecaedrul rombic este tranzitiv pe fețe, adică grupul de simetrie al poliedrului acționează tranzitiv pe setul său de fețe. În termeni elementari, aceasta înseamnă că pentru oricare două fețe A și B, există o rotație sau reflexie a poliedrului care ocupă aceeași regiune a spațiului când fața A este aplicată pe fața B.
Dodecaedrul rombic poate fi perceput ca anvelopa convexă a reuniunii vârfurilor unui cub și ale unui octaedru. Cele 6 vârfuri unde se întâlnesc 4 romburi corespund vârfurilor octaedrului, în timp ce cele 8 vârfuri unde se întâlnesc 3 romburi corespund vârfurilor cubului.
Dodecaedrul rombic este unul dintre cele nouă poliedre convexe tranzitiv pe laturi, celelalte fiind cele cinci poliedre platonice, cuboctaedrul, icosidodecaedrul și triacontaedrul rombic.
Dodecaedrul rombic poate fi folosit pentru a tesela spațiu tridimensional: poate fi aranjat pentru a umple un spațiu tridimensional, la fel ca hexagonul umple un plan.
Acest poliedru într-o teselare de umplere a spațiului poate fi perceput ca o teselare Voronoi(d) a unei rețele cubice cu fețe centrate.
Un dodecaedru rombic poate fi divizat în 4 trapezoedre trigonale obtuze situate în jurul centrului său. Aceste romboedre sunt celulele unui fagure trapezoedric trigonal.
Dimensiuni[modificare | modificare sursă]
Se notează cu a lungimea laturii dodecaedrului rombic.
Raza sferei încrise (tangentă la toate fețele dodecaedrului rombic) este[1]
Raza sferei mediane este[2]
Raza sferei care trece prin cele 6 vârfuri de ordinul 4 (unde se întâlnesc câte patru fețe), dar nu și prin cele 8 vârfuri de ordinul 3 este[3]
Raza sferei care trece prin cele 8 vârfuri de ordinul 3 este exact de lungimea laturilor
Aria și volumul[modificare | modificare sursă]
Dacă laturile au lungimea a, aria și volumul dodecaedrului rombic sunt
Coordonate carteziene[modificare | modificare sursă]
 Variații piritoedrice între cub și dodecaedru rombic |
 Expandare a dodecaedrului rombic |
Cele opt vârfuri în care trei fețe se întâlnesc la unghiurile lor obtuze au coordonatele carteziene:
- (±1, ±1, ±1)
Coordonatele celor șase vârfuri unde patru fețe se întâlnesc la unghiurile lor ascuțite sunt:
- (±2, 0, 0), (0, ±2, 0) și (0, 0, ±2).
Dodecaedrul rombic poate fi văzut ca un caz limită degenerat al unui piritoedru, cu permutarea coordonatelor (±1, ±1, ±1) și (0, 1 + h, 1 − h2) cu parametrul h = 1.
Proiecții ortogonale[modificare | modificare sursă]
Dodecaedrul rombic are patru proiecții ortogonale particulare, de-a lungul axelor sale de simetrie, centrate pe față, pe latură și pe două tipuri de vârfuri, cu 3 și 4 poziții. Ultimele două corespund cu planele Coxeter B2 și A2.
| Simetrie proiectivă |
[4] | [6] | [2] | [2] |
|---|---|---|---|---|
| Dodecaedru rombic |

|

|

|

|
| Cuboctaedru (dual) |

|

|

|

|
Poliedre înrudite[modificare | modificare sursă]

| Poliedre octaedrice uniforme | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetrie: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||

|

|
 
|
 
|
 
|
 
|

|

|
 
| ||
| Dualele celor de mai sus | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |

|

|

|

|

|

|

|

|

|

|

|
Când sunt proiectate pe o sferă (v. figura din dreapta), se poate observa că laturile alcătuiesc laturile a două tetraedre dispuse în pozițiile lor duale (stella octangula). Această tendință continuă cu icositetraedrul deltoidal și hexecontaedrul deltoidal pentru perechile duale ale celorlalte poliedre regulate (împreună cu bipiramida triunghiulară dacă se iau în considerare pavările improprii), dând acestei forme denumirea sistematică alternativă de dodecaedru deltoidal.
| Simetrie *n32 [n,3] |
Sferice | Euclid. | Hiperb. compacte | Paracomp. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Config. feței |
 V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
 V3.4.∞.4 |
Acest poliedru este o parte dintr-o succesiune de poliedre rombice și pavări cu simetria [n,3] din grupul Coxeter. Cubul poate fi considerat un hexaedru rombic unde romburile sunt pătrate.
| Variante de pavări cvasiregulate duale: V(3.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| *n32 | Sferice | Euclidiană | Hiperbolice | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Pavare | 
|

|

|

|

|

|

| ||||
| Conf. | V(3.3)2 | V(3.4)2 | V(3.5)2 | V(3.6)2 | V(3.7)2 | V(3.8)2 | V(3.∞)2 | ||||
| Variante de pavări cvasiregulate duale: V(4.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetrie *4n2 [n,4] |
Sferică | Euclidiană | Hiperbolice compacte | Paracompactă | Necompactă | ||||||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[iπ/λ,4] | ||||
| Pavare Conf. |
 V4.3.4.3 |
 V4.4.4.4 |
 V4.5.4.5 |
 V4.6.4.6 |
 V4.7.4.7 |
 V4.8.4.8 |
 V4.∞.4.∞ |
V4.∞.4.∞ | |||
Similar, se înrudește cu seria infinită de pavări cu configurațiile fețelor V3.2n.3.2n, prima în planul euclidian, iar restul în planul hiperbolic.
 V3.4.3.4 (reprezentată ca desfășurată) |
 V3.6.3.6 Pavare euclidiană pavare rombică |
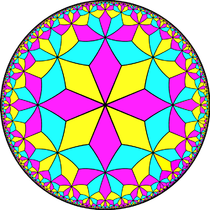 V3.8.3.8 Pavare hiperbolică (reprezentată în modelul discului Poincaré) |
Stelări[modificare | modificare sursă]

La fel cu multe poliedre convexe, dodecaedrul rombic poate fi stelat prin extinderea fețelor sau laturilor până când se întâlnesc pentru a forma un nou poliedru. Mai multe astfel de stelări au fost descrise de Dorman Luke.[4] Prima stelare, numită adesea simplu dodecaedrul rombic stelat, este binecunoscută. Poate fi considerată un dodecaedru rombic cu fiecare față augmentată prin atașarea unei piramide cu baza un romb, cu înălțimea piramidei astfel încât laturile să se afle în planele fețelor învecinate.
Luke mai descrie patru stelări: a doua și a treia stelare (expandându-se spre exterior), una formată prin îndepărtarea celei de-a doua dintr-a treia și alta prin adăugarea dodecaedrului rombic original înapoi la precedenta.
| Prima | A doua | A treia |
|---|---|---|
 Dodecaedrul rombic stelat |
 |
 Marele dodecaedru rombic stelat |
Note[modificare | modificare sursă]
- ^ Șirul A157697 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- ^ Șirul A179587 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- ^ Șirul A020832 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- ^ en Luke, D. (). „Stellations of the rhombic dodecahedron”. The Mathematical Gazette. 41 (337): 189–194. doi:10.2307/3609190. JSTOR 3609190.
Bibliografie[modificare | modificare sursă]
- en Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., ISBN: 0-486-23729-X. (Section 3-9)
- en Wenninger, Magnus (). Dual Models. Cambridge University Press. doi:10.1017/CBO9780511569371. ISBN 978-0-521-54325-5. MR 0730208. (The thirteen semiregular convex polyhedra and their duals, Page 19, Rhombic dodecahedron)
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008). The Symmetries of Things ISBN: 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, p. 285, Rhombic dodecahedron)
Legături externe[modificare | modificare sursă]
- en Eric W. Weisstein, Rhombic dodecahedron la MathWorld.
- en Eric W. Weisstein, Catalan solid la MathWorld.
- en Virtual Reality Polyhedra – The Encyclopedia of Polyhedra






