Cub snub
| Cub snub | |
  | |
| Cele două forme chirale, cw și ccw (animații cw și ccw, și model 3D) | |
| Descriere | |
|---|---|
| Tip | Poliedru arhimedic (poliedru uniform) |
| Fețe | 38 (8+24 triunghiuri, 6 pătrate) |
| Laturi (muchii) | 60 |
| Vârfuri | 24 |
| χ | 2 |
| Configurația vârfului | 3.3.3.3.4 |
| Simbol Wythoff | | 2 3 4 |
| Simbol Schläfli | sr{4,3} sau ht0,1,2{4,3} |
| Simbol Conway | sC |
| Diagramă Coxeter | |
| Grup de simetrie | Oh, 12B3, [4,3]+, (*432), ordin 24 |
| Grup de rotație | O, [4,3]+, (432), ordin 24 |
| Arie | ≈ 19,856 a2 (a = latura) |
| Volum | ≈ 7,889 a3 (a = latura) |
| Unghi diedru | 3-3: 153° 14′ 04″ (153,23°) 3-4: 142° 59′ 00″ (142,98°) |
| Poliedru dual | Icositetraedru pentagonal |
| Proprietăți | Poliedru semiregulat, convex, chiral |
| Figura vârfului | |
 | |
| Desfășurată | |
 | |

În geometrie cubul snub este un poliedru arhimedic. Are 38 de fețe, din care 8+24 triunghiulare și 6 pătrate, 24 de vârfuri și 60 de laturi.
Este un poliedru chiral, adică are două forme distincte, care sunt imagini în oglindă (sau „enantiomorfe”) una a celeilalte. Reuniunea ambelor forme dă compusul de două cuburi snub, iar anvelopa convexă al ambelor seturi de vârfuri este un cuboctaedru trunchiat.
Are indicele de poliedru uniform U12,[1] indicele Coxeter C24 și indicele Wenninger W17.
Johannes Kepler l-a denumit inițial în latină cubus simus în lucrarea sa Harmonices Mundi din 1619. H.S.M. Coxeter a remarcat că ar putea fi derivat în mod egal din octaedru, ca și cubul, numit „cuboctaedru snub”, cu simbolul Schläfli extins vertical , și reprezentând o alternare a unui cuboctaedru trunchiat, care are simbolul Schläfli .
Dimensiuni[modificare | modificare sursă]
Pentru un cub snub cu lungimea laturii 1, aria și volumul acestuia sunt:
unde t este constanta tribonacci
Dacă cubul snub inițial are lungimea laturii 1, dualul său, icositetraedrul pentagonal are lungimea laturii
- și .
Volumul unui cub snub cu lungimea laturii poate fi calculat cu relația:[2]
- ,
unde t este constanta tribonacci de mai sus.
Coordonate carteziene[modificare | modificare sursă]
Coordonatele carteziene ale vârfurilor unui cub snub centrat în origine sunt permutările pare ale
- (±1, ±1t, ±t)
cu un număr par de semne plus, împreună cu toate permutările impare cu un număr impar de semne plus, unde t ≈ 1,83929 este constanta tribonacci. Permutările pare cu un număr impar de semne plus și permutările impare cu un număr par de semne plus, dau un cub snub diferit, imaginea în oglindă a precedentului. Ambele împreună formează compusul de două cuburi snub.
Cu aceste coordonate lungimea laturilor cubului snub este , un număr care este o soluție a ecuației
și care poate fi scrisă ca
Pentru a obține un cub snub cu lungimea laturii 1, se împart toate coordonatele de mai sus cu valoarea α de mai sus.
Proiecții ortogonale[modificare | modificare sursă]

Cubul snub are două proiecții ortogonale particulare, centrate pe două tipuri de fețe: triunghiuri și pătrate, care corespund cu planele Coxeter A2 și B2 și una centrată pe mijlocul laturilor.
| Centrată pe |
Fața triunghi |
Fața pătrat |
Latură |
|---|---|---|---|
| Corp | 
|

|

|
| Cadru de sârmă | 
|

|

|
| Simetrie proiectivă |
[3] | [4]+ | [2] |
| Dual | 
|

|

|
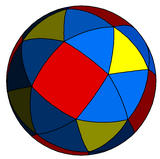
|
 centrată pe pătrat |
| Proiecție ortogonală | Proiecție stereografică |
|---|
Pavare sferică[modificare | modificare sursă]
Cubul snub poate fi reprezentat și ca o pavare sferică și proiectat pe plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu ariile sau lungimile. Liniile drepte (geodezicele) de pe sferă sunt proiectate în plan ca arce de cerc.
Relații geometrice[modificare | modificare sursă]
Cubul snub poate fi generat luând cele șase fețe ale cubului, deplasându-le spre exterior, apoi rotindu-le în jurul centrelor lor (toate în sensul acelor de ceasornic sau în sens invers) până când spațiile dintre pot fi umplute cu triunghiuri echilaterale.
Cubul snub poate fi derivat și din cuboctaedrul trunchiat prin procesul de alternare. 24 de vârfuri ale cuboctaedrului trunchiat formează un poliedru echivalent topologic cu cubul snub, celelalte 24 formează imaginea în oglindă. Poliedrul rezultat este tranzitiv pe vârfuri dar nu este uniform.
Un cub snub „îmbunătățit”, cu o față pătrată puțin mai mică și fețe triunghiulare puțin mai mari în comparație cu cubul snub uniform (poliedrul arhimedic), este util la reprezentările pe sferă.[3]
Poliedre înrudite[modificare | modificare sursă]
Cubul snub face parte dintr-o familie de poliedre uniforme înrudite cu cubul și octaedrul regulat.
| Poliedre octaedrice uniforme | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simetrie: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||

|

|
 
|
 
|
 
|
 
|

|

|
 
| ||
| Dualele celor de mai sus | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |

|

|

|

|

|

|

|

|

|

|

|
Variante de simetrii[modificare | modificare sursă]
Acest poliedru este înrudit topologic ca parte a secvenței de poliedre și pavări snub cu configurațiile vârfului (3.3.3.3.n.) și diagrama Coxeter–Dynkin ![]()
![]()
![]()
![]()
![]() . Aceste figuri și dualele lor au simetrie de rotație (n32) în notația orbifold, existând în planul euclidian pentru n = 6, iar în planul hiperbolic pentru orice n mai mare. Se poate considera că familia începe cu n = 2, care are fețele degenerate în digoane.
. Aceste figuri și dualele lor au simetrie de rotație (n32) în notația orbifold, existând în planul euclidian pentru n = 6, iar în planul hiperbolic pentru orice n mai mare. Se poate considera că familia începe cu n = 2, care are fețele degenerate în digoane.
| Variante de pavări snub cu simetrie n32: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simetrie n32 |
Sferice | Euclidiană | Hiperbolice compacte | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Imagini snub |

|

|

|

|

|

|

|

|
| Config. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Imagini giro |

|

|

|

|

|

|

|

|
| Config. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
Cubul snub este al doilea din seria poliedrelor și pavărilor snub cu configurația vârfului 3.3.4.3.n.
| Variante de pavări snub cu simetrie 4n2: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simetrie 4n2 |
Sferică | Euclidiană | Hiperbolice compacte | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Figuri snub |

|

|

|

|

|

|

|

|
| Config. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Figuri giro |

|

|

|

|
||||
| Config. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
Note[modificare | modificare sursă]
- ^ en Eric W. Weisstein, Uniform Polyhedron la MathWorld.
- ^ en „Snub Cube - Geometry Calculator”. rechneronline.de. Accesat în .
- ^ en / „Spherical Designs” de R.H. Hardin și N.J.A. Sloane
Bibliografie[modificare | modificare sursă]
- en Jayatilake, Udaya (martie 2005). „Calculations on face and vertex regular polyhedra”. Mathematical Gazette. 89 (514): 76–81. doi:10.1017/S0025557200176818.
- en Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., ISBN: 0-486-23729-X. (Section 3-9)
- en Cromwell, P. (). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
 Materiale media legate de cub snub la Wikimedia Commons
Materiale media legate de cub snub la Wikimedia Commons- en Eric W. Weisstein, Snub cube la MathWorld.
- en Eric W. Weisstein, Archimedean solid la MathWorld.
- en The Uniform Polyhedra
- en Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- en Editable printable net of a Snub Cube with interactive 3D view
- en Klitzing, Richard. „3D uniform polyhedra”. Cheie: snic







![{\displaystyle t={\frac {1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}}{3}}\approx 1,839\,286\,755\,21.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffc3b710235dbf4eca4f6a492bd66f787897dce7)






![{\displaystyle {\begin{aligned}\alpha &={\sqrt {{\frac {4}{3}}-{\frac {16}{3\beta }}+{\frac {2\beta }{3}}}}\approx 1,609\,72\\\beta &={\sqrt[{3}]{26+6{\sqrt {33}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/debe6a11001da1486aed45c37bbc75960a82fc23)





