Cuboctaedru

Descriere
Cuboctaedru

(animație și model 3D)
Tip	Poliedru arhimedic
Fețe	14 (8 triunghiuri, 6 pătrate)
Laturi (muchii)	24
Vârfuri	12
χ	2
Configurația vârfului	3.4.3.4
Simbol Wythoff	2 \| 3 4 3 3 \| 2
Simbol Schläfli	r{4,3} sau ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ rr{3,3} sau $r{\begin{Bmatrix}3\\3\end{Bmatrix}}$ t₁{4,3} sau t_0,2{3,3}
Simbol Conway	aC sau aaT
Diagramă Coxeter	sau sau
Grup de simetrie	O_h, B₃, [4,3], (*432), ordin 48
Grup de rotație	O, [4,3]⁺, (432), ordin 24
Arie	≈ 9,464 a² (a = latura)
Volum	≈ 2,357 a³ (a = latura)
Unghi diedru	125,26° = arcsec(−√3)
Poliedru dual	Dodecaedru rombic
Proprietăți	Poliedru cvasiregulat, convex cu fețe poligoane regulate, tranzitiv pe vârfuri și laturi
Figura vârfului

Desfășurată

În geometrie cuboctaedrul este un poliedru arhimedic. Are 14 fețe regulate (8 triunghiulare și 6 pătrate), 24 de laturi (muchii) identice, care fiecare sunt la limita dintre un triunghi și un pătrat. Are 24 de vârfuri, în fiecare întâlnindu-se două triunghiuri și două pătrate, care alternează. Ca atare, este un poliedru cvasiregulat, care nu este doar tranzitiv pe vârfuri, ci și tranzitiv pe laturi.^[1] Are și simetrie echilaterală radială.

Dualul său este dodecaedrul rombic.

Are indicele de poliedru uniform U₀₇,^[2] indicele Coxeter C₁₉ și indicele Wenninger W₁₁.

Proiectat într-o sferă, laturile unui coboctaedru definesc 4 cercuri mari, iar mijloacele laturilor și centrele triunghiurilor definesc alte 12 cercuri mari. Buckminster Fuller a folosit aceste 16 cercuri mari, împreună cu alte 9 din alt poliedru pentru a-și defini cele 25 de cercuri mari ale octaedrului sferic.

Cuboctaedrul era probabil cunoscut de Platon: în Definitiones Heron din Alexandria îl citează pe Arhimede spunând că Platon știa despre un corp format din 8 triunghiuri și 6 pătrate.^[3]

Sinonime[modificare | modificare sursă]

Cu simetria O_h, de ordin 48, este un cub rectificat sau un octaedru rectificat^[4]
Cu simetria T_d, de ordin 24, este un tetraedru cantelat sau un rombitetratetraedru.
Cu simetria D_3d, de ordin 12, este o girobicupolă triunghiulară.

Structură[modificare | modificare sursă]

Coordonate carteziene[modificare | modificare sursă]

Coordonatele carteziene ale vârfurilor unui cuboctaedru centrat în origine cu lungimea laturii √2 sunt^[5]

(±1, ±1, 0)

(±1, 0, ±1)

(0, ±1, ±1)

Un set alternativ de coordonate poate fi realizat în spațiul cvadridimensional ca 12 permutări ale

(0, 1, 1, 2)

Această construcție există ca fațetele dintr-unul din cele 16 ortante ale unui 16-celule cantelat.

Arie și volum[modificare | modificare sursă]

Aria A și volumul V ale unui cuboctaedru cu lungimea laturii a sunt:

{\begin{aligned}A&=\left(6+2{\sqrt {3}}\right)a^{2}&&\approx 9,464\,1016\,a^{2}\\V&={\tfrac {5}{3}}{\sqrt {2}}a^{3}&&\approx 2,357\,0226\,a^{3}.\end{aligned}}

Proiecții ortogonale[modificare | modificare sursă]

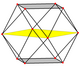
Cuboctaedrul are patru proiecții ortogonale, centrate pe un vârf, pe o latură și pe două tipuri de fețe: triunghiulare și pătrate. Ultimele două corespund cu planele Coxeter B₂ și A₂. Proiecțiile din poziții oarecare arată câte unul dintre pătratele, respectiv hexagoanele care trec prin centrul cuboctaedrului.

Proiecții ortogonale
Centrată pe fața pătrat	Centrată pe fața triunghi	Centrată pe vârf	Centrată pe latură


[4]	[6]	[2]	[2]
Dodecaedru rombic (poliedrul dual)

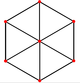
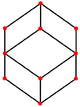
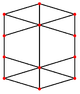
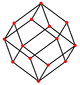
Pavare sferică[modificare | modificare sursă]

Cuboctaedrul poate fi reprezentat și ca o pavare sferică și proiectat pe plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu ariile sau lungimile. Liniile drepte pe sferă sunt proiectate în plan ca arce de cerc.

Proiecție ortogonală	Centrată pe pătrat	Centrată pe triunghi	Centrată pe vârf

Proiecție ortogonală	Proiecții stereografice

Divizare[modificare | modificare sursă]

Tetraedre și octaedre[modificare | modificare sursă]

Cuboctaedrul poate fi divizat în 6 piramide pătrate și 8 tetraedre, care se întâlnesc într-un punct central. Această divizare apare în fagurele tetraedric-octaedric unde perechile de piramide pătrate sunt combinate în octaedre.

Poliedre neregulate[modificare | modificare sursă]

Cuboctaedrul poate fi divizat în două cupole triunghiulare printr-un hexagon care trece prin centrul cuboctaedrului.^[a] Dacă aceste două cupole triunghiulare sunt rotite astfel încât triunghiurile și pătratele să se alinieze, se obține poliedrul Johnson J₂₇, o ortobicupolă triunghiulară.

Relații geometrice[modificare | modificare sursă]

Expandarea tetraedrului în cuboctaedru și expandarea înapoi la tetraedrul dual

Simetrie echilaterală radială[modificare | modificare sursă]

Într-un cuboctaedru raza lungă (de la centru până la vârf) are aceeași lungime cu latura; astfel diametrul său lung (de vârf la vârful opus) este de 2 lungimi de latură. Centrul său este ca apexul unei piramide: la distanță egală cu o latură de toate celelalte vârfuri. (În cazul cuboctaedrului, centrul este de fapt vârful a 6 piramide pătrate și 8 triunghiulare). Această simetrie echilaterală radială este o proprietate a doar câtorva politopuri uniforme, inclusiv hexagonul bidimensional, cuboctaedrul tridimensional și 24-celule și 8-celule (tesseractul) cvadridimensionale. Politopurile echilaterale radiale sunt cele care se pot construi, cu razele lor lungi, din triunghiuri echilaterale care se întâlnesc în centrul politopului, fiecare contribuind cu două raze și o latură. Prin urmare, toate elementele interioare care se întâlnesc în centrul acestor politopuri au fețe triunghiulare echilaterale spre interior, ca în divizarea cuboctaedrului în 6 piramide pătrate și 8 tetraedre.

Fiecare dintre aceste politopuri echilaterale radial apare, de asemenea, ca celule ale unei teselări caracteristice care umple spațiul: pavarea hexagonală regulată, fagurele cubic rectificat (cuboctaedre și octaedre alternativ), fagurele 24-celule și, respectiv, fagurele tesseractic. Fiecare teselare are o teselare duală; centrele celulelor dintr-o teselare sunt vârfuri ale celulelor în teselarea sa duală. Cea mai densă împachetare regulată a sferelor cunoscută în două, trei și patru dimensiuni folosește centrele celulelor ale uneia dintre aceste teselări ca centre ale sferelor.

Un cuboctaedru are simetrie octaedrică. Prima sa stelare este compusul de cub și octaedrul său dual, cu vârfurile cuboctaedrului situate la mijlocul laturilor fiecăruia.

Construcție[modificare | modificare sursă]

Așa cum un pătrat sau un hexahon pot fi contruite dintr-o secțiune ecuatorială printr-un cuboctaedru, un cuboctaedru poate fi construit dintr-o secțiune ecuatorială printr-un 16-celule sau un 24-celule.

Alte metode sunt rectificarea unui cub sau unui octaedru, sau cantelarea unui tetraedru.

Politopuri înrudite[modificare | modificare sursă]

Poliedre regulate[modificare | modificare sursă]

Cuboctaedrul face parte dintr-o familie de poliedre uniforme legate de cubul și octaedrul regulat.

Poliedre octaedrice uniforme v • d • m
Simetrie: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= sau	= sau	=

Dualele celor de mai sus
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Cuboctaedrul are și simetrie tetraedrică cu triunghiuri în două culori.

Familia poliedrelor tetraedrice uniforme
Simetrie: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duale ale poliedrelor uniforme

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Poliedre și pavări cvasiregulate[modificare | modificare sursă]

Cuboctaedrul există într-o succesiune de simetrii de poliedre și pavări cvasiregulate cu configurații ale vârfului (3.n)², de la pavări sferice la planul euclidian și planul hiperbolic. Cu notația orbifold a simetriei *n32 toate aceste pavări sunt construcții Wythoff într-un domeniu fundamental de simetrie, cu puncte generatoare în unghiul drept al domeniului. ^[6]^[7]

Pavări cvasiregulate cu simetrii orbifold *n32: (3.n)²
Construcție	Sferic			Euclidian	Hiperbolic
Construcție	*332	*432	*532	*632	*732	*832...	*∞32
Figuri cvasiregulate
Vârf	(3.3)²	(3.4)²	(3.5)²	(3.6)²	(3.7)²	(3.8)²	(3.∞)²

Variante de pavări cvasiregulate cu simetrie *n42: (4.n)²
Simetrie *4n2 [n,4]	Sferică	Euclidiană	Hiperbolice compacte				Paracompactă	Necompactă
Simetrie *4n2 [n,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[ni,4]
Imagini
Vârf	(4.3)²	(4.4)²	(4.5)²	(4.6)²	(4.7)²	(4.8)²	(4.∞)²	(4.ni)²

Acest poliedru este înrudit din punct de vedere topologic ca parte a secvenței de poliedre cantelate cu figurile vârfului (3.4.n.4) și continuă ca pavări ale planului hiperbolic. Aceste figuri tranzitive pe vârfuri au simetrie de reflexie *n32 în notația orbifold.

Variante de pavări expandate cu simetrie *n32: 3.4.n.4
Simetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paracomp.
Simetrie *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Imagine
Vârf	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

Politopuri cvadridimensionale[modificare | modificare sursă]

Cuboctaedrul poate fi descompus într-un octaedru regulat și opt octaedre neregulate, dar egale, în forma anvelopei convexe a unui cub cu două vârfuri opuse omise. Această descompunere a cuboctaedrului corespunde cu proiecția paralelă a primei celule a unui 24-celule în trei dimensiuni. Sub această proiecție, cuboctaedrul formează anvelopa proiecției, care poate fi descompusă în șase fețe pătrate, un octaedru regulat și opt octaedre neregulate. Aceste elemente corespund imaginilor a șase dintre celulele octaedrice din 24-celule, cele mai apropiate și cele mai îndepărtate celule din punctul de vedere cvadridimensional și, respectiv, restul de opt perechi de celule.

Note explicative[modificare | modificare sursă]

^ De reținut că cuboctaedrul are patru plane centrale hexagonale, înclinate la 60° față de celelalte. La fel cu hexagonul, cuboctaedrul poate fi împărțit în triunghiuri echilaterale care se întâlnesc în centrul său: are simetrie echilaterală radială.

Note[modificare | modificare sursă]

^ Coxeter 1973, pp. 18-19, §2.3 Quasi-regular polyhedra.
^ en Eric W. Weisstein, Uniform Polyhedron la MathWorld.
^ en Heath, Thomas Little (1931), „A manual of Greek mathematics”, Nature, Clarendon, 128 (3235): 739–740, Bibcode:1931Natur.128..739T, doi:10.1038/128739a0
^ După Norman Johnson
^ Coxeter 1973, p. 52, §3.7 Coordinates for the vertices of the regular and quasi-regular solids.
^ en Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN: 0-486-61480-8 (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction, pp.86–88)
^ en Two Dimensional symmetry Mutations by Daniel Huson

Bibliografie[modificare | modificare sursă]

en Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (ed. 3rd). New York: Dover.
en Weisstein, Eric W. (2002). „Cuboctahedron”. CRC Concise Encyclopedia of Mathematics (ed. 2nd). Hoboken: CRC Press. pp. 620–621. ISBN 9781420035223.
en Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., ISBN: 0-486-23729-X. (Section 3-9)
en Cromwell, P. (1997). „Archimedean solids”. Polyhedra: "One of the Most Charming Chapters of Geometry". Cambridge: Cambridge University Press. pp. 79–86. ISBN 0-521-55432-2. OCLC 180091468.