Teorema lui Pitagora

Suma catetelor la pătrat este egală cu ipotenuza la pătrat
| Geometrie |
|---|
 |
|
|
Cvadri- și n-dimensional |
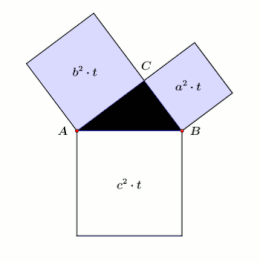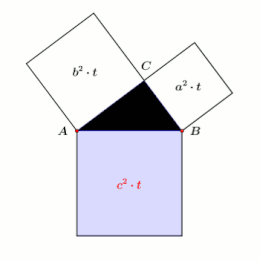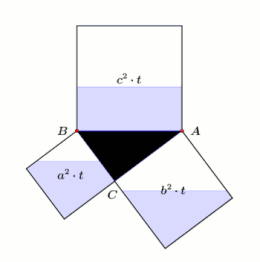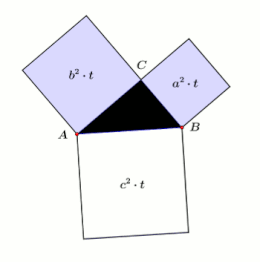
Teorema lui Pitagora este una dintre cele mai cunoscute teoreme din geometria euclidiană, constituind o relație între cele trei laturi ale unui triunghi dreptunghic. Teorema lui Pitagora afirmă că în orice triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei (latura opusă unghiului drept). Teorema poate fi scrisă sub forma unei relații între cele trei laturi a, b și c, câteodată denumită relația lui Pitagora:[1]
unde c reprezintă lungimea ipotenuzei, iar a și b lungimile celorlalte două laturi ale triunghiului.
Deși este în discuție faptul că teorema putea fi cunoscută dinaintea lui,[2] aceasta a fost totuși denumită după matematicianul din Grecia Antică, Pitagora (c. 570 – c. 495 î.Hr.) din moment ce el este cel care, în mod tradițional, a fost recunoscut pentru prima demonstrație a sa.[3][4] Există unele dovezi cum că matematicienii babilonieni ar fi înțeles formula, dar foarte puține indică o aplicație într-un cadru de lucru matematic.[5][6] Matematicienii din Mesopotamia, India și China au descoperit teorema independent și, în unele cazuri, au oferit demonstrații în cazuri speciale.
Această teoremă a primit numeroase demonstrații – probabil cele mai multe dintre toate teoremele din matematică. Acestea sunt foarte diversificate, incluzând dovezi atât geometrice cât și algebrice, cele mai vechi datând de acum mii de ani. Teorema poate fi generalizată în diferite moduri, inclusiv prin referire la spațiile multidimensionale, spațiile neeuclidiene, triunghiuri care nu sunt dreptunghice sau chiar figuri care nu sunt triunghiuri, ci spațiale.
Teorema lui Pitagora este considerată un punct de interes în afara matematicii, constituind un simbol al incomprehensibilității matematice, al misterului, sau al puterii intelectuale; abundă referințele populare din literatură, muzică, teatru, sau artă.
Istoric[modificare | modificare sursă]
Deși teorema i se atribuie astăzi filozofului și matematicianului grec antic Pitagora, care a trăit în secolul al VI-lea î.Hr., se știe că a fost cunoscută de mai multe civilizații de-a lungul timpului: indienii antici, asiro-babilonienii, egiptenii antici, chinezii antici și alții.[7]
Acest subiect poate fi împărțit în trei: cunoașterea tripletelor pitagoreice (seturi de câte trei numere întregi care reprezintă lungimile laturilor unui triunghi dreptunghic), cunoașterea teoremei propriu-zise și cunoașterea unor demonstrații.
Tripletele pitagoreice sunt cunoscute de foarte mult timp, ele fiind folosite pentru construirea unui unghi drept în condiții practice: o sfoară este marcată cu noduri aflate la anumite distanțe; formând din ea un triunghi (de exemplu de laturi 3, 4 și 5), acel triunghi va fi dreptunghic - metoda poate fi folosită de exemplu pentru a monta vertical catargul unui vas pe mare.
Monumente megalitice de acum 6000 de ani (în Egipt) sau 4500 de ani (în Insulele Britanice) conțin triunghiuri dreptunghice cu laturi de lungimi numere întregi[8], dar aceasta nu înseamnă neapărat că cei care le-au construit cunoșteau teorema. De asemenea, scrieri vechi din Regatul Mijlociu Egiptean și din Mesopotamia menționează triplete pitagoreice.
Sulba Sutra lui Baudhayana, scrisă în secolul VIII î.Hr. în India, conține o listă de triplete pitagoreice descoperite algebric, un enunț al teoremei, precum și o demonstrație pentru un triunghi dreptunghic isoscel.
Sulba Sutra lui Apastamba (circa 600 î.Hr.) conține o demonstrație numerică a cazului general, calculând arii. Unii cercetători susțin că de aici s-ar fi putut inspira Pitagora, în timpul călătoriei sale în India.
Pitagora (aproximativ 580 î.Hr. - 495 î.Hr.) a folosit metode algebrice pentru a construi triplete pitagoreice, conform lui Proclus. Acesta a scris însă între anii 410 și 485 d.Hr., adică 9 secole mai târziu. După Sir Thomas L. Heath, teorema nu i-a fost atribuită lui Pitagora timp de cinci secole după perioada în care acesta a trăit. Totuși, atunci când autori cum ar fi Plutarh și Cicero au vorbit despre teoremă ca fiind „a lui Pitagora”, au făcut-o ca și cum acesta era un lucru binecunoscut și de necontestat.
În jurul anului 400 î.Hr., conform lui Proclus, Platon a dat o metodă de a determina triplete pitagoreice care combină algebra și geometria. Există o infinitate de astfel de triplete,forma lor generală fiind x=2uv, y=u2-v2, z=u2+v2, unde u și v sunt numere naturale oarecare, cu u>v. După aproximativ 100 de ani, Euclid a dat în cadrul lucrării Elemente prima demonstrație axiomatică a teoremei.
Scris între 500 î.Hr. și 200 d.Hr., textul chinezesc Chou Pei Suan Ching (周髀算经) conține o demonstrație vizuală a teoremei.
De fapt, nu numai că nu se poate ști cine a descoperit teorema, dar cercetătorii nu se pot pune de acord nici în privința întrebării dacă a fost descoperită o singură dată, ori independent în istorie de către mai multe civilizații.
Teorema este valabilă doar în geometria euclidiană, de aceea orice demonstrație folosește (uneori indirect sau mai puțin vizibil) axioma lui Euclid.
Demonstrații[modificare | modificare sursă]
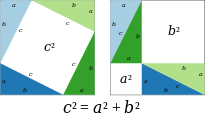
Teorema lui Pitagora a fost cunoscută mult timp înainte de Pitagora, dar el a fost primul care a demonstrat-o.[2] În orice mod, demonstrația atribuită lui este foarte simplă, și apelează la o rearanjare a figurilor.
Cele două pătrate mari reprezentate în figură conțin fiecare patru triunghiuri identice, iar singura diferență dintre cele două pătrate mari este faptul că triunghiurile sunt aranjate într-un mod diferit. Astfel, spațiul alb din interiorului fiecărui pătrat mare trebuie să aibă aceeași suprafață. Egalând suprafețele spațiilor albe reiese teorema lui Pitagora, c.c.t.d. [9]
Faptul că această demonstrație foarte simplă îi aparține lui Pitagora este dedus din scrierile filozofului și matematicianului grec Proclus.[10]
Este posibil ca aceasta să fie teorema cu cele mai multe demonstrații; cartea The Pythagorean Proposition (în traducere directă Propoziția Pitagorică) conține 370 de demonstrații.[11]
Demonstrația cu triunghiuri asemenea[modificare | modificare sursă]
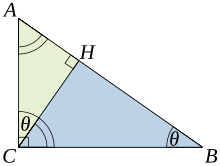
Această demonstrație are la bază proporționalitatea laturilor a două triunghiuri asemenea, adică are în vedere faptul că raportul dintre oricare două laturi corespondente ale triunghiurilor asemenea este aceeași, indiferent de mărimea triunghiurilor.
Fie ABC un triunghi dreptunghic, cu unghiul drept aflat în punctul C, după cum se observă în figură. Se desenează înălțimea în triunghi din punctul C, astfel ca H să fie punctul de intersecție al înălțimii cu latura AB. Punctul H împarte ipotenuza c în două părți, numite d și e. Noul triunghi, ACH, este asemenea cu triunghiul ABC, deoarece ambele au un unghi drept (prin definiție, înălțimea formează un unghi drept), iar unghiul lor comun este A, ceea ce înseamnă că cel de-al treilea unghi va fi același în ambele triunghiuri, marcat θ pe figură. Printr-o rațiune similară, triunghiul CBH este și el asemenea cu triunghiul ABC. Demonstrația asemănării triunghiurilor recurge la postulatul triunghiului: suma unghiurilor într-un triunghi este egală cu două unghiuri drepte, dar și la postulatul paralelismului. Asemănarea triunghiurilor ne conduce la egalarea raporturilor dintre laturile corespondente după cum urmează:
Primul rezultat este cosinusul unghiurilor θ, iar al doilea este sinusul lor.
Raporturile pot fi scrise astfel:
Însumarea acestor două egalități rezultă în
care, prin simplificare, dă expresia teoremei lui Pitagora:
Rolul acestei demonstrații de-a lungul istorie este subiectul multor speculații. Întrebarea care ar trebui pusă este de ce Euclid nu a folosit această demonstrație, dar a inventat alta. O presupunere ar fi că demonstrația cu triunghiuri asemenea avea nevoie de teoria proporțiilor, un subiect netratat până la publicarea lucrării Elemente, astfel că teoria proporțiilor avea nevoie de o dezvoltare mai mare la aceea vreme.[12][13]
Demonstrația lui Euclid[modificare | modificare sursă]

În mare parte, acesta este modul în care demonstrația lui Euclid din Elemente are loc. Pătratul mare este divizat în două dreptunghiuri, unul în stânga, iar altul în dreapta. Apoi, alt triunghi este construit astfel încât acesta să aibă jumătate din suprafața pătratului din partea stângă. Aceste două triunghiuri sunt congruente, ceea ce demonstrează faptul că acest pătrat are aceeași suprafață ca și dreptunghiul din stânga. O versiune analogă este valabilă și pentru dreptunghiul din partea dreaptă și pentru pătratul rămas. Recombinând cele două dreptunghiuri pentru a forma pătratul pe ipotenuză, suprafața sa este aceeași cu suma suprafețelor celor două pătrate. În continuare se află detaliile.
Fie A, B, C vârfurile unui triunghi dreptunghic, în care unghiul drept să fie A. Se trasează perpendiculara din punctul A prin ipotenuză, până pe latura opusă ipotenuzei, din pătrat. Dreapta desparte pătratul respectiv în două dreptunghiuri, fiecare având aceeași suprafață cu unul dintre pătratele de pe catete.
Pentru demonstrația formală, se recurge la patru leme elementare:
- Dacă un triunghi are două laturi egale cu alte două laturi ale unui alt triunghi, iar unghiurile făcute de aceste laturi sunt egale,
atunci triunghiurile sunt congruente.
- Suprafața unui triunghi este egală cu jumătate din suprafața oricărui paralelogram de aceeași bază și cu aceeași înălțime.
- Suprafața unui dreptunghi este egală cu produsul a două laturi adiacente.
- Suprafața unui pătrat este egală cu produsul a două dintre laturile sale (se deduce din 2).
În continuare, fiecare dintre pătratele de sus se află în legătură cu un triunghi congruent cu alt triunghi aflat la rândul său în legătură cu unul dintre cele două dreptunghiuri care alcătuiesc pătratul de jos.[14]
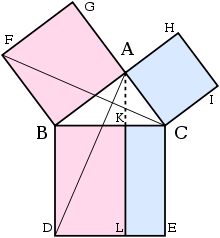
Demonstrația este următoarea:
- Fie ACB un triunghi dreptunghic cu unghiul drept CAB.
- Pe fiecare dintre laturile BC, AB și CA, se reprezintă pătratele CBDE, BAGF și ACIH, în această ordine. Construcția pătratelor necesită teoremele lui Euclid, și depinde de postulatul paralelismului.[15]
- Din A, se trasează dreapta paralelă cu BD și CE. Aceasta va fi perpendiculară pe laturile BC și DE, iar punctele de intersecție vor fi K și L.
- Se trasează dreptele CF și AD, formându-se triunghiurile BCF și BDA.
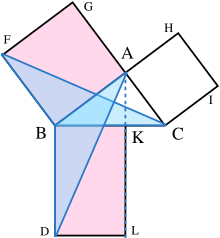
- Unghiurile CAB și BAG sunt ambele unghiuri drepte; astfel C, A, și G sunt puncte coliniare. Analog pentru punctele B, A și H.
- Unghiurile CBD și FBA sunt ambele unghiuri drepte; astfel ABD este egal cu unghiul FBC, din moment ce ambele sunt egale cu suma dintre un unghi drept și unghiul ABC:
- Deoarece AB este egală cu FB iar BD este egală cu BC, triunghiul ABD este congruent cu triunghiul FBC.
- Deoarece A-K-L este o dreptă, paralelă cu BD, atunci dreptunghiul BDLK este de două ori aria triunghiului ABD, având baza comună BD și înălțimea BK.
- Deoarece C este coliniar cu A și G, pătratul BAGF este de două ori aria triunghiului FBC.
- Astfel, dreptunghiul BDLK are aceeași arie ca pătratul BAGF = AB2.
- Similar, se poate arăta că dreptunghiul CKLE are aceeași arie cu pătratul ACIH = AC2.
- Adunând rezultatele putem scrie AB2 + AC2 = BD × BK + KL × KC
- Din moment ce BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Atunci AB2 + AC2 = BC2, pentru că CBDE este un pătrat.
Această demonstrație, care apare în Elementele lui Euclid, sub forma Propoziției 47 din Cartea 1,[16] arată faptul că suprafața pătratului de pe ipotenuză este suma suprafețelor celor două pătrate mici.[17] Această demonstrație este una destul de diferită față de cea folosind asemănarea triunghiurilor, care folosește posibila metoda de demonstrație a Pitagora.[13][18]
Demonstrația prin cvadratură[modificare | modificare sursă]
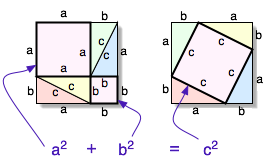
Suprafețele ambelor pătrate mari sunt egale cu . Dacă suprafețele pătratelor roz, ce reprezintă pătratele numerelor și (figura din stânga) sunt substituite cu un pătrat ce reprezintă numărul la pătrat, făcându-se simultan o rearanjare a jumătăților celor două dreptunghiuri (fiecare fiind format inițial din câte două triunghiuri dreptunghice, congruente cu cel inițial), se obține figura din dreapta. Suprafețele celor două pătrate mari sunt identice, întrucât laturile acestora sunt congruente.
Calculând în fiecare caz suprafețele celor două pătrate, se obține:
- (pentru pătratul din stânga)
- (pentru pătratul din dreapta)
Se ajunge așadar la , ceea ce duce direct la relația din teorema studiată.
Demonstrația prin rearanjare[modificare | modificare sursă]
Demonstrația pitagoreică, care a fost deja discutată, a fost o demonstrație prin rearanjare. Aceeași idee este reprezentată în animația din partea stângă, care conține pătratul mare de latură a + b, cu patru triunghiuri dreptunghice identice. Triunghiurile sunt reprezentate alternativ în două moduri de aranjare, în primul în care sunt arătate cele două pătrate mici a2 și b2, iar în al doilea în care este arătat pătratul c2. Suprafața cuprinsă de pătratul exterior nu se schimbă, iar suprafața celor patru triunghiuri este aceeași și la începutul rearanjării, dar și după, așadar suprafețele pătratelor negre sunt egale. Astfel, ajungem la rezultatul a2 + b2 = c2.
O a doua demonstrație prin rearanjare este reprezentată de animația din mijloc. Un pătrat mare este format din suprafața c2,din patru triunghiuri dreptunghice identice de laturi a, b și c, amplasate în jurul unui pătrat central mic. Apoi, se formează două dreptunghiuri cu laturile a și b prin mutarea triunghiurilor. Combinând pătratul mai mic cu aceste dreptunghiuri se formează două pătrate de suprafețe a2 și b2, care vor avea aceeași suprafață cu pătratul mare inițial.[19]
O a treia demonstrație este reprezentată în imaginea din dreapta. Pătratele superioare sunt divizate după cum se poate observa, în figuri cu nuanțe de albastru și verde, iar aceste figuri mici pot fi rearanjate pentru a umple pătratul mare inferior. Analog, acest lucru se poate face și invers. Astfel, se poate observa faptul că suprafața pătratului mare este egală cu suprafețele pătratelor mici.[20]
 |
 |
 |
Demonstrații algebrice[modificare | modificare sursă]
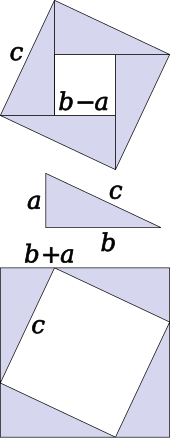
Teorema poate fi demonstrată algebric cu ajutorul a patru triunghiuri identice cu triunghiul dreptunghic de laturi a, b și c, aranjate în interiorul unui pătrat de latură c, după cum se poate observa în jumătatea superioară a diagramei.[21] Triunghiurile sunt congruente, având aria , în timp ce pătratul mic are latura b − a și aria (b − a)2. Așadar, aria pătratului mare este:
Dar acesta este un pătrat de latură c și cu suprafața c2, deci
O demonstrație similară folosește patru copii ale aceluiași triunghi, care sunt aranjate simetric în jurul unui pătrat de latură c, după cum se poate observa în partea inferioară a diagramei.[22] Astfel se formează un pătrat mai mare, de latură a + b și arie (a + b)2. Cele patru triunghiuri și pătratul de latură c au aceeași suprafață cu pătratul cel mare,
ceea ce conduce la:

O altă demonstrație, o variațiune a celor de mai sus, a fost publicată de președintele american James A. Garfield.[23][24] Diferența constă în utilizarea unui trapez în locul unui pătrat, acesta putând fi construit prin tăierea cu o dreaptă a pătratului mare reprezentat mai sus, în cadrul celei de-a doua demonstrații algebrice. Astfel, se obține trapezul reprezentat în diagramă. Deci suprafața trapezului este jumătate din cea a pătratului, adică
Folosindu-se ecuația pătratului mare, vom aveam rezultatul înjumătățit pentru trapez. Raportul se reduce, astfel că în final rămâne relația pitagoreică.
Demonstrația cu diferențiale[modificare | modificare sursă]
Se poate ajunge la teorema lui Pitagora prin intermediul studiului modului în care schimbările într-o latură produc o schimbare în ipotenuză, iar pentru această demonstrație se apelează la calcului diferențial și integral.[25][26][27]
Triunghiul ABC este un triunghi drept, după cum se observă și în partea superioară a diagramei, iar BC este ipotenuza. În același timp, lungimile triunghiului sunt măsurate după cum se poate vedea în partea inferioară, cu ipotenuza de lungime y, latura AC de lungime x și latura AB de lungime a.
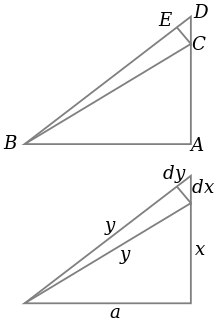
Dacă x crește cu o valoare mică dx prin extinderea laturii AC către D, atunci y de asemenea crește cu dy. Acestea formează două laturi ale unui triunghi, CDE, care (cu E ales astfel încât CE să fie perpendicular pe ipotenuză) este un triunghi dreptunghic aproximativ asemănător cu ABC. De aceea, raporturile dintre laturile lor trebuie să fie la fel, adică:
Asta poate fi rescris după cum urmează:
Aceasta este o ecuație diferențială care prin rezolvare dă
Iar constanta poate fi dedusă de la x = 0, y = a pentru a obține ecuația
Această demonstrație este mai degrabă intuitivă; se poate face și mai riguros dacă în locul valorilor dx și dy se folosesc limite.
Alte forme[modificare | modificare sursă]
După cum s-a arătat și în introducere, dacă c reprezintă lungimea ipotenuzei, iar a și b reprezintă lungimile celorlalte două laturi, teorema lui Pitagora poate fi exprimată sub forma unei relației pitagorice:
Dacă sunt cunoscute lungimile ambelor catete a și b , atunci c poate fi calculat astfel:
Dacă sunt cunoscute lungimea ipotenuzei c și a uneia dintre catete (a sau b), atunci lungimea celeilalte catete se poate calcula:
sau
Teorema lui Pitagora oferă o relație de legătură între laturile unui triunghi dreptunghic într-un mod simplu, astfel că dacă sunt cunoscute lungimile la două dintre laturi, se poate calcula lungimea celei de a treia. Un corolar al teoremei spune că în orice triunghi dreptunghic, ipotenuza este mai mare decât oricare dintre catete, dar mai mică decât suma acestora.
O generalizare a teoremei pitagorice este teorema cosinusului, care oferă posibilitatea de a calcula lungimea oricărei laturi a unui triunghi, dacă se cunosc lungimile a două dintre laturi și unghiul dintre ele. Dacă unghiul dintre ele două este un unghi drept, atunci această teoremă se reduce la relația pitagorică.
Reciproca[modificare | modificare sursă]
Reciproca teoremei este de asemenea adevărată:[28]
Oricare ar fi trei numere pozitive a, b, c astfel încât a2 + b2 = c2 , există un triunghi cu laturi de lungimi a, b, c, iar unghiul dintre laturile de lungimi a și b va fi drept.
O formulare alternativă a reciprocii este:
Pentru orice triunghi cu laturile a, b, c, dacă a2 + b2 = c2, atunci unghiul dintre laturile a și b are 90°.
Această reciprocă de asemenea apare în lucrarea Elemente a lui Euclid (Cartea I, Propoziția 48):[29]
"Dacă într-un triunghi pătratul unei dintre laturi este egal cu suma pătratelor laturilor rămas ale triunghiului, atunci unghiul dintre celelalte două laturi ale triunghiului este drept."
Poate fi demonstrată folosindu-se teorema cosinusului după cum urmează:
Fie ABC un triunghi cu laturile a, b și c cu proprietatea că a2 + b2 = c2. Fie un al doilea triunghi de lungime a și b, ce conține un unghi drept. Conform teoremei lui Pitagora, rezultă că ipotenuza acestui triunghi are lungimea laturii c = √a2 + b2, la fel cu ipotenuza primului triunghi. Din moment ce laturile ambelor triunghiuri au aceleași lungimi a, b și c, triunghiurile sunt congruente și trebuie să aibă aceleași unghiuri. Astfel, unghiul dintre laturile de lungime a și b din triunghiul original este un unghi drept.
Demonstrația reciprocii de mai sus face apel însuși la teorema lui Pitagora, dar reciproca poate fi demonstrată și fără să se utilizeze această teoremă.[30][31]
Un corolar ce derivă din reciproca teoremei lui Pitagora este o metodă simplă de a determina dacă un triunghi este dreptunghic, obtuzunghic sau ascuțitunghic. Fie c cea mai lungă dintre cele trei laturi și a + b > c (altfel nu există acest triunghi conform inegalității triunghiului). Atunci, sunt adevărate următoarele relații:[32]
- Dacă a2 + b2 = c2, atunci triunghiul este dreptunghic.
- Dacă a2 + b2 > c2, atunci triunghiul este ascuțitunghic.
- Dacă a2 + b2 < c2, atunci triunghiul este obtuzunghic.
Edsger Dijkstra a enunțat această propoziție despre triunghiul ascuțitunghic, obtuzunghic și dreptunghic în următorul limbaj matematic:
- sgn(α + β − γ) = sgn(a2 + b2 − c2),
unde α este unghiul opus laturii a, β este unghiul opus laturii b, γ este unghiul opus laturii c, iar sgn reprezintă funcția signum.[33]
Consecințe și utilizări[modificare | modificare sursă]
Triplete pitagoreice[modificare | modificare sursă]
Un triplet pitagoreic (sau numere pitagoreice) conține trei numere pozitive întregi a, b și c, astfel încât a2 + b2 = c2. Cu alte cuvinte, un triplet pitagoreic reprezintă lungimile laturilor unui triunghi dreptunghic astfel încât lungimile tuturor laturilor au valori numere întregi.[1][34] Observații asupra monumentelor megalitice din Europa Nordică arată evidențe ale faptului că aceste triplete erau cunoscute cu mult timp înainte de descoperirea scrisului. Un triplet scris în mod obișnuit este (a, b, c). Alte exemple bine-cunoscute sunt (3, 4, 5) și (5, 12, 13).
Un triplet pitagoreic primitiv este unul în care a, b și c sunt prime între ele (adică cel mai mare divizor comun al lui a, b și c este 1).
Următoarea este o listă de triplete pitagoreice primitive cu valori mai mici decât 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Lungimi incomensurabile[modificare | modificare sursă]

Una dintre urmările teoremei lui Pitagora este aceea că dreptele a căror lungimi sunt incomensurabile (adică raportul dintre ele nu este un număr rațional) pot fi construite cu ajutorul riglei și compasului. Teorema lui Pitagora oferă posibilitatea construirii unor segmente de lungimi incomensurabile deoarece ipotenuza unui triunghi este legată de operația numită rădăcină pătrată.
În figura din dreapta este ilustrat modul de construcție al unui segment a cărui lungime este rădăcina pătrată a oricărui număr întreg pozitiv, prin referire la alte două segmente.[35] Fiecare triunghi are o latură (numerotată cu 1) care este aleasă ca unitate de măsură. În fiecare dintre triunghiurile dreptunghice, teorema lui Pitagora stabilește lungimea ipotenuzei în conformitate cu unitatea. Dacă ipotenuza se calculează prin rădăcina pătrată a sumei catetelor (a căror valori sunt: unitatea iar alta orice număr natural) și suma nu este un pătrat perfect, atunci desenul ipotenuzei reprezintă trasarea unei lungimi incomensurabile. De exemplu, astfel sunt √2, √3, √5 .
Lungimile incomensurabile erau în conflict cu conceptele școlii pitagoreice, în care numai numerele întregi erau numere. Proporțiile erau realizate prin compararea multiplilor întregi a unei subunități comune.[36] Conform unei legende, Hippasos din Metaponte (ca. 470 î.Hr.) a fost înecat în mare pentru că a descoprit existența numerelor iraționale sau a incomensurabilității.[37][38]
Numere complexe[modificare | modificare sursă]

Pentru orice număr complex
valoarea absolută este dată de
Așadar cele trei numere, r, x și y sunt legate prin relația pitagoreică,
Trebuie menționat faptul că r este definit ca fiind un număr pozitiv sau zero, dar x și y pot fi sau negative sau pozitive. Din punct de vedere geometric, r este distanța lui z de la zero sau din punctul de origine O în planul complex.
Această relație poate fi generalizată pentru găsirea distanței dintre două punte, cum ar fi z1 și z2. Distanța căutată este dată de relația
care din nou este o versiune a relației pitagorice,
Distanțe euclidiene[modificare | modificare sursă]
Formula pentru distanță aplicabilă în coordonate carteziene este derivată din teorema lui Pitagora.[39] Dacă (x1, y1) și (x2, y2) sunt puncte dintr-un plan, atunci distanța dintre ele, de asemenea cunoscută și ca distanță euclidiană, este dată de formula:
Mai general, într-un spațiu euclidian de ordinul n, distanța euclidiană dintre două puncte, și , este definită, prin generalizarea teoremei lui Pitagora, ca:
Dacă nu sunt folosite coordonatele carteziene și, de exemplu, sunt folosite coordonate polare în două dimensiuni, formulele ce exprimă distanța euclidiană sunt mult mai complicate decât teorema lui Pitagora, dar pot fi derivate plecând de la aceasta. Un exemplu tipic în care distanța dintre două puncte este convertită în coordonate curbilinii poate fi găsit în cadrul aplicațiilor polinomialelor lui Legendre în fizică. Formulele pot fi deduse folosindu-se teorema lui Pitagora cu ecuațiile ce fac legătura dintre coordonatele curbilinii și cele carteziene. De exemplu, coordonatele polare (r, θ) pot fi scrise ca:
Cele două puncte cu locațiile (r1, θ1) și (r2, θ2) sunt separate de distanța s:
Combinând termeni și rezolvând diferite operații în pătrate, formula lui Pitagora în coordonate carteziene produce separarea în coordonate polare după cum urmează:
folosind formule pentru identitățile produselor prin sumă. Această formulă este cunoscută ca teorema cosinusului, câteodată numită și Teorema lui Pitagora Generalizată.[40]
Identitatea trigonometrică pitagoreică[modificare | modificare sursă]
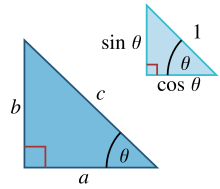
Într-un triunghi drept cu catetele a, b și ipotenuza c, din punct de vedere trigonometric sunt determinate sinusul și cosinusul unghiului θ dintre latura a și ipotenuză astfel:
De unde se deduce că:
unde ultima ecuație aplică teorema lui Pitagora. Această relație dintre sinus și cosinus este câteodată denumită identitatea trigonometrică pitagoreică fundamentală.[41] În triunghiuri asemenea, raportul dintre laturi este același indiferent de mărimile lor, și depinde de unghiuri. Astfel, în figură, triunghiul cu ipotenuza de mărime egală cu 1 are cateta opusă de mărimea sin θ și cateta alăturată de mărimea cos θ.
Produsul vectorial[modificare | modificare sursă]

Teorema lui Pitagora are o legătură strânsă și cu produsul vectorial și cu produsul scalar:[42]
Această relație poate fi privită prin definiția produsului vectorial și scalar ca:
unde n este un versor normal pentru a și b. Relația se deduce prin aceste definiții și prin identitatea trigonometrică pitagoreică.
Aceasta poate fi de asemenea definită și prin produs scalar. Prin rearanjarea ecuației următoare se obține:
Această relație poate fi considerată ca o condiție în produsul scalar și astfel parte din definiția sa.[43][44]
Generalizări[modificare | modificare sursă]
Figuri asemenea pe triunghiuri[modificare | modificare sursă]
O generalizare a teoremei lui Pitagora are la bază pătratele plasate pe un triunghi dreptunghic. Proprietățile referitoare la figurile asemenea plasate pe laturile unui triunghi erau cunoscute deja de Hipocrate din Chios din secolul V î.Hr.,[45] și a fost inclusă de Euclid în lucrarea sa, Elementele:[46]
Dacă cineva construiește figuri asemenea pe fiecare dintre laturile corespondente laturilor unui triunghi dreptunghi, atunci suma suprafețelor figurilor de pe laturile mici (catete) este egală cu suprafața figurii de pe latura mare (ipotenuză).
Această extindere asumă faptul că laturile triunghiului original sunt laturile corespondente ale celor trei figuri congruente (așadar raportul dintre laturile figurilor asemenea de pe triunghi este a:b:c).[47] Dacă demonstrația lui Euclid avea aplicabilitate numai pe poligoanele convexe, teorema se aplică de asemenea și poligoanelor concave și chiar figurilor asemenea cu margini curbe (dar care au o parte din figură legată de una dintre laturile triunghiului).[47]
Ideea de bază a acestei generalizări este aceea că suprafața unei figuri plane este proporțională cu pătratul oricărei dimensiuni liniare, și în particular este proporțională cu pătratul lungimii oricărei laturi. Astfel, dacă figurile asemenea de laturi A, B și C sunt construite cu lungimile corespunzătoare a, b și c, atunci:
Dar, conform teoremei lui Pitagora, a2 + b2 = c2, așadar A + B = C.
În schimb, dacă se poate demonstra faptul că este adevărată exoresia A + B = C pentru trei figuri asemenea fără să se folosească teorema lui Pitagora, atunci este posibil să se lucreze invers pentru a se realiza o demonstrație a teoremei. De exemplu, triunghiul central poate fi replicat și folosit ca un triunghi C pe ipotenuza sa, și două triunghiuri dreptunghice asemenea (A și B ) construite pe catetele sale, formate prin divizarea triunghiului central cu ajutorul înălțimii sale. Suma suprafețelor triunghiurilor mai mici este așadar egală cu suprafața celui de-al treilea triunghi, astfel A + B = C și inversând logica precedentă se ajunge la expresia teoremei lui Pitagora, a2 + b2 = c2.
 aria verde A + B = aria albastră C |
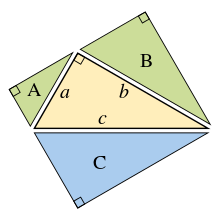 |
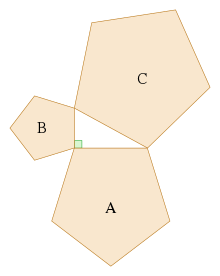 |
Triunghiuri oarecare[modificare | modificare sursă]

Se selectează orice unghi al unui triunghi oarecare de laturi a, b, c, și se înscrie acesta într-un triunghi isoscel astfel încât unghiurile egale de la baza sa, notate cu θ, sunt egale cu unghiul selectat anterior. Se presupune că unghiul selectat θ se opune laturii notate cu c. Prin înscrierea triunghiului isoscel se formează triunghiul ABD cu unghiul θ opus laturii a și cu latura r ce aparține de c. Un al doilea triunghi se formează cu unghiul θ opus laturii b și cu latura s ce aparține de c, conform figurii. Tâbit ibn Qorra[49] a spus că între laturile celor trei triunghiuri există următoarea relație:[50][51]
Pe măsură ce unghiul θ se apropie de π/2, baza triunghiului isoscel se micșorează, iar lungimile r și s se confundă tot mai mult, devenind un singur segment. Când θ = π/2, ADB devine un triunghi dreptunghic, r + s = c, ceea ce amintește de relația lui Pitagora.
O demonstrație punctează faptul că triunghiul ABC are aceleași unghiuri cu triunghiul ABD, dar în ordine inversă (cele două triunghiuri au un unghi comun în vârful B, ambele conțin unghiul θ, așadar au același al treilea unghi conform postulatului triunghiului). Prin urmare, ABC este asemenea cu reflexia lui ABD, adică triunghiul DBA din partea de jos a figurii. Considerând raportul laturilor opuse și adiacente lui θ, atunci
De asemenea, pentru reflexia celuilalt triunghi,
Prin calcule algebrice se ajunge la egalitatea:
rezultatul căutat.
Teorema rămâne validă dacă unghiul este obtuz iar lungimile r și s nu se suprapun.
Teorema cosinusului[modificare | modificare sursă]

Teorema lui Pitagora este un caz particular pentru o teorema mai generalizată care exprimă legături dintre laturile oricărui triunghi, numită teorema cosinusului sau, sugestiv, teorema lui Pitagora generalizată, care este exprimată astfel:[52]
unde θ este unghiul dintre laturile și .
Când θ este de 90 de grade, atunci cosθ = 0, astfel formula se reduce la simpla relație a lui Pitagora.
Geometrie spațială[modificare | modificare sursă]
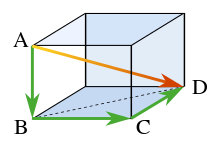

În stereometrie, sau geometrie spațială, teorema lui Pitagora poate fi aplicată în trei dimensiuni după cum urmează. Se consideră un solid dreptunghiular după cum se poate observa și în figură. Lungimea diagonalei BD se regăsește în teorema lui Pitagora astfel:
unde aceste trei laturi formează un triunghi dreptunghi. Folosind diagonala orizontală BD și latura verticală AB, lungimea diagonalei AD se găsește printr-o a doua aplicare a teoremei lui Pitagora astfel:
sau, dacă se face totul odată:
Acest rezultat este expresia tridimensională pentru magnitudinea unui vector v (diagonala AD) referindu-se la componentele lui ortogonale {vk} (cele trei laturi perpendiculare):
Această formulare scurtă poate fi privită ca o generalizare a teoremei lui Pitagora pentru dimensiuni mai mari. Totuși, acest rezultat este dat doar de aplicarea repetată a teoremei originale a lui Pitagora asupra unei succesiuni de triunghiuri dreptunghice într-o secvență de planuri ortogonale.
O generalizare substanțială a teoremei lui Pitagora în spațiul tridimensional este teorema lui De Gua, numită astfel după Jean-Paul de Gua de Malves: Dacă un tetraedru are un vârf format din unghiuri drepte (cum este colțul unui cub), atunci pătratul ariei feței opuse acestui vârf este egal cu suma pătratelor ariilor celorlalte trei fețe. Acest rezultat poate fi generalizat într-o așa-zisă teoremă a lui Pitagora n-dimensională:[53]
| “ | Fie vectori ortogonali pe ℝn. Se consideră simplexurile n-dimensionale S de vârfuri . (Se poate asemăna un simplex (n − 1)-dimensional de vârfuri , neincluzând originea, ca „ipotenuza” lui S și fețele rămase (n − 1)-dimensionale ale lui S ca și catetele sale). Atunci pătratului volumului ipotenuzei lui S este egal cu suma pătratelor volumelor „catetelor” n. | ” |
Această propoziție este ilustrată în trei dimensiuni cu ajutorul tetraedrului din figură. „Ipotenuza” este baza tetraedrului din spatele figurii, iar „catetele” sunt cele trei laturi care se întâlnesc în vârful din fața figurii. Pe măsură ce se mărește distanța dintre bază și vârf, la fel crește și suprafața „catetelor”, în timp ce cea a bazei rămâne fixă. Teorema sugerează faptul că atunci când această distanță atinge o valoare ce permite unghiuri drepte în jurul vârfului, generalizarea teoremei lui Pitagora are aplicabilitate. CU alte cuvinte:[54]
| “ | Pentru un simplex n-dreptunghiular și n-dimensional, pătratul conținutului (n − 1) feței opuse vârfului drept este egal cu suma pătratelor conținutului (n − 1) a fețelor rămase. | ” |
Spații prehilbertiene[modificare | modificare sursă]
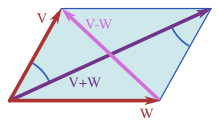
Teorema lui Pitagora poate fi generalizată în spațiile prehilbertiene, adică spații de produs vectorial,[55] care sunt generalizări ale spațiilor euclidiene bidimensionale și tridimensionale. De exemplu, o funcție poate fi considerată ca un vector cu un număr infinit de componente într-un spațiu prehilbertian, ca în analiza funcțională.[56]
Într-un spațiu prehilbertian, conceptul de perpendicularitate este înlocuit de conceptul de ortogonalitate doi vectori v și w sunt ortogonali dacă produsul lor scalar este zero. Spațiul prehilbertian, numit și spațiu de produs scalar, este o generalizare a produsului scalar dintre vectori.[57]
Conceptul de lungime este înlocuit de conceptul de normă ||v|| unui vector v, definită ca:[58]
Întru-un spațiu prehilbertian, teorema lui Pitagora spune că pentru oricare vectori ortogonali v și w avem
Aici, vectorii v și w sunt oarecum înrudiți cu laturile unui triunghi dreptunghic cu ipotenuza egală cu suma vectorială v + w. Această formă a teoremei lui Pitagora este o consecvență a proprietăților produsului scalar:
unde produsul scalar ar termenilor este zero, datorită ortogonalității.
O generalizare mai profundă a teoremei lui Pitagora legată de spațiile prehilbertiene, referitoare la vectorii neortogonali, este teorema paralelogramului:[58]
care spune că dublul sumei pătratelor lungimilor laturilor unui paralelogram este egal cu suma pătratelor lungimilor diagonalelor. Orice normă care satisface această egalitate este o normă corespondentă unui produs scalar.[58]
Identitatea pitagoreică poate fi extinsă la sume pentru mai mult de doi vectori ortogonali. Dacă v1, v2, ..., vn sunt vectori ortogonali perechi într-un spațiu prehilbertian, atunci aplicarea teoremei lui Pitagora pentru perechi succesive formate din acești vectori ia forma relației[59]
Geometrie neeuclidiană[modificare | modificare sursă]
Teorema lui Pitagora are la bază axiomele folosite în geometria euclidiană, dar, de fapt, ea nu are valabilitate în geometriile neeuclidiene.[60] (S-a arătat că teorema lui Pitagora este de fapt, echivalentă cu axioma paralelelor, adică al cincilea postulat al lui Euclid [61][62]). Cu alte cuvinte, în geometria neeuclidiană, relația dintre laturile unui triunghi trebuie să aibă o formă diferită de relația pitagoreică. De exemplu, în geometria sferică, toate cele trei laturi ale unui triunghi dreptunghic (cum ar fi a, b și c) au lungimea egală cu π/2, și toate unghiurile sale sunt drept, ceea ce se află în contradicție cu teorema lui Pitagora, deoarece a2 + b2 ≠ c2.
Mai jos sunt considerate două cazuri în geometrii neeuclidiene: sferică și hiperbolică. În fiecare caz, ca și în cazul euclidian pentru triunghiuri care nu sunt dreptunghice, rezultatul se află având ca punct de plecare teorema cosinusului.
Totuși, teorema lui Pitagora rămâne adevărată în geometriile hiperbolică și eliptică dacă și numai dacă suma a două unghiuri este egală cu al treilea, adică A+B = C. Laturile sunt apoi relaționate astfel: suma suprafețelor cercurilor de diametre a și b sunt egale cu diametrul c.[63]
Geometrie sferică[modificare | modificare sursă]

Pentru orice triunghi dreptunghic aflat pe o sferă de rază R (de exemplu, dacă γ din figură este un unghi drept), de laturi a, b, c, relația dintre laturi ia următoarea formă:[64]
Această relație poate fi dedusă ca un fiind caz special al teoremei cosinusului sferic, care se aplică tuturor triunghiurilor sferice:
Prin explicitarea seriilor Maclaurin pentru funcția cosinus ca o expansiune asimptotică,
se poate arăta faptul că în timp ce raza R se apropie de infinit și argumentele a/R, b/R și c/R tind către zero, relația sferică dintre laturile unui triunghi dreptunghic se apropie de forma euclidiană a teoremei lui Pitagora. Substituind expansiunea asimptotică pentru fiecare dintre cosinusuri în relația sferică pentru un triunghi dreptunghic se obține
Geometrie hiperbolică[modificare | modificare sursă]

Pentru un triunghi dreptunghic în geometria hiperbolică, cu laturile a, b, c iar c fiind latura opusă unghiului drept, relația dintre laturi ia următoarea formă:[65]
unde cosh este cosinusul hiperbolic. Această formulă este o formă specială a legii cosinusului hiperbolic care se aplică tuturor triunghiurilor hiperbolice:[66]
unde γ este unghiul format la vârful opus laturii c.
Folosind serii Maclaurin pentru cosinusul hiperbolic, cosh x ≈ 1 + x2/2, se poate arăta faptul că dacă un triunghi hiperbolic devine foarte mic (anume, când a, b și c tind spre zero), relația hiperbolică pentru un triunghi dreptunghic se apropie de teorema lui Pitagora.
Geometrie diferențială[modificare | modificare sursă]

La un nivel infinitezimal, în spațiul tridimensional, teorema lui Pitagora descrie distanța dintre două puncte separate infinitezimal ca:
unde ds este elementul distanței iar (dx, dy, dz) sunt componentele vectorului ce separă cele două puncte. Un asemenea spațiu se numește spațiu euclidian. Totuși, o generalizare a acestei expresii, folositoare pentru coordonate generale (nu doar carteziene) și spații generale (nu doar euclidiene) iau forma:[67]
unde gij se numește tensor metric. Poate fi o funcție de poziție. Astfel de spații curbe includ geometria lui Riemann ca exemplu general. Această formulare de asemenea se aplică unui spațiu euclidian când sunt folosite coordonate curbilinii. De exemplu, în coordonate polare:
În cultura populară[modificare | modificare sursă]

Teorema lui Pitagora se reflectă în cultura populară într-o mare varietate:
- Hans Christian Andersen a scris în 1831 un poem referitor la această teoremă: Formens Evige Magie (Et poetisk Spilfægteri).[68]
- Un vers din cântecul Major-General's Song de Gilbert și Sullivan din lucrarea de operă comică The Pirates of Penzance, "About binomial theorem I'm teeming with a lot o' news, With many cheerful facts about the square of the hypotenuse", face referire la teoremă.[69]
- Personajul Sperietoarea de ciori din filmul Vrăjitorul din Oz face o referire și mai specifică la teoremă, spunând o versiune greșită și distorsionată a acesteia: "The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side. Oh, joy! Oh, rapture! I've got a brain!"[70][71]
- În 2000, Uganda a emis o monedă în forma unui triunghi dreptunghic isoscel. Pe revers este reprezentată o imagine a lui Pitagora și relația α2 + β2 = γ2, împreună cu mențiunea "PYTHAGORAS MILLENNIUM".[72][73]
- Grecia, Japonia, San Marino, Sierra Leone și Surinam au emis mărci poștale cu referire la Pitagora și teorema sa.[74]
- În romanul de ficțiune speculativă a lui Neal Stephenson, Anathem, teorema lui Pitagora este denumită teorema Adrakhonică. O demonstrație a teoremei este proiectată pe o laterală a unei nave extraterestre pentru a demonstra înțelegerea matematică a extratereștrilor.
Note[modificare | modificare sursă]
- ^ a b Judith D. Sally, Paul Sally (). „Chapter 3: Pythagorean triples”. Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. p. 63. ISBN 0-8218-4403-2.
- ^ a b Posamentier, Alfred. The Pythagorean Theorem: The Story of Its Power and Beauty, p. 23 (Prometheus Books 2010).
- ^ George Johnston Allman (). Greek Geometry from Thales to Euclid (ed. Reprinted by Kessinger Publishing LLC 2005). Hodges, Figgis, & Co. p. 26. ISBN 1-4326-0662-X.
The discovery of the law of three squares, commonly called the "theorem of Pythagoras" is attributed to him by – amongst others – Vitruvius, Diogenes Laertius, Proclus, and Plutarch ...
- ^ (Heath 1921, Vol I, p. 144)
- ^ Otto Neugebauer (). The exact sciences in antiquity (ed. Republication of 1957 Brown University Press 2nd). Courier Dover Publications. p. 36. ISBN 0-486-22332-9.. For a different view, see Dick Teresi (). Lost Discoveries: The Ancient Roots of Modern Science. Simon and Schuster. p. 52. ISBN 0-7432-4379-X., where the speculation is made that the first column of tablet 322 in the Plimpton collection supports a Babylonian knowledge of some elements of trigonometry. That notion is pretty much laid to rest, however, by Eleanor Robson (). „Words and Pictures: New Light on Plimpton 322”. The American Mathematical Monthly. Mathematical Association of America. 109 (2): 105–120. doi:10.2307/2695324. JSTOR 2695324. (pdf file Arhivat în , la Wayback Machine.). The generally accepted view today is that the Babylonians had no awareness of trigonometric functions. See also Abdulrahman A. Abdulaziz (). „The Plimpton 322 Tablet and the Babylonian Method of Generating Pythagorean Triples”. arXiv:1004.0025
 [math.HO]. §2, page 7.
[math.HO]. §2, page 7.
- ^ Mario Livio (). The golden ratio: the story of phi, the world's most astonishing number. Random House, Inc. p. 25. ISBN 0-7679-0816-3.
- ^ Pythagorean Triangles and Triples - Mathematics and the Liberal Arts
- ^ „Megalithic triangles”. Arhivat din original la . Accesat în .
- ^ Benson, Donald. The Moment of Proof : Mathematical Epiphanies, pp. 172–173 (Oxford University Press, 1999).
- ^ Maor, Eli. The Pythagorean Theorem: A 4,000-year History, p. 61 (Princeton University Press, 2007).
- ^ (Loomis 1968)
- ^ (Maor 2007, p. 39) page 39
- ^ a b Stephen W. Hawking (). God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers. p. 12. ISBN 0-7624-1922-9. Această demonstrație a apărut pentru prima dată după ce un program de computer a fost programat să verifice demonstrațiile euclidiene.
- ^ De exemplu, vezi Teorema lui Pitagora Arhivat în , la Wayback Machine., Saint Louis University website Java applet
- ^ Jan Gullberg (). Mathematics: from the birth of numbers. W. W. Norton & Company. p. 435. ISBN 0-393-04002-X.
- ^ Elementele 1.47 de Euclid. Accesat pe 17 martie 2015.
- ^ Euclid's Elements, Book I, Proposition 47: web page version using Java applets from Euclid's Elements de Prof. David E. Joyce, Clark University
- ^ Demonstrația lui Pitagora a fost cel mai probabil nu una generală, din moment ce teoria proporțiilor a fost dezvoltată doar două secole după Pitagora; vezi și (Maor 2007, p. 25) pagina 25
- ^ Alexander Bogomolny. „Pythagorean Theorem, proof number 10”. Cut the Knot. Accesat în .
- ^ (Loomis 1968, Geometric proof 22 and Figure 123, page= 113)
- ^ Alexander Bogomolny. „Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3”. Cut the Knot. Accesat în .
- ^ Alexander Bogomolny. „Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4”. Cut the Knot. Accesat în .
- ^ Published in a weekly mathematics column: James A Garfield (). The New England Journal of Education. 3: 161. Lipsește sau este vid:
|title=(ajutor) as noted in William Dunham (). The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. Wiley. p. 96. ISBN 0-471-17661-3. and in A calendar of mathematical dates: 1 aprilie 1876 Arhivat în , la Wayback Machine. by V. Frederick Rickey - ^ Prof. David Lantz' animation from his web site of animated proofs
- ^ Mike Staring (). „The Pythagorean proposition: A proof by means of calculus”. Mathematics Magazine. Mathematical Association of America. 69 (1): 45–46. doi:10.2307/2691395. JSTOR 2691395.
- ^
Bogomolny, Alexander. „Pythagorean Theorem”. Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Accesat în . Legătură externa în
|work=(ajutor) - ^ Bruce C. Berndt (). „Ramanujan—100 years old (fashioned) or 100 years new (fangled)?”. The Mathematical Intelligencer. 10 (3): 24. doi:10.1007/BF03026638.
- ^ Judith D. Sally, Paul Sally (). „Theorem 2.4 (Converse of the Pythagorean Theorem).”. Cited work. p. 62. ISBN 0-8218-4403-2.
- ^ Euclid's Elements, Book I, Proposition 48 De la D.E. Joyce's web page la Clark University
- ^ Casey, Stephen, "The converse of the theorem of Pythagoras", Mathematical Gazette 92, July 2008, 309–313.
- ^ Mitchell, Douglas W., "Feedback on 92.47", Mathematical Gazette 93, March 2009, 156.
- ^ Ernest Julius Wilczynski, Herbert Ellsworth Slaught (). „Theorem 1 and Theorem 2”. Plane trigonometry and applications. Allyn and Bacon. p. 85.
- ^ „Dijkstra's generalization” (PDF).
- ^ Crâșmăreanu, Mircea. „Câteva probleme privind triplete pitagoreice” (pdf). Accesat în 13 martie. Parametru necunoscut
|anaccesare=ignorat (ajutor); Verificați datele pentru:|access-date=(ajutor) - ^ Law, Henry (). „Corollary 5 of Proposition XLVII (Pythagoras's Theorem)”. The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic. John Weale. p. 49.
- ^ Shaughan Lavine (). Understanding the infinite. Harvard University Press. p. 13. ISBN 0-674-92096-1.
- ^ (Heath 1921, Vol I, pp. 65); Hippasus was on a voyage at the time, and his fellows cast him overboard. See James R. Choike (). „The pentagram and the discovery of an irrational number”. The College Mathematics Journal. 11: 312–316.
- ^ O discuție detaliată despre contribuțiile lui Hippasos se găsesc în Kurt Von Fritz (). „The Discovery of Incommensurability by Hippasus of Metapontum”. Annals of Mathematics. Second Series. Annals of Mathematics. 46 (2): 242–264. JSTOR 1969021.
- ^ Jon Orwant, Jarkko Hietaniemi, John Macdonald (). „Euclidean distance”. Mastering algorithms with Perl. O'Reilly Media, Inc. p. 426. ISBN 1-56592-398-7.
- ^ Wentworth, George (). Plane Trigonometry and Tables. BiblioBazaar, LLC. p. 116. ISBN 1-103-07998-0., Exerciții, pagina 116
- ^ Lawrence S. Leff (). PreCalculus the Easy Way (ed. 7th). Barron's Educational Series. p. 296. ISBN 0-7641-2892-2.
- ^ WS Massey (). „Cross products of vectors in higher-dimensional Euclidean spaces”. The American Mathematical Monthly. Mathematical Association of America. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537.
- ^ Pertti Lounesto (). „§7.4 Cross product of two vectors”. Clifford algebras and spinors (ed. 2nd). Cambridge University Press. p. 96. ISBN 0-521-00551-5.[nefuncțională]
- ^ Francis Begnaud Hildebrand (). Methods of applied mathematics (ed. Reprint of Prentice-Hall 1965 2nd). Courier Dover Publications. p. 24. ISBN 0-486-67002-3.
- ^ Heath, T. L., A History of Greek Mathematics, Oxford University Press, 1921; reprinted by Dover, 1981.
- ^ Euclid's Elements: Book VI, Proposition VI 31: "In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle."
- ^ a b Putz, John F. and Sipka, Timothy A. "On generalizing the Pythagorean theorem", The College Mathematics Journal 34 (4), September 2003, pp. 291–295.
- ^ Howard Whitley Eves (). „§4.8:...generalization of Pythagorean theorem”. Great moments in mathematics (before 1650). Mathematical Association of America. p. 41. ISBN 0-88385-310-8.
- ^ Tâbit ibn Qorra (numele întreg Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826–901 AD) a fost un fizician ce a trăit în Bagdad și a scris o multitudine asupra Elementele lui Euclid și alte subiecte matematice.
- ^ Aydin Sayili (). „Thâbit ibn Qurra's Generalization of the Pythagorean Theorem”. Isis. 51 (1): 35–37. doi:10.1086/348837. JSTOR 227603.
- ^ Judith D. Sally, Paul Sally (). „Exercise 2.10 (ii)”. Roots to Research: A Vertical Development of Mathematical Problems. p. 62. ISBN 0-8218-4403-2.
- ^ Lawrence S. Leff (). cited work. Barron's Educational Series. p. 326. ISBN 0-7641-2892-2.
- ^ Rajendra Bhatia (). Matrix analysis. Springer. p. 21. ISBN 0-387-94846-5.
- ^ Pentru o discuție extinsă referitoare la această generalizare, vezi, de exemplu, Willie W. Wong Arhivat în , la Wayback Machine. 2002, A generalized n-dimensional Pythagorean theorem (engleză).
- ^ Ferdinand van der Heijden, Dick de Ridder (). Classification, parameter estimation, and state estimation. Wiley. p. 357. ISBN 0-470-09013-8.
- ^ Qun Lin, Jiafu Lin (). Finite element methods: accuracy and improvement. Elsevier. p. 23. ISBN 7-03-016656-6.
- ^ Howard Anton, Chris Rorres (). Elementary Linear Algebra: Applications Version (ed. 10th). Wiley. p. 336. ISBN 0-470-43205-5.
- ^ a b c Karen Saxe (). „Theorem 1.2”. Beginning functional analysis. Springer. p. 7. ISBN 0-387-95224-1.
- ^ Douglas, Ronald G. (). Banach Algebra Techniques in Operator Theory, 2nd edition. New York, New York: Springer-Verlag New York, Inc. pp. 60–1. ISBN 978-0-387-98377-6.
- ^ Stephen W. Hawking (). cited work. p. 4. ISBN 0-7624-1922-9.
- ^
Eric W. Weisstein (). CRC concise encyclopedia of mathematics (ed. 2nd). p. 2147. ISBN 1-58488-347-2.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
- ^
Alexander R. Pruss (). The principle of sufficient reason: a reassessment. Cambridge University Press. p. 11. ISBN 0-521-85959-X.
We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- ^ Victor Pambuccian (decembrie 2010). „Maria Teresa Calapso's Hyperbolic Pythagorean Theorem”. The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- ^ Barrett O'Neill (). „Exercise 4”. Elementary differential geometry (ed. 2nd). Academic Press. p. 441. ISBN 0-12-088735-5.
- ^ Saul Stahl (). „Theorem 8.3”. The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. p. 122. ISBN 0-86720-298-X.
- ^ Jane Gilman (). „Hyperbolic triangles”. Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0-8218-0361-1.
- ^ Tai L. Chow (). Mathematical methods for physicists: a concise introduction. Cambridge University Press. p. 52. ISBN 0-521-65544-7.[nefuncțională]
- ^ H.C. Andersen: Formens evige Magie (1831), visithcandersen.dk
- ^ Maor (2007), p. 47.
- ^ „The Scarecrow's Formula”. Internet Movie Data Base. Accesat în .
- ^ Singh, Simon. The Simpsons and Their Mathematical Secrets.
- ^ „Uganda 2000 Shillings”. Numismatic Guaranty Corporation. Accesat în .
- ^ „Le Saviez-vous?”. Arhivat din original la . Accesat în .
- ^ Miller, Jeff (). „Images of Mathematicians on Postage Stamps”. Accesat în .
Bibliografie[modificare | modificare sursă]
Engleză[modificare | modificare sursă]
- Bell, John L. (). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0.
- Euclid (). Translated by Johan Ludvig Heiberg with an introduction and commentary by Sir Thomas L. Heath, ed. The Elements (3 vols.). Vol. 1 (Books I and II) (ed. Reprint of 1908). Dover. ISBN 0-486-60088-2. On-line text at Euclid
- Heath, Sir Thomas (). „The 'Theorem of Pythagoras'”. A History of Greek Mathematics (2 Vols.) (ed. Dover Publications, Inc. (1981)). Clarendon Press, Oxford. p. 144 ff. ISBN 0-486-24073-8.
- Libeskind, Shlomo (). Euclidean and transformational geometry: a deductive inquiry. Jones & Bartlett Learning. ISBN 0-7637-4366-6. This high-school geometry text covers many of the topics in this WP article.
- Loomis, Elisha Scott (). The Pythagorean proposition (ed. 2nd). The National Council of Teachers of Mathematics. ISBN 978-0-87353-036-1. For full text of 2nd edition of 1940, see Elisha Scott Loomis. „The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs” (PDF). Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Accesat în . Originally published in 1940 and reprinted in 1968 by National Council of Teachers of Mathematics, isbn=0-87353-036-5.
- Maor, Eli (). The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Stillwell, John (). Mathematics and Its History. Springer-Verlag. ISBN 0-387-96981-0. Also ISBN 3-540-96981-0.
- Swetz, Frank; Kao, T. I. (). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China. Pennsylvania State University Press. ISBN 0-271-01238-2.
- van der Waerden, Bartel Leendert (). Geometry and Algebra in Ancient Civilizations. Springer. ISBN 3-540-12159-5.
- Alfred S. Posamentier: The Pythagorean Theorem: The Story of Its Power and Beauty. Prometheus Books 2010, ISBN 978-1-61614-181-3.
Alte limbi[modificare | modificare sursă]
- Anna M. Fraedrich: Die Satzgruppe des Pythagoras. Spektrum Akademischer Verlag, Heidelberg 1994, ISBN 3-86025-669-6.
- Hans Schupp: Elementargeometrie. UTB, Stuttgart 1977, ISBN 3-506-99189-2, S. 114–118.
- Alexander K. Dewdney: Reise in das Innere der Mathematik. Birkhäuser, Berlin 2000, ISBN 3-7643-6189-1, S. 47–76.
Legături externe[modificare | modificare sursă]
 Materiale media legate de teorema lui Pitagora la Wikimedia Commons
Materiale media legate de teorema lui Pitagora la Wikimedia Commons- The Pythagorean theorem: Teorema lui Pitagora (peste 70 de demonstrații ale teoremei, în engleză)
- Teorema lui Pitagora (în română)
- Legături interactive:
- Demonstrație interactivă în Java
- O altă demonstrație interactivă în Java
- Teorema lui Pitagora cu animație interactivă
- Animat, fără algebră Teorema lui Pitagora
- Subiect istoric: Teorema lui Pitagora în matematica babiloniană Arhivat în , la Wayback Machine.
- Hazewinkel, Michiel, ed. (), „Pythagorean theorem”, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Eric W. Weisstein, Pythagorean theorem la MathWorld.
- Euclid (David E. Joyce, ed. 1997) [c. 300 BC]. Elements. Accesat în 2006-08-30. Verificați datele pentru:
|date=(ajutor) In HTML with Java-based interactive figures.





































































![{\displaystyle 1-{\frac {1}{2}}\left({\frac {c}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)=\left[1-{\frac {1}{2}}\left({\frac {a}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)\right]\left[1-{\frac {1}{2}}\left({\frac {b}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right)\right]{\text{ când }}R\to \infty \ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6906ecded78c0d439f9f66eb1b2a6b6be10a299d)




