Trapez

Trapez

Trapezul (din greacă τραπέζια, transliterat: trapezia, „masă”) reprezintă un caz particular de patrulater convex, având două laturi opuse paralele și celelalte neparalele. Laturile paralele ale unui trapez se numesc baze. Distanța dintre cele două baze se numește înălțimea trapezului.

Trapezul isoscel are laturile neparalele congruente.

Trapezul dreptunghic are una din laturile neparalele perpendiculară pe cele două baze.

Trapezul oarecare are cele două laturi neparalele inegale și niciuna din ele nu formează unghi drept cu bazele.

Trapez isoscel

Trapez isoscel

Trapezul isoscel este un caz particular de trapez, care are laturile neparalele congruente.

Proprietăți

• unghiurile alăturate unei baze sunt congruente;
• unghiurile opuse sunt suplementare;
• diagonalele sunt congruente;
• în cazul în care diagonalele sunt perpendiculare, înălțimea este egală cu linia mijlocie, iar aria este egală cu pătratul înălțimii;
• poate fi considerat ca reuniunea unor paralelograme

Teoreme reciproce

• Dacă într-un trapez unghiurile alăturate unei baze sunt congruente atunci trapezul este isoscel.
• Dacă într-un trapez diagonalele sunt congruente atunci trapezul este isoscel.

Linia mijlocie într-un trapez

Linia mijlocie într-un trapez este egală cu media aritmetică a bazelor.

Divizarea unui trapez într-un dreptunghi și două triunghiuri.

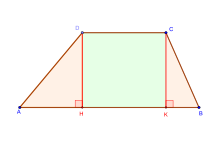
Acest enunț rezultă pe baza proprietăților liniei mijlocii într-un triunghi folosind o construcție ajutătoare sau prin echivalarea ariei trapezului cu a unui dreptunghi având ca laturi înălțimea și linia mijlocie a trapezului. Se folosește aici și divizarea trapezului într-un dreptunghi și două triunghiuri dreptunghice egale (în cazul trapezului isoscel) sau inegale, care au una dintre catete de aceeași lungime cu înălțimea trapezului.

Arie

Formula generală de calcul a ariei trapezului este dată de produsul dintre înălțime și semisuma celor două baze:

$A=h\cdot {\frac {a+b}{2}}$

sau: $A=h\cdot m$, unde $m$ este media aritmetică a bazelor: $m={\frac {a+b}{2}}.$