Teorema cosinusului

În geometria plană, teorema cosinusului, cunoscută și sub numele de teorema lui Pitagora generalizată stabilește relația dintre lungimea unei laturi a unui triunghi în funcție de celelalte două laturi ale sale și cosinusul unghiului dintre ele. Se găsește demonstrată și în Elementele lui Euclid (Propozițiile a 12-a și a 13-a din cartea a 2-a) într-o variantă de enunț care nu conține funcția trigonometrică cosinus, dar era cunoscută în formulare geometrică și de Hipocrate din Chios^[1].

Prin intermediul acestei teoreme se pot demonstra alte teoreme cum ar fi teorema lui Stewart, teorema paralelogramului, etc.

Enunț[modificare | modificare sursă]

Într-un triunghi oarecare pătratul unei laturi este egal cu suma pătratelor celorlalte două laturi minus de două ori produsul lor multiplicat cu cosinusul unghiului dintre ele.

În triunghi se face o construcție auxiliară trasând înălțimea din vârful unghiului avut în vedere.

BC^{2}=AB^{2}+AC^{2}-2AB\cdot AC\cos A\,

a^{2}=c^{2}+b^{2}-2cb\cos A\,

sau:

cos(BAC)={\frac {AB^{2}+AC^{2}-BC^{2}}{2AB*AC}}

unde AB=c, AC=b și BC=a sunt laturile triunghiului ABC.

Enunțul cunoscut de Hipocrate din Chios pentru un triunghi oarecare ABC cu D piciorul perpendicularei din vârful A pe latura BC este:

AB^{2}=BC^{2}+CA^{2}-2BC\cdot CD

Demonstrații[modificare | modificare sursă]

Euclid[modificare | modificare sursă]

Euclid utiliza în demonstrație Teorema lui Pitagora atât în cazul unghiului obtuz cât și în cel al unghiului ascuțit dintre două laturi ale unui triunghi pentru aflarea lungimii laturii a treia.

Cazul unghiului obtuz[modificare | modificare sursă]

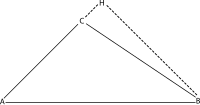
În scopul aflării lungimii laturii opuse unghiului obtuz, se duce segmentul CH perpendicular pe prelungirea unei laturi a unghiului obtuz, formându-se triunghiurile ( $AHB$ și $CHB$ ). Notând $d$ lungimea segmentului $CH$ și $h$ înălțimea $BH$ , teorema lui Pitagora în triunghiul dreptunghic $AHB$ dă

c^{2}=(b+d)^{2}+h^{2},

și triunghiul $CHB$ dă o egalitate care conține una din laturile alăturate unghiului obtuz ca ipotenuză

d^{2}+h^{2}=a^{2}.

Dezvoltarea primei egalități dă

c^{2}=b^{2}+2bd+d^{2}+h^{2}.

Substituind a doua egalitate se obține:

c^{2}=a^{2}+b^{2}+2bd.

sau cu notații ale segmentelor prin capete:

AB^{2}=CB^{2}+CA^{2}+2CA\cdot CH

Aceasta e Propoziția 12 din cartea a 2-a din Elemente referitoare la cazul unghiului obtuz.^[2]

Pentru transformare în forma actuală, a se vedea cosinusul pentru unghiuri suplementare:

d=a\cos(\pi -\gamma )=-a\cos \gamma =-CB\cdot cos(\gamma )

obținându-se

AB^{2}=CB^{2}+CA^{2}-2CA\cdot CB\cdot cos(\gamma )

Cazul unghiului ascuțit[modificare | modificare sursă]

Cazul unghiului ascuțit este prezentat similar în Propoziția a 13-a din cartea a 2-a, tot pe baza teoremei lui Pitagora. Aceasta se aplică în cele două triunghiuri dreptunghice ABH și AHC formate de înălțimea din punctul A pe baza BC care este astfel divizată în două segmente BH și HC a căror lungime însumată egalează lungimea lui BC, în acest scop considerându-se un triunghi dreptunghic arbitrar ales spre a include latura necunoscută, oricare din ele putând fi ales.

Se substituie pătratul înălțimii între cele două egalități date de teorema lui Pitagora și se ține cont și suma segmentelor determinate de înălțime pe latura opusă unghiului de unde pornește înălțimea.

În triunghiul ABH corespunzător laturii alese ca necunoscută are loc egalitatea

AB^{2}=BH^{2}+AH^{2}

În triunghiul AHC conținând unghiul opus laturii de aflat are loc egalitatea

CA^{2}=AH^{2}+HC^{2}

De aici se exprimă pătratul lungimii înălțimii AH

AH^{2}=CA^{2}-HC^{2}

care se înlocuiește în egalitatea din triunghiul ABH unde se substituie și lungimea segmentului BH ca diferență din lungimea laturii BC

BH=BC-HC

Se obține

AB^{2}=(BC-HC)^{2}+CA^{2}-HC^{2}

Se dezvoltă pătratul diferenței obținându-se

AB^{2}=BC^{2}+HC^{2}-2BC\cdot HC+CA^{2}-HC^{2}

în care se reduce pătratul lungimii segmentului HC și se obține egalitatea dorită

AB^{2}=BC^{2}+CA^{2}-2BC\cdot HC

Mai departe se poate exprima trigonometric lungimea segmentului HC:

HC=CA\cdot cos(\gamma )

.

Pe baza proprietăților cercului[modificare | modificare sursă]

Proprietățile cercului permit o demonstrație mai geometrică decât cea a lui Euclid.

Fig. a – triunghiul $ABC$ (roz), un cerc auxiliar (mov) și un triunghi dreptunghic auxiliar (galben)

Cazul unghiului ascuțit $γ$ , unde $a > 2 b cos γ$

Perpendiculara din $A$ pe $a$ = $BC$ , crează un segment de lungime $b cos γ$ . Prin duplicarea triunghiului dreptunghic se formează un triunghi isoscel $ACP$ . Construiește cercul cu centru $A$ și rază $b$ , și tangenta sa $h = BH$ prin $B$ . Tangenta $h$ formează un unghi drept cu raza $b$ (Elementele: Cartea a 3-a, Propoziția 18), astfel triunghiul galben e dreptunghic. Prin teorema lui Pitagora:

c^{2}=b^{2}+h^{2}.

Prin teorema tangentei secante (Elementele: Cartea a 3-a, Propoziția 36) care spune că pătratul pe tangenta printr-un punct $B$ exterior cercului e produsul celor două segmente (din $B$ ) create de orice secantă la cerc prin $B$ în cazul prezent: $BH 2 = BC \cdot BP$ sau

h^{2}=a(a-2b\cos \gamma ).

Substituind in egalitatea anterioară rezultă

c^{2}=b^{2}+a(a-2b\cos \gamma ).

A se nota că $h 2$ e puterea punctului $B$ în raport cu cercul. Folosirea teoremei lui Pitagora și a tangent-secantei poate fi înlocuită de o singură aplicare a teoremei puterii punctului.

Fig b – Triunghiul $ABC$ (roz), un cerc auxiliar (mov) și două triunghiuri dreptunghice auxiliare (galben)

Cazul unghiului ascuțit $γ$ , unde $a < 2 b cos γ$ .

Perpendiculara din $A$ pe $a$ = $BC$ , crează un segment de lungime $b cos γ$ . Prin duplicarea triunghiului dreptunghic se formează un triunghi isoscel $ACP$ . Construind cercul cu centru $A$ și rază $b$ și o coardă prin $B$ perpendiculară la $c = AB,$ jumătatea căreia e $h = BH$ prin teorema lui Pitagora se obține:

b^{2}=c^{2}+h^{2}.

Se utilizează apoi teorema coardelor (Elementele: Cartea a 3-a, Propoziția 35) despre produsul lungimilor segmentelor de pe o coardă intersectantă egal cu produsul celorlalte două segmente de pe cealaltă coardă:

În cazul acesta: $BH 2 = BC \cdot BP,$ sau

h^{2}=a(2b\cos \gamma -a).

Substituind în egalitatea anterioară dă:

b^{2}=c^{2}+a(2b\cos \gamma -a)\,.

În acest caz puterea punctului $B$ în raport cu cercul are valoarea negativă $- h 2$ .

Cazul unghiului obtuz $γ$

Demonstrație prin puterea punctului

În acest caz se utilizează puterea punctului direct, fără a apela la triunghiuri auxiliare bazate pe construcția vreunei tangente sau vreunei coarde.

Pentru un cerc cu centrul $B$ și raza $a$ (figura alăturată), care intersectează secanta prin $A$ și $C$ in $C$ și $K$ . Puterea punctului $A$ în raport cu cercul este egală și cu $AB 2 - BC 2$ și cu $AC \cdot AK$ . Așadar,

{\begin{aligned}c^{2}-a^{2}&{}=b(b+2a\cos(\pi -\gamma ))\\&{}=b(b-2a\cos \gamma ),\end{aligned}}

Prin utilizarea unor valori algebrice pentru lungimea segmentelor (incluzând numere negative pentru lungimi de segmente) se pot trata simultan cazurile unghiului ascuțit și al celui obtuz.

Prin teorema lui Pitagora și funcții trigonometrice[modificare | modificare sursă]

Se construiește înălțimea din unul din vârfurile laturii $c$ , la fel ca în figura de la secțiunea Enunț.^[3]. Fără a restrânge generalitatea, se construiește înălțimea corespunzătoare laturii $b$ . Se formează astfel două triunghiuri dreptunghice.

În triunghiul având ca ipotenuză latura $c$ , se aplică teorema lui Pitagora, apoi se folosește identitatea trigonometrică: $\quad \cos ^{2}\gamma +\sin ^{2}\gamma =1.$

${\begin{aligned}\quad c^{2}&=(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}\\&=b^{2}-2ab\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\&=b^{2}+a^{2}-2ab\cos \gamma ,\end{aligned}}$

Note[modificare | modificare sursă]

^ Mihăileanu, p. 29, 87, vol. I
^ Java applet version de Prof. D E Joyce of Clark University.
^ Küstner, Hellwitch, Kästner, Petite encyclopédie des mathématiques, Édition Didier, 1980, ch 11-2, p 265

Bibliografie[modificare | modificare sursă]

Nicolae N. Mihăileanu, Istoria matematicii, vol. 1, Editura Științifică și enciclopedică, București, 1974

Materiale media legate de Teorema cosinusului la Wikimedia Commons

[1] Mihăileanu, p. 29, 87, vol. I

[Joyce-2] Java applet version de Prof. D E Joyce of Clark University.

[3] Küstner, Hellwitch, Kästner, Petite encyclopédie des mathématiques, Édition Didier, 1980, ch 11-2, p 265

[1]

[2]

[3]