Tesseract
| Tesseract 8-celule 4-cub | |
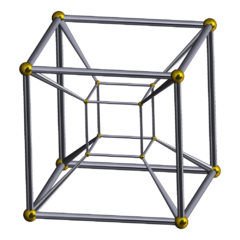 Diagramă Schlegel (vârfuri și laturi) | |
| Tip | 4-politop regulat convex |
|---|---|
| Simbol Schläfli | {4,3,3} t0,3{4,3,2} sau {4,3}×{ } t0,2{4,2,4} sau {4}×{4} t0,2,3{4,2,2} sau {4}×{ }×{ } t0,1,2,3{2,2,2} sau { }×{ }×{ }×{ } |
| Diagramă Coxeter | |
| Celule | 8 {4,3} |
| Fețe | 24 {4} |
| Laturi | 32 |
| Vârfuri | 16 |
| Figura vârfului |  Tetraedru |
| Poligon Petrie | octogon |
| Grup Coxeter | B4, [3,3,4] |
| Dual | 16-celule |
| Proprietăți | convex, izogonal, izotoxal, izoedric |
| Index uniform | 10 |

În geometrie un tesseract este un obiect din spațiul cu patru dimensiuni, fiind analogul 4-dimensional al cubului din trei dimensiuni și al pătratului din două dimensiuni.[2] La fel cum suprafața cubului este formată din șase fețe pătrate, hipersuprafața tesseractului este alcătuită din opt celule cubice. Tesseractul este unul dintre cele șase 4-politopuri regulate convexe.
Tesseractul mai este cunoscut drept 4-cub, 8-celule, C8[3] și prismă cubică. Este hipercubul 4-dimensional, parte a familiei de hipercuburi (a politopurilor de măsură).[4] Coxeter îl notează cu .[5] Termenul de "hipercub" fără a menționa dimensiunea este frecvent folosit ca sinonim pentru tesseract.
Conform Oxford English Dictionary, cuvântul „tesseract” a fost inventat și folosit pentru prima dată în 1888 de Charles Howard Hinton în cartea sa A New Era of Thought (în română O nouă eră de gândire). El provine din limba greacă τέσσερις ακτίνες (română patru raze), referindu-se la cele patru laturi care pleacă din fiecare vârf spre celelalte vârfuri.[6]
Geometrie[modificare | modificare sursă]
Tesseractul poate fi construit în mai multe moduri. Ca politop regulat cu trei cuburi pliate împreună în jurul fiecărei laturi, are simbolul Schläfli {4,3,3} cu simetria hiperoctaedrică de ordinul 384. Construit ca o hiperprismă 4D formată din două cuburi paralele, poate fi considerat un compus cu simbolul Schläfli {4,3} × { }, cu ordinul simetriei 96. Ca o duoprismă 4-4, un produs cartezian a două pătrate, poate fi descris printr-un simbol Schläfli compus {4}×{4}, cu ordinul simetriei 64. Ca ortotop poate fi descris prin simbolul Schläfli compozit { } × { } × { } × { } sau { }4, cu ordinul simetriei 16.
Deoarece fiecare vârf al unui tesseract este adiacent la patru margini, figura vârfului tesseractului este un tetraedru regulat. Politopul dual al tesseractului se numește 16-celule regulat, cu simbolul Schläfli {3,3,4}, cu care poate fi combinat pentru a forma compusul din tesseract și 16 celule.
Tesseractul standard în 4-spațiul euclidian este dat de anvelopa convexă a punctelor (± 1, ± 1, ± 1, ± 1). Adică constă din puncte:
Un tesseract este delimitat de opt hiperplane (xi = ±1). Într-un tesseract fiecare pereche de hiperplane neparalele se intersectează pentru a forma 24 de fețe pătrate. Trei cuburi și trei pătrate se întâlnesc pe fiecare latură. Există patru cuburi, șase pătrate și patru laturi care se întâlnesc în fiecare vârf. Una peste alta, este format din 8 cuburi, 24 de pătrate, 32 de laturi și 16 vârfuri.
Proiecții în 2 dimensiuni[modificare | modificare sursă]
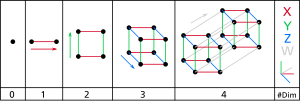

Un hipercub poate fi construit în modul următor:
- 1-dimensional: Două puncte A și B pot fi conectate pentru a deveni un segment de dreaptă AB.
- 2-dimensional: Două segmente de dreaptă paralele AB și CD pot fi conectate pentru a deveni un pătrat, cu colțurile marcate ABCD.
- 3-dimensional: Două pătrate paralele ABCD și EFGH pot fi conectate pentru a deveni un cub, cu colțurile marcate ABCDEFGH.
- 4-dimensional: Două cuburi paralele ABCDEFGH și IJKLMNOP pot fi conectate pentru a deveni un tesseract, cu colțurile marcate ABCDEFGHIJKLMNOP.
Este posibil ca tesseractul să fie proiectat în spațiile tridimensional și bidimensional, similar cu proiectarea unui cub în spațiul bidimensional.
Proiecțiile în 2D devin mai instructive prin rearanjarea pozițiilor vârfurilor proiectate. Astfel se pot obține imagini care deși nu mai reflectă relațiile spațiale din tesseract, ilustrează structura conexiunilor vârfurilor, cum ar fi în următoarele exemple.
Un tesseract se obține în principiu prin combinarea a două cuburi. Schema este similară cu construcția unui cub din două pătrate: se juxtapun două copii ale cubului cu dimensiuni inferioare și se conectează vârfurile corespunzătoare. Fiecare latură a unui tesseract are aceeași lungime. Această vizualizare prezintă interes atunci când se utilizează tesseractele ca baze într-o topologie de rețea în care sunt legate mai multe procesoare pentru calcul paralel: distanța dintre două noduri este de cel mult 4 și există multe căi diferite pentru a permite echilibrarea încărcării.
Proiecții paralele în 3 dimensiuni[modificare | modificare sursă]

Proiecția paralelă cu o celulă în față a tesseractului în spațiul tridimensional are o anvelopă cubică. Cea mai apropiat și cea mai îndepărtată celulă sunt proiectate pe cub, iar restul de șase celule sunt proiectate (degenerate în 3D) pe cele șase fețe pătrate ale cubului.
Proiecția paralelă cu o față în față a tesseractului în spațiul tridimensional are o anvelopă coboidă. Două perechi de celule se proiectează pe jumătățile superioare și inferioare ale acestei anvelope, iar cele patru celule rămase se proiectează pe fețele laterale.
Proiecția paralelă cu o latură în față a tesseractului în spațiul tridimensional are o anvelopă în formă de prismă hexagonală. Șase celule se proiectează pe prismele rombice, care sunt situate în prisma hexagonală într-un mod analog modului în care fețele cubului 3D se proiectează pe șase romburi într-un anvelopă hexagonală dintr-o proiecție cu un vârf în față. Cele două celule rămase se proiectează pe bazele prismei.
Proiecția paralelă cu un vârf în față a tesseractului în spațiul tridimensional are o anvelopă în formă de dodecaedru rombic. Două vârfuri ale tesseractului sunt proiectate în origine. Există două moduri de disecare a unui dodecaedru rombic în patru romboedre congruente, oferind un total de opt romboedre posibile, fiecare fiind proiecția unei celule a tesseractului. Această proiecție este cea cu volum maxim. Un set de vectori de proiecție sunt u = (1, 1, −1, −1), v = (−1, 1, −1, 1), w = (1, −1, −1, 1).
Galerie de imagini[modificare | modificare sursă]
- Proiecții în perspectivă
 Perspectivă cu eliminarea volumului ascuns. Colțul roșu este cel mai apropiat în 4D și în el se întâlnesc 4 celule cubice |
 Proiecție stereoscopică 3D a tesseractului (imaginea stereo apare fixând privirea „la infinit”) |
- Animații

|

|
| Proiecție 3D a unui tesseract executând o rotație simplă în planul care divide obiectul dinspre față–stânga spre spate–dreapta și de sus în jos | Proiecție 3D a unui tesseract executând o rotație în două plane ortogonale |
- Grafuri
 Dodecaedrul rombic formează anvelopa convexă a proiecției paralele cu un vârf în față. Numărul vârfurilor pe nivelele acestui graf este 1 4 6 4 1 — al cincilea rând din triunghiul lui Pascal |
 Tetraedrul formează anvelopa convexă a proiecției centrale centrată pe un vârf al tesseractului. Sunt prezentate patru din cele 8 celule cubice. Cel de-al 16-lea vârf este proiectat la infinit iar cele patru laturi care se întâlnesc în el nu sunt reprezentate. |
 Proiecție stereografică (laturile sunt proiectate pe o 3-sferă) |
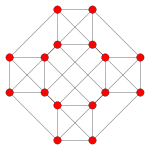
Proiecții ortogonale 2D[modificare | modificare sursă]


| Plan Coxeter | B4 | B3 / D4 / A2 | B2 / D3 |
|---|---|---|---|
| Graf | 
|

|

|
| Simetrie diedrală | [8] | [6] | [4] |
| Plan Coxeter | Altele | F4 | A3 |
| Graf | 
|
|

|
| Simetrie diedrală | [2] | [12/3] | [4] |
Simetrie echilaterală radială[modificare | modificare sursă]
Destanța de la centru la vârf a tesseractului este egală cu lungimea laturii sale; astfel diagonala sa prin centru (de la un vârf la vârful opus) este de 2 lungimi ale laturii. Numai câteva politopuri uniforme au această proprietate, inclusiv tesseractul și 24-celule, cuboctaedrul tridimensional și hexagon bidimensional. Tesseractul este singurul hipercub cu această proprietate. (Strict vorbind, hipercuburile cu 0 dimensiuni (un punct) și 1 dimensiune (un segment de dreaptă) sunt, de asemenea, echilaterale radial.) Cea mai lungă distanță vârf la vârf a unui n-hipercub cu lungimea muchiei egală cu unitatea este √n, deci pentru pătrat este √2, pentru cub este √3, iar numai pentru tesseract este √4, exact lungimea a două laturi.
Teselare[modificare | modificare sursă]
Tesseractul, ca toate hipercuburile, teselează spațiul euclidian. Fagurele tesseractic autodual format din 4 tesseracte în jurul fiecărei fețe are simbolul Schläfli {4,3,3,4}. Prin urmare, tesseractul are un unghi diedru de 90°.[7] Simetria echilaterală radială a tesseractului face ca teselarea sa să fie singura rețea cubică regulată centrată pe corp în orice număr de dimensiuni.
Tesseractul însuși poate fi descompus în politopuri mai mici. De exemplu, poate fi triangulat în 4-simplexuri care au aceleași vârfuri cu tesseractul. Se știe că există 92487256 astfel de triangulări[8] și că cel mai mic număr de 4-simplexuri din oricare dintre ele este 16.[9]
Poligon complex asociat[modificare | modificare sursă]
| Ortogonal | Perspectivă |
|---|---|

|

|
| 4{4}2, cu 16 vârfuri și 8 4-fețe, 4 dintre ele fiind colorate roșu și celelalte 4 albastru | |
Politopul complex regulat 4{4}2, ![]()
![]()
![]() , în are o reprezentare reală în spațiul 4-dimensional ca tesseract sau 4-4 duoprismă. 4{4}2 are 16 vârfuri și 8 4-laturi. Simetria sa este 4[4]2, ordinul 32. Are și o construcție cu o simetrie mai mică,
, în are o reprezentare reală în spațiul 4-dimensional ca tesseract sau 4-4 duoprismă. 4{4}2 are 16 vârfuri și 8 4-laturi. Simetria sa este 4[4]2, ordinul 32. Are și o construcție cu o simetrie mai mică, ![]()
![]()
![]() sau 4{}×4{}, cu simetrie 4[2]4, ordinul 16. Aceasta este simetria dacă 4-laturile roșii și albastre sunt considerate distincte.[10]
sau 4{}×4{}, cu simetrie 4[2]4, ordinul 16. Aceasta este simetria dacă 4-laturile roșii și albastre sunt considerate distincte.[10]
Politopuri și faguri asociați[modificare | modificare sursă]
Ca duoprismă uniformă, tesseractul există într-o secvență de duoprisme uniforme: {p}×{4}.
Tesseractul regulat împreună cu 16-celule, face parte dintr-un set de 15 4-politopuri uniforme cu aceeași simetrie. Tesseractul {4,3,3} face parte dintr-o secvență de 4-politopuri și faguri, {p,3,3} cu figurile vârfului tetraedre, {3,3}. De asemenea, tesseractul face parte din secvența de 4-politopuri și faguri regulați, {4,3,p} cu celule cubice.
În cultura populară[modificare | modificare sursă]
De la descoperirea lor, hipercuburile cu patru dimensiuni au fost o temă populară în artă, arhitectură și science fiction. Exemple notabile sunt:
- And He Built a Crooked House (română Și el construi o casă în dungă, o casă în dungă) de Robert Heinlein, o povestire științifico-fantastică din 1940, descrie o casă în formă de un hipercub în 4 dimensiuni.[11][12] Acesta, împreună cu Martin Gardner, care a publicat în 1946 povestirea "The No-Sided Professor", sunt printre primii din domeniul științifico-fantastic care au popularizat banda lui Möbius, sticla lui Klein și hipercubul (tesseractul).
- Crucifixión (română Răstignire), o pictură în ulei din 1954 de Salvador Dalí în care este reprezentată o desfășurată tridimensională a hipercubului 4-dimensional.[13]
- Grande Arche, un monument și o clădire lângă Paris, finalizată în 1989. Potrivit proiectantului monumentului, Erik Reitzel, Grande Arche a fost făcut să semene cu proiecția unui hipercub.[14]
- Cubul Cosmic, redenumit Tesseract, în Universul Cinematografic Marvel.[15]
Note[modificare | modificare sursă]
- ^ en „Unfolding an 8-cell”. Unfolding.apperceptual.com. Accesat în .
- ^ „The Tesseract - a 4-dimensional cube”. www.cut-the-knot.org. Accesat în .
- ^ en Matila Ghyka, The geometry of Art and Life (1977), p.68
- ^ en Elte, E. L. (). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
- ^ Coxeter 1973, pp. 122-123, §7.2. illustration Fig 7.2C.
- ^ en „Home : Oxford English Dictionary”. Oed.com. Arhivat din original la . Accesat în .
- ^ Coxeter 1973, p. 293.
- ^ en Pournin, Lionel (), „The flip-Graph of the 4-dimensional cube is connected”, Discrete & Computational Geometry, 49 (3): 511–530, arXiv:1201.6543
 , doi:10.1007/s00454-013-9488-y, MR 3038527
, doi:10.1007/s00454-013-9488-y, MR 3038527
- ^ en Cottle, Richard W. (), „Minimal triangulation of the 4-cube”, Discrete Mathematics, 40: 25–29, doi:10.1016/0012-365X(82)90185-6, MR 0676709
- ^ en Coxeter, H.S.M., Regular Complex Polytopes, Ed. a II-a, Cambridge University Press, 1991
- ^ Fowler, David (), „Mathematics in Science Fiction: Mathematics as Science Fiction”, World Literature Today, 84 (3): 48–52, JSTOR 27871086
- ^ en Henderson, Linda Dalrymple (noiembrie 2014), „Science Fiction, Art, and the Fourth Dimension”, În Emmer, Michele, Imagine Math 3: Between Culture and Mathematics, Springer International Publishing, pp. 69–84, doi:10.1007/978-3-319-01231-5_7
- ^ en Kemp, Martin (), „Dali's dimensions”, Nature, 391 (27): 27, Bibcode:1998Natur.391...27K, doi:10.1038/34063
- ^ en Ursyn, Anna (), „Knowledge Visualization and Visual Literacy in Science Education”, Knowledge Visualization and Visual Literacy in Science Education, Information Science Reference, p. 91, ISBN 9781522504818
- ^ Yamato, Jen (). „Kevin Feige on Avengers, Marvel Universe-Building, and the Legacy of Elektra”. Movieline.
Bibliografie[modificare | modificare sursă]
- en Coxeter, H.S.M. (). Regular Polytopes (ed. 3rd). New York: Dover. pp. 122–123.
- en F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) Kaleidoscopes: Selected Writings of H.S.M. Coxeter, Wiley-Interscience Publication ISBN: 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, Mathematische Zeitschrift 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008) The Symmetries of Things, ISBN: 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- en T. Gosset (1900) On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan.
- en T. Proctor Hall (1893) "The projection of fourfold figures on a three-flat", American Journal of Mathematics 15:179–89.
- en Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- de Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren.
Legături externe[modificare | modificare sursă]
- en Eric W. Weisstein, Tesseract la MathWorld.
- en Klitzing, Richard. „4D uniform polytopes (polychora) x4o3o3o - tes”.
- en The Tesseract Arhivat în , la Wayback Machine. Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
- de Marco Möller, Der 8-Zeller: Politopuri regulate în ℝ4
- en WikiChoron: Tesseract
- en HyperSolids is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
- en Hypercube 98 A Windows program that displays animated hypercubes, by Rudy Rucker
- en ken perlin's home page A way to visualize hypercubes, by Ken Perlin
- en Some Notes on the Fourth Dimension includes animated tutorials on several different aspects of the tesseract, by Davide P. Cervone
- en Tesseract animation with hidden volume elimination
| Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familie | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Poligoane regulate | Triunghi | Pătrat | p-gon | Hexagon | Pentagon | |||||||
| Poliedre uniforme | Tetraedru | Octaedru • Cub | Semicub | Dodecaedru • Icosaedru | ||||||||
| 4-politopuri uniforme | 5-celule | 16-celule • Tesseract | Semitesseract | 24-celule | 120-celule • 600-celule | |||||||
| 5-politopuri uniforme | 5-simplex | 5-ortoplex • 5-cub | 5-semicub | |||||||||
| 6-politopuri uniforme | 6-simplex | 6-ortoplex • 6-cub | 6-semicub | 122 • 221 | ||||||||
| 7-politopuri uniforme | 7-simplex | 7-ortoplex • 7-cub | 7-semicub | 132 • 231 • 321 | ||||||||
| 8-politopuri uniforme | 8-simplex | 8-ortoplex • 8-cub | 8-semicub | 142 • 241 • 421 | ||||||||
| 9-politopuri uniforme | 9-simplex | 9-ortoplex • 9-cub | 9-semicub | |||||||||
| 10-politopuri uniforme | 10-simplex | 10-ortoplex • 10-cub | 10-semicub | |||||||||
| n-politopuri uniforme | n-simplex | n-ortoplex • n-cub | n-semicub | 1k2 • 2k1 • k21 | n-politop pentagonal | |||||||
| Topicuri: Familii de politopuri • Politop regulat | ||||||||||||



