Spațiu tridimensional

| Geometrie |
|---|
 |
|
|
Cvadri- și n-dimensional |
Un spațiu tridimensional, spațiu cu trei dimensiuni sau 3-spațiu este un spațiu geometric în care sunt necesare trei valori (numite coordonate) pentru a determina poziția unui punct). Acesta este sensul informal al termenului dimensiune.
În fizică și matematică, o secvență de n numere reale poate fi considerată o locație într-un spațiu n-dimensional. Când n = 3, mulțimea tuturor acestor locații se numește spațiu euclidian tridimensional (sau pur și simplu spațiu euclidian când contextul este clar). Este reprezentat în mod obișnuit de simbolul ℝ3.[1][2] Acesta servește ca model cu trei coordonate al universului fizic (adică, partea spațială, fără a lua în considerare timpul), în care există toată materia cunoscută. Deși acest spațiu rămâne cel mai convingător și util mod de a modela lumea așa cum este percepută experimental,[3] este doar un exemplu din marea varietate de spații cu trei dimensiuni numite 3-varietăți. În acest exemplu clasic, atunci când cele trei valori se referă la măsurători în direcții diferite (coordonate), pot fi alese oricare trei direcții, cu condiția ca vectorii cu aceste direcții să nu fie toți în același 2-spațiu (plan). De obicei aceste trei valori sunt denumite lungime, lățime și înălțime, dar există și alte variante.
În geometria euclidiană[modificare | modificare sursă]
Sisteme de coordonate[modificare | modificare sursă]
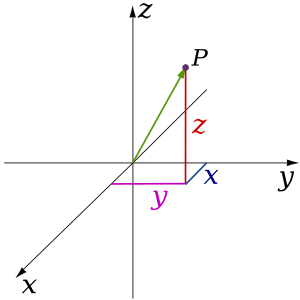
În matematică, geometria analitică (numită și „geometrie carteziană”) descrie fiecare punct din spațiul tridimensional prin intermediul a trei coordonate. Se dau trei axe de coordonate, fiecare perpendiculară pe celelalte două în origine, punctul în care se intersectează. De obicei sunt etichetate x, y și z. În raport cu aceste axe, poziția oricărui punct din spațiul tridimensional este dată de un triplet ordonat de numere reale, fiecare număr oferind distanța acelui punct de la origine, măsurată de-a lungul axei date, care este egală cu distanța acelui punct de planul determinat de celelalte două axe.[4]
Alte metode de descriere a localizării unui punct în spațiul tridimensional sunt sistemele de coordonate cilindrice și coordonate sferice, dar există un număr infinit de metode posibile. Mai jos sunt imagini cu sistemele menționate mai sus.
- Sisteme de coordonate
Drepte și planuri[modificare | modificare sursă]
Două puncte diferite determină întotdeauna o dreaptă. Trei puncte diferite sunt coliniare sau determină un plan unic. Pe de altă parte, patru puncte diferite pot fi fie coliniare, fie coplanare, fie pot determina întregul spațiu.
Două drepte diferite pot fi fie concurente, fie paralele, fie necoplanare. Două drepte paralele sau două drepte concurente se află într-un plan unic, deci dreptele necoplanare sunt drepte care nu se întâlnesc și nu se află într-un plan comun.
Două plane diferite se pot intersecta într-o dreaptă comună sau sunt paralele (adică nu se întâlnesc). Trei plane diferite, dintre care nici o pereche nu sunt paralele, se pot întâlni fie într-o dreaptă comună, fie într-un punct comun unic, fie nu au niciun punct comun toate trei. În ultimul caz, cele trei drepte de intersecție ale fiecărei perechi de plane sunt reciproc paralele.
O dreaptă poate fi situată într-un plan dat, poate intersecta acel plan într-un punct unic sau poate fi paralelă cu planul. În ultimul caz, vor exista drepte în plan care sunt paralele cu dreapta dată.
Un hiperplan este un subspațiu cu o dimensiune mai mică decât dimensiunea spațiului complet. Hiperplanele unui spațiu tridimensional sunt subspații bidimensionale, adică plane. În ceea ce privește coordonatele carteziene, punctele unui hiperplan satisfac o singură ecuație liniară, deci planele din acest 3-spațiu sunt descrise prin ecuații liniare. O dreaptă poate fi descrisă de o pereche de ecuații liniare independente — fiecare reprezentând un plan având această dreaptă drept intersecția lor.
Teorema Varignon afirmă că punctele din mijlocul laturilor oricărui patrulater din ℝ3 formează un paralelogram și, prin urmare, sunt coplanare.
Sfere și bile[modificare | modificare sursă]

O sferă în 3-spațiu (numită și 2-sferă deoarece este un obiect bidimensional) constă din mulțimea tuturor punctelor din 3-spațiu la o distanță fixă, r, de un punct central P. Interiorul sferei se numește bilă (sau, aici mai exact, o 3-bilă). Volumul bilei este dat de:
- .
Un alt tip de sferă apare dintr-o 4-bilă, a cărei suprafață tridimensională este o 3-sferă: puncte echidistante de originea spațiului euclidian ℝ4. Dacă un punct are coordonatele P(x,y,z,w), atunci caracterizează punctele de pe 3-sfera unitate (centrată în origine).
Politopuri[modificare | modificare sursă]
În trei dimensiuni există nouă politopuri regulate: cele cinci poliedre platonice și cele patru stelate, poliedrele Kepler–Poinsot.
| Clasa | Poliedre platonice | Poliedre Kepler–Poinsot | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Simetrie | Td | Oh | Ih | ||||||
| Grup Coxeter | A3, [3,3] | B3, [4,3] | H3, [5,3] | ||||||
| Ordin | 24 | 48 | 120 | ||||||
| Poliedru regulat |
{3,3} |
 {4,3} |
 {3,4} |
 {5,3} |
{3,5} |
 {5/2,5} |
 {5,5/2} |
{5/2,3} |
 {3,5/2} |
Suprafețe de revoluție[modificare | modificare sursă]
O suprafață generată prin rotirea unei curbe plane în jurul unei drepte fixe în planul său ca axă se numește suprafața de revoluție. Curba plană se numește generatoarea suprafeței. O secțiune a suprafeței, realizată prin intersecția suprafeței cu un plan perpendicular (ortogonal) pe axă, este un cerc.
Exemple simple se obțin atunci când generatoarea este o dreaptă. Dacă dreapta generatoare intersectează axa, suprafața de revoluție este un con cu vârful (apexul) în punctul de intersecție. Dacă generatoarea și axa sunt paralele, atunci suprafața de revoluție este un cilindru.
Cuadrice[modificare | modificare sursă]
Analog cu conicele, ansamblul de puncte ale căror coordonate carteziene satisfac ecuația generală de gradul al doilea, și anume,
unde A, B, C, F, G, H, J, K, L și M sunt numere reale și nu toate dintre A, B, C, F, G și H sunt zero, se numesște cuadrică.[5]
Există șase tipuri de cuarice nedegenerate:
- Elipsoidul
- Hiperboloidul cu o pânză
- Hiperboloidul cu două pânze
- Conul eliptic
- Paraboloidul eliptic
- Paraboloidul hiperbolic
Cuadricele degenerate pot fi mulțimea vidă, un singur punct, o singură dreaptă, un singur plan, o pereche de plane sau un cilindru pătratic (o suprafață constând dintr-o secțiune conică nedegenerată într-un plan și toate dreptele din ℝ3 prin acea conică care sunt normale pe [5] Conurile eliptice sunt uneori considerate și ele a fi cuadrice degenerate.
Hiperboloidul cu o pânză este o suprafață riglată, ceea ce înseamnă că poate fi generat de o familie de drepte. De fapt, are două familii de drepte generatoare, membrii fiecărei familii sunt disjuncti și fiecare membru intersectează, cu o singură excepție, fiecare membru al celeilalte familii.[6]
În algebra liniară[modificare | modificare sursă]
Un alt punct de vedere cu privire la spațiul tridimensional se găsește în algebra liniară, unde ideea de independență este esențială. Spațiul are trei dimensiuni deoarece lungimea unui paralelipiped dreptunghic este independentă de lățimea sau înălțimea sa. În limbajul algebrei liniare spațiul este tridimensional deoarece fiecare punct din spațiu poate fi descris printr-o combinație liniară de trei valori (vector cu trei componente).
Produs scalar, unghi și lungime[modificare | modificare sursă]
Un vector poate fi reprezentat ca o săgeată. Modulul vectorului este lungimea sa, iar direcția sa este direcția indicată de săgeată. Un vector din ℝ3 poate fi reprezentat printr-un triplet ordonat de numere reale. Aceste numere sunt denumite „componentele” vectorului.
Produsul scalar al doi vectori și este definit drept:[7]
Modulul vectorului este notat cu . Produsul scalar al vectorului cu el însuși este:
adică
care este formula lungimii euclidiene a vectorului.
Fără a se referi la componentele vectorilor, produsul scalar al a doi vectori euclidieni diferiți de zero și este dat de:[8]
unde θ este unghiul dintre A și B.
Produs vectorial[modificare | modificare sursă]
Produsul vectorial al doi vectori și este un vector în spațiul tridimensional. Operația este notată prin simbolul ×. Produsul este perpendicular pe ambii și , adică este normal pe planul care-i conține pe ambii. Are multe aplicații în matematică, fizică și inginerie.
Spațiul și produsul formează o algebră peste un corp, care nu este nici comutativ, nici asociativ, dar este o algebră Lie, produsul vectorial fiind o paranteză Lie.
Într-un n-spațiu se poate folosi produsul a n – 1 vectori pentru a genera un vector perpendicular pe toți. Dar dacă produsul este limitat la produse binare nebanale cu rezultate vectoriale, acesta există doar în trei și șapte dimensiuni.[9]

În calcule[modificare | modificare sursă]
Gradient, divergență și rotor[modificare | modificare sursă]
Într-un sistem de coordonate rectangular, gradientul este dat de:
Divergența unui câmp vectorial continuu derivabil F = U i + V j + W k este egală cu funcția scalară:
Dezvoltat în coordonate carteziene, rotorul ∇ × F este, pentru F compus din [Fx, Fy, Fz]:
unde i, j, and k sunt versorii pe axele x, y, respectiv z. Dezvoltarea este:[10]
Integrale, integrale de suprafață și integrale de volum[modificare | modificare sursă]
Pentru un câmp scalar f : U ⊆ Rn → R, integrala curbei continue C ⊂ U este definită drept
unde r: [a, b] → C este o parametrizare bijectivă a curbei C astfel încât r(a) și r(b) să fie capetele lui C iar .
Pentru un câmp vectorial F : U ⊆ Rn → Rn, integrala curbei continue C ⊂ U în direcția lui r este definită drept
unde · este produsul scalar iar r: [a, b] → C este o parametrizare bijectivă a curbei C astfel încât r(a) și r(b) să fie capetele lui C.
O integrală de suprafață este o generalizare a integralei multiple la integrarea pe Suprafață. Se poate considera că este analoaga integralei duble. Pentru a găsi o formulă explicită pentru integrala de suprafață, trebuie parametrizată suprafața S, luând în considerare un sistem de coordonate curbilinii pe S, ca latitudine și longitudine pe o sferă. Fie o astfel de parametrizare x (s, t), unde (s, t) variază în anumite regiuni T din plan. Apoi, integrala de suprafață este dată de:
unde expresia dintre bare din partea dreaptă este magnitudinea produsului vectorial al derivatelor parțiale x(s,t) și este cunoscută sub numele de suprafața elementului. Fiind dat un câmp vectorial v pe S, aceasta este o funcție care atribuie fiecărui x din S un vector v(x), integrala de suprafață poate fi definită în funcție de componente conform definiției integralei de suprafață a unui câmp scalar; rezultatul este un vector.
O integrală de volum este o integrală pe un domeniu tridimensional. Poate însemna și o integrală triplă într-o regiune D din R3 a funcției și este exprimată prin:
Teorema gradientului[modificare | modificare sursă]
Teorema gradientului afirmă că integrala unui gradient poate fi calculată din valorile câmpului scalar original la capetele curbei. Fie . Atunci:
Teorema Kelvin–Stokes[modificare | modificare sursă]
Teorema Kelvin–Stokes leagă integrala de suprafață a rotorului unui câmp vectorial F pe suprafața euclidiană tridimensională Σ de integrala câmpului vectorial pe frontiera sa, ∂Σ:
Teorema divergenței[modificare | modificare sursă]
Presupunând că V este o submulțime a (în cazul reprezintă un volume în 3-spațiu) care este compactă și are frontiera netedă pe porțiuni S (notată și . Dacă F este un câmp vectorial continuu derivabil definit în vecinătatea lui V, atunci teorema divergenței afirmă că:[11]
Partea stângă este integrala de volum pe volumul V, partea dreaptă este integrala de suprafață pe limita volumului V. Varietatea închisă ∂V este, în general, frontiera lui V ca suprafață normală orientată spre exterior, iar n este câmpul unitate normal orientat spre exteriorul frontierei ∂V. (notația dS poate fi folosită ca o prescurtare pentru ndS .)
În topologie[modificare | modificare sursă]

Spațiul tridimensional are o serie de proprietăți topologice care îl disting de spațiile cu alte numere de dimensiuni. De exemplu, sunt necesare cel puțin trei dimensiuni pentru a face un nod într-o bucată de sfoară.[12]
În geometria diferențială spațiile tridimensionale generice sunt 3-varietăți, care seamănă local cu .
În geometria finită[modificare | modificare sursă]
Multe idei cu privire la dimensiuni pot fi testate în geometria finită. Cea mai simplă formă este PG (3,2), care are plane Fano ca subspații bidimensionale. Este o formă din geometria Galois, un studiu al geometriei proiective folosind câmpuri finite. Astfel, pentru orice câmp Galois GF(q), există un spațiu proiectiv PG(3,q) cu trei dimensiuni. De exemplu, oricare trei drepte neconcurente din PG(3,q) sunt conținute în exact un regulus.[13]
Note[modificare | modificare sursă]
- ^ en „Compendium of Mathematical Symbols”. Math Vault (în engleză). . Accesat în .
- ^ en „Euclidean space - Encyclopedia of Mathematics”. encyclopediaofmath.org. Accesat în .
- ^ „Euclidean space | geometry”. Encyclopedia Britannica (în engleză). Accesat în .
- ^ en Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (). Calculus : Single and Multivariable (ed. 6). John wiley. ISBN 978-0470-88861-2.
- ^ a b Brannan, Esplen & Gray 1999, pp. 34–5.
- ^ Brannan, Esplen & Gray 1999, pp. 41–2.
- ^ Anton 1994, p. 133.
- ^ Anton 1994, p. 131.
- ^ en WS Massey (). „Cross products of vectors in higher dimensional Euclidean spaces”. The American Mathematical Monthly. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537.
If one requires only three basic properties of the cross product ... it turns out that a cross product of vectors exists only in 3-dimensional and 7-dimensional Euclidean space.
- ^ Arfken, p. 43
- ^ en M. R. Spiegel; S. Lipschutz; D. Spellman (). Vector Analysis. Schaum’s Outlines (ed. 2nd). USA: McGraw Hill. ISBN 978-0-07-161545-7.
- ^ en Rolfsen, Dale (). Knots and Links. Berkeley, California: Publish or Perish. ISBN 0-914098-16-0.
- ^ Albrecht Beutelspacher, Ute Rosenbaum (1998). Projective Geometry, p. 72, Cambridge University Press ISBN: 0-521-48277-1
Bibliografie[modificare | modificare sursă]
- en Anton, Howard (), Elementary Linear Algebra (ed. 7th), John Wiley & Sons, ISBN 978-0-471-58742-2
- en George B. Arfken, Hans J. Weber, Mathematical Methods For Physicists, Academic Press; 6 edition (June 21, 2005). ISBN: 978-0-12-059876-2.
- en Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (), Geometry, Cambridge University Press, ISBN 978-0-521-59787-6
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
 Materiale media legate de Spațiu tridimensional la Wikimedia Commons
Materiale media legate de Spațiu tridimensional la Wikimedia Commons- en Eric W. Weisstein, Four-Dimensional Geometry la MathWorld.
- en Elementary Linear Algebra - Chapter 8: Three-dimensional Geometry Keith Matthews de la University of Queensland, 1991





























![{\displaystyle \varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p} ,\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b27cdd0377931a70cbb0635e37781a42e7fe33f9)








