Cuadrică

În matematică, cuadricele sunt suprafețe algebrice de gradul al doilea, adică suprafețe ale spațiului afin euclidian tridimensional, a căror ecuație se obține prin anularea unui polinom de gradul al doilea în trei variabile.[1]
Prin generalizare, se poate vorbi de suprafețe n-dimensionale în spațiul cu n + 1 dimensiuni generate de locul geometric al soluțiilor unui polinom de gradul doi. În coordonate {x1, x2, ..., xn+1}, cuadrica generată este definită de o ecuație algebrică de forma:[2]
care poate fi scrisă compact în notație matricială:
unde x = {x1, x2, ..., xn+1} este o matrice vector linie, xT este transpusa lui x (un vector coloană), Q este o matrice (n + 1)×(n + 1), P este un vector linie (n + 1)-dimensional, iar R este o constantă scalară. Valorile din Q, P și R sunt de obicei numere reale sau complexe, dar de fapt o cuadrică poate fi definită pe orice inel. În general, locurile geometrice ale soluțiilor polinoamelor sunt varietăți algebrice și fac obiectul geometriei algebrice.
Planul și spațiul euclidian
[modificare | modificare sursă]În planul euclidian cuadricele au o singură dimensiune (n = 1), adică sunt linii, curbe. Aceste cuadrice sunt identice cu secțiunile conice și sunt cunoscute sub numele de conice.

În spațiul euclidian cuadricele au două dimensiuni (n = 2), și formează suprafețe cuadice. Printr-o schimbare de variabilă potrivită (transformare izometrică) și alegerea direcțiilor axelor orice cuadrică din spațiul euclidian poate fi adusă la forma canonică.[3] În spațiul euclidian tridimensional există 16 asemenea forme. Dintre acestea, 11 sunt degenerate. Formele degenerate conțin planuri, linii, puncte sau chiar nimic din acestea.[4]
| Cuadrice nedegenerate | ||
|---|---|---|
| Elipsoid[5] | 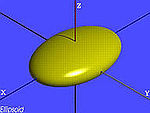
| |
| Sferoid (caz particular al elipsoidului) | ||
| Sferă (caz particular al sferoidului) | ||
| Paraboloid eliptic[6] | 
| |
| Paraboloid de rotație (caz particular al paraboloidului eliptic) | ||
| Paraboloid hiperbolic[7] | 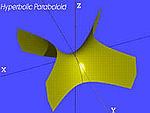
| |
| Hiperboloid cu o pânză[5] | 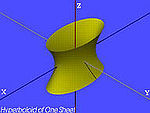
| |
| Hiperboloid cu două pânze[6] | 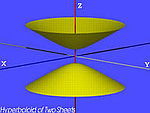
| |
| Cuadrice degenerate | ||
| Con[7] | 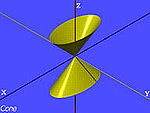
| |
| Con de rotație (caz particular al conului) | ||
| Cilindru eliptic[8] | 
| |
| Cilindru de rotație (caz particular al cilindrului eliptic) | ||
| Cilindru hiperbolic[8] | 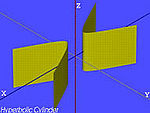
| |
| Cilindru parabolic[9] | 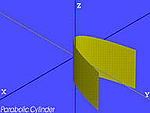
| |
Note
[modificare | modificare sursă]- ^ Brăescu, p. 50
- ^ en Quadrics Arhivat în , la Wayback Machine. în Geometry Formulas and Facts de Silvio Levy, extras din cea de a 30-a ediție a CRC Standard Mathematical Tables and Formulae (CRC Press).
- ^ Emil Stoica, Cap 9 (Cuadrice)[nefuncțională], p. 187, Universitatea Transilvania din Brașov, accesat 2011-02-04
- ^ en Stewart Venit and Wayne Bishop, Elementary Linear Algebra (fourth edition), International Thompson Publishing, 1996.
- ^ a b Brăescu, p. 51
- ^ a b Brăescu, p. 52
- ^ a b Brăescu, p. 53
- ^ a b Brăescu, p. 54
- ^ Brăescu, p. 55
Bibliografie
[modificare | modificare sursă]- Liliana Brăescu, Eva Kaslik, Simina Mariș, Simona Epure, Ioan Rodilă, Curs de geometrie Arhivat în , la Wayback Machine., Universitatea de Vest din Timișoara, Facultatea de Matematică și Informatică, Departamentul de Informatică
















