Degenerare (matematică)
În matematică un caz degenerat este un caz limită al unei clase de obiecte care pare a fi diferit calitativ de (și de obicei mai simplu decât) restul clasei,[1] iar termenul degenerare este condiția de a fi un caz degenerat.[2]
Definițiile multor clase de obiecte compuse sau structurate includ adesea implicit inegalități. De exemplu, unghiurile și lungimile laturilor unui triunghi se presupune că sunt pozitive. Cazurile limită, în care una sau mai multe dintre aceste inegalități devin egalități, sunt degenerări. În cazul triunghiurilor, un triunghi este „degenerat” dacă cel puțin o lungime a unei laturi sau unghi este zero, caz în care devine de fapt un segment.[3]
Adesea cazurile degenerate sunt cazurile excepționale în care apar modificări ale dimensiunii obișnuite sau la cardinalitatea obiectului (sau a unei părți a acestuia). De exemplu, un triunghi este un obiect bidimensional, iar un triunghi degenerat este conținut într-o dreaptă unidimensională.[3] Un caz similar este un cerc cu raza 0, care degenerează într-un punct zerodimensional.[1]
Alt exemplu este mulțimea soluțiilor unui sistem de ecuații care depinde de un parametru are în general o anume cardinalitate și dimensiune, dar cardinalitatea și/sau dimensiunea pot fi diferite pentru unele valori excepționale, numite cazuri degenerate. Într-un astfel de caz degenerat se spune că acele soluții sunt degenerate.
Pentru unele clase de obiecte compozite, cazurile degenerate depind de proprietățile care sunt studiate expres. În special, clasa de obiecte poate fi adesea definită sau caracterizată prin sisteme de ecuații. În majoritatea scenariilor, o anumită clasă de obiecte poate fi definită de mai multe sisteme diferite de ecuații, iar aceste sisteme diferite de ecuații pot duce la cazuri degenerate diferite, caracterizând în același timp aceleași cazuri nedegenerate. Acesta poate fi motivul pentru care nu există o definiție generală a degenerării, în ciuda faptului că conceptul este utilizat pe scară largă și definit (dacă este necesar) în fiecare situație specifică.
Un caz degenerat are astfel caracteristici speciale care îl fac să nu fie generic. Totuși, nu toate cazurile care nu sunt generice sunt degenerate. De exemplu, triunghiurile dreptunghice, isoscele și echilaterale nu sunt generice, dar nici degenerate. De fapt, cazurile degenerate corespund adesea singularităților, fie prin obiect, fie prin spațiul de configurație(d). De exemplu, o conică este degenerată dacă și numai dacă are puncte singulare (de exemplu punct, linie, linii de intersectare[4]).
În geometrie[modificare | modificare sursă]
Secțiuni conice[modificare | modificare sursă]
O conică degenerată este o conică (o curbă plană de gradul doi, definită printr-o ecuație polinomială de gradul al doilea) care însă nu este o curbă ireductibilă.
- Un punct este un cerc degenerat, și anume unul cu raza 0.[1]
- dreapta este un caz degenerat al unei parabole dacă parabola se află pe un plan tangent. Uneori o dreaptă este considerată un caz degenerat al unui cerc cu rază infinită.
- Două drepte paralele formează, de asemenea, o parabolă degenerată.
- Un segment poate fi privit ca un caz degenerat al unei elipse în care semiaxa mică este zero, focarele se află la capetele segmentului, iar excentricitatea este 1.
- Un cerc poate fi considerat ca o elipsă degenerată, pe măsură ce excentricitatea se apropie de 0 și focarele se suprapun.[1]
- O elipsă poate degenera și într-un singur punct.
- O hiperbolă poate degenera în două drepte care se intersectează într-un punct, o familie de hiperbole având acele drepte drept asimptote comune.
Triunghi[modificare | modificare sursă]
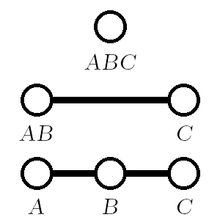
- Un triunghi degenerat are vârfurile coliniare[3] și aria zero, astfel coincide cu un segment acoperit de două ori (dacă cele trei vârfuri nu sunt toate suprapuse, caz în care triunghiul degenerează într-un singur punct). Dacă cele trei vârfuri sunt distincte în perechi, acesta are două unghiuri de 0° și un unghi de 180°. Dacă două vârfuri sunt suprapuse, are un unghi de 0° și două unghiuri nedefinite.
Dreptunghi[modificare | modificare sursă]
- Un segment este un caz degenerat al unui dreptunghi care are o latură de lungime 0.
- Pentru orice submulțime nevidă , există un dreptunghi degenerat mărginit, aliniat pe axe și ai, bi, ci sunt constante (cu ai ≤ bi pentru orice i). Numărul de laturi degenerate ale lui R este numărul de elemente ale submulțimii S. Astfel, poate exista doar o „parte” degenerată sau toate n (caz în care R se reduce la un punct singleton).
Poligon convex[modificare | modificare sursă]
- Un poligon convex este degenerat dacă cel puțin două laturi consecutive coincid cel puțin parțial, sau cel puțin o latură are lungimea zero, sau cel puțin un unghi este de 180°. Astfel, un poligon convex degenerat cu n laturi arată ca un poligon cu mai puține laturi. În cazul triunghiurilor, această definiție coincide cu cea dată mai sus.
Poliedru convex[modificare | modificare sursă]
- Un poliedru convex este degenerat dacă fie două fațete adiacente sunt coplanare, fie două muchii sunt aliniate. În cazul unui tetraedru, acest lucru este echivalent cu a spune că toate vârfurile se află în același plan, ca urmare volumul său este 0.
Tor[modificare | modificare sursă]
- În contextele în care autointersecția este permisă, o sferă este un tor degenerat în care axa de revoluție trece prin centrul cercului generator.
- Un tor degenerează într-un cerc când raza lui minoră este 0.
Sferă[modificare | modificare sursă]
- Când raza unei sfere este 0, sfera degenerată rezultată cu volum zero este un punct.
Alte cazuri[modificare | modificare sursă]
- O mulțime care conține un singur punct este un continuum degenerat.
- Obiecte precum digonul și monogonul pot fi privite drept cazuri degenerate de poligoane: valabile într-un sens matematic abstract general, dar nu fac parte din concepția originală euclidiană a poligoanelor.
- O variabilă aleatoare care poate lua o singură valoare are o distribuție degenerată; dacă acea valoare este numărul real 0, atunci densitatea sa de probabilitate este funcția lui Dirac.
- Rădăcinile unui polinom se spune că sunt degenerate dacă coincid, deoarece în mod generic cele n rădăcini ale unui polinom de gradul n sunt toate distincte.[1] Această utilizare se transferă la problemele proprii: o valoare proprie degenerată (adică o rădăcină coincidentă multiplă a polinomului caracteristic) este una care are mai mulți vectori proprii liniar independent.
- În mecanica cuantică, orice astfel de multiplicitate în valorile proprii ale hamiltonianului dă naștere la niveluri de energie degenerate. De obicei, orice astfel de degenerare indică o simetrie de bază în sistem.
Note[modificare | modificare sursă]
- ^ a b c d e en Weisstein, Eric W. „Degenerate”. mathworld.wolfram.com (în engleză). Accesat în .
- ^ en „Definition of DEGENERACY”. www.merriam-webster.com. Accesat în .
- ^ a b c en „Mathwords: Degenerate”. www.mathwords.com. Accesat în .
- ^ en „Mathwords: Degenerate Conic Sections”. www.mathwords.com. Accesat în .


