Interior (topologie)

În matematică, În matematică, în special în topologie, interiorul unei submulțimi $S$ a unui spațiu topologic $X$ este reuniunea tuturor submulțimilor lui $S$ care sunt deschise în $X$ . Un punct care se află în interiorul lui $S$ este un punct interior al lui $S$ .

Interiorul lui $S$ este complementul (absolut) al închiderii complementului lui $S$ . În acest sens interiorul și închiderea sunt noțiuni duale.

Exteriorul unei mulțimi $S$ este complementul închiderii lui $S$ ; el este format din punctele care nu sunt în $S$ , nici în interiorul său, nici pe frontiera sa.

Interiorul, frontiera și exteriorul unei submulțimi împart împreună întregul spațiu în trei zone (sau mai puțin atunci când una sau mai multe dintre acestea sunt vide). Interiorul și exteriorul sunt întotdeauna deschise, în timp ce frobtiera este întotdeauna închisă. Mulțimile cu interior vid au fost numite mulțimi de frontieră.^[1]

Definiții[modificare | modificare sursă]

Punct din interior[modificare | modificare sursă]

Dacă $S$ este o submulțime a unui spațiu euclidian, atunci $x$ este un punct interior al lui $S$ dacă există o bilă deschisă cu centrul în $x$ care este complet inclusă în $S$ . (Acest lucru este ilustrat în imaginea din introducerea acestui articol.)

Această definiție se generalizează la orice submulțime $S$ a unui spațiu metric $X$ cu metrică $d$ : $x$ este un punct interior al lui $S$ dacă există $r>0\,$ astfel încât $y$ este inclus în $S$ ori de câte ori distanța $d (x, y) < r$ .

Această definiție se generalizează în spațiile topologice prin înlocuirea „bilei deschise” cu „mulțime deschisă”. Fie $S$ o submulțime a unui spațiu topologic $X$ . Atunci $x$ este un punct interior al lui $S$ dacă $x$ este inclus într-o submulțime deschisă a lui $X$ care este complet inclus în $S$ . (În mod echivalent, $x$ este un punct interior al lui $S$ dacă $S$ este o vecinătate a lui $x$ .)

Interiorul unei mulțimi[modificare | modificare sursă]

Interiorul unei submulțimi $S$ a unui spațiu topologic $X$ , notat cu $Int S$ sau cu $S °$ poate fi definit în oricare dintre următoarele moduri echivalente:

$Int S$ este cea mai mare submulțime deschisă a $X$ inclusă (ca submulțime) în $S$ ;
$Int S$ este reuniunea tuturor mulțimilor deschise din $X$ incluse în $S$ ;
$Int S$ este mulțimea tuturor punctelor din interiorul lui $S$ .

Exemple[modificare | modificare sursă]

a

este un punct din interiorul lui

M

deoarece există o ε-vecinătate care este o submulțime a

M

.

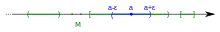
În orice spațiu, interiorul mulțimii vide este mulțimea vidă.
În orice spațiu $X$ , facă $S \subseteq X$ , atunci $int S \subseteq S$ .
Dacă $X$ este spațiul euclidian $ℝ$ al numerelor reale, atunci $int([0, 1]) = (0, 1)$ .
Dacă $X$ este spațiul euclidian $ℝ$ , atunci interiorul mulțimii $ℚ$ al numerelor raționale este vid.
Dacă $X$ este planul complex $\mathbb {C} =\mathbb {R} ^{2}$ , atunci $\operatorname {int} (\{z\in \mathbb {C} :|z|\leq 1\})=\{z\in \mathbb {C} :|z|<1\}.$
În orice spațiu euclidian interiorul oricărei mulțimi finite este mulțimea vidă.

Pe mulțimea numerelor reale se pot pune mai degrabă alte topologii decât cea standard.

Dacă $X = ℝ$ , unde $ℝ$ are topologie Sorgenfrey^⁠(d), atunci int([0, 1]) = [0, 1).
Dacă se consideră pe $ℝ$ topologia în care fiecare mulțime este una deschisă, atunci $int([0, 1]) = [0, 1]$ .
Dacă se consideră pe $ℝ$ topologia în care fiecare mulțime este una vidă, inclusiv $ℝ$ însăși, atunci $int([0, 1])$ este mulțimea vidă.

Aceste exemple arată că interiorul unei mulțimi depinde de topologia spațiului subiacent. Ultimele două exemple sunt cazuri particulare ale următoarelor.

În orice spațiu discret, deoarece fiecare mulțime este deschisă, fiecare mulțime este egală cu interiorul său.
În orice spațiu nediscret $X$ , deoarece singurele mulțimi deschise sunt mulțimea vidă și $X$ însăși, avem $X = int X$ și pentru orice submulțime proprie $S$ a lui $X$ , $int S$ este mulțimea vidă.

Proprietăți[modificare | modificare sursă]

Fie $X$ un spațiu topologic și $S$ și $T$ submulțimi ale lui $X$ .

$Int S$ este deschis în $X$ .
Dacă $T$ este deschisă în $X$ atunci $T \subseteq S$ dacă și numai dacă $T \subseteq Int S$ .
$Int S$ este o submulțime deschisă a $S$ când $S$ este dată de topologia de subspațiu.
$S$ este o submulțime deschisă a $X$ dacă și numai dacă $S = int S$ .
Intensivă: $Int S \subseteq S$ .
Idempotentă: $Int(Int S) = Int S$ .
Conservă distributivitatea intersecției binare: $Int (S \cap T) = (Int S) \cap (Int T)$ .
Monotonă / nedescrescătoare în raport cu $\subseteq$ : Dacă $S \subseteq T$ atunci $Int S \subseteq Int T$ .

Afirmațiile de mai sus vor rămâne adevărate dacă toate aparițiile simbolurilor / cuvintelor

"interior", "Int", "deschisă", "submulțime" și "cea mai mare"

sunt înlocuite respectiv cu

"închidere", "Cl", "închisă", "supermulțime" și "cea mai mică"

Iar următoarele simboluri sunt întoarse:

"⊆" devine "⊇"
"∪" devine "∩"

Alte proprietăți:

Dacă $S$ este închisă în $X$ și $Int T = \emptyset$ atunci $Int (S \cup T) = Int S$ .^[2]

Operatorul „interior”[modificare | modificare sursă]

Operatorul „interior”' ^o este dualul operatorului „închidere” ^—, în sensul că

S^{\circ }=X\backslash {\overline {(X\backslash S)}}

,

și

{\bar {S}}=X\backslash (X\backslash S)^{\circ }

,

unde $X$ este spațiul topologic care include $S$ , iar bara oblică inversă se referă la complementul relativ (diferența lor).

Prin urmare, teoria abstractă a operatorilor de închidere și axiomele de închidere Kuratowski pot fi ușor transpuse în limbjul operatorilor „interior”, prin înlocuirea mulțimilor cu complementele lor.

În general operatorul „interior” nu este comutativ pe reuniuni. Totuși, într-un spațiu metric complet următorul rezultat este valabil:^[3]

Fie

X

un spațiu metric complet și fie

S_{1},S_{2},\ldots

in șir de submulțimi ale

X

.

Dacă orice $S i$ este închisă în $X$ atunci $\operatorname {cl} \left(\bigcup _{i\in \mathbb {N} }\operatorname {int} S_{i}\right)=\operatorname {cl} \operatorname {int} \left(\bigcup _{i\in \mathbb {N} }S_{i}\right)$ .
Dacă orice $S i$ este deschisă în $X$ atunci $\operatorname {int} \left(\bigcap _{i\in \mathbb {N} }\operatorname {cl} S_{i}\right)=\operatorname {int} \operatorname {cl} \left(\bigcap _{i\in \mathbb {N} }S_{i}\right)$ .

Forme interior-disjuncte[modificare | modificare sursă]

Formele roșii nu sunt interior-disjuncte de triunghiul albastru; cele verzi și galbene sunt interior-disjuncte de triunghiul albastru, dar numai cea galbenă este complet disjunctă de triunghiul albastru

Două forme $a$ și $b$ se spune că sunt interior-disjuncte dacă intersecția interioarelor lor este vidă. Formele interior-disjuncte se pot intersecta sau nu pe frontierele lor.

Exteriorul unei mulțimi[modificare | modificare sursă]

Exteriorul unei submulțimi $S$ a unui spațiu topologic $X$ , notat $ext S$ sau $Ext S$ este interiorul $int(X \ S)$ complementului său relativ. Alternativ, poate fi definit ca $X \ S—$ , complementul închiderii lui $S$ . Multe proprietăți rezultă direct din cele ale operatorului „interior”, cum ar fi următoarele.

$ext S$ este o mulțime deschisă disjunctă de $S$ .
$ext S$ este reuniunea tuturor mulțimilor deschise disjuncte de $S$ .
$ext S$ este cea mai mare mulțime deschisă disjunctă de $S$ .
Dacă $S \subseteq T$ , atunci $ext(S)$ este o supermulțime a $ext T$ .

Diferit de operatorul „interior”, operatorul „exterior” nu este idempotent, dar este valabilă afirmația:

$ext(ext S)$ este o supermulțime a $int S$ .

Note[modificare | modificare sursă]

^ en Kuratowski, Kazimierz (1922). „Sur l'Operation Ā de l'Analysis Situs” (PDF). Fundamenta Mathematicae. Warsaw: Polish Academy of Sciences. 3: 182–199. ISSN 0016-2736.
^ Narici & Beckenstein 2011, pp. 371-423.
^ en Zalinescu, C (2002). Convex analysis in general vector spaces. River Edge, N.J. London: World Scientific. p. 33. ISBN 981-238-067-1. OCLC 285163112.

Bibliografie[modificare | modificare sursă]

en Bourbaki, Nicolas (1989) [1966]. General Topology: Chapters 1–4 [Topologie Générale]. Éléments de mathématique. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC 18588129.
en Dixmier, Jacques (1984). General Topology. Undergraduate Texts in Mathematics. Translated by Berberian, S. K. New York: Springer-Verlag. ISBN 978-0-387-90972-1. OCLC 10277303.
en Császár, Ákos (1978). General topology. Translated by Császár, Klára. Bristol England: Adam Hilger Ltd. ISBN 0-85274-275-4. OCLC 4146011.
en Dugundji, James (1966). Topology. Boston: Allyn and Bacon. ISBN 978-0-697-06889-7. OCLC 395340485.
en Joshi, K. D. (1983). Introduction to General Topology. New York: John Wiley and Sons Ltd. ISBN 978-0-85226-444-7. OCLC 9218750.
en Kelley, John L. (1975). General Topology. Graduate Texts in Mathematics. 27. New York: Springer Science & Business Media. ISBN 978-0-387-90125-1. OCLC 338047.
en Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
en Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
en Schubert, Horst (1968). Topology. London: Macdonald & Co. ISBN 978-0-356-02077-8. OCLC 463753.
en Willard, Stephen (2004) [1970]. General Topology. Dover Books on Mathematics (First ed.). Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.

Legături externe[modificare | modificare sursă]

Portal Matematică

Interior la PlanetMath

[1] Kuratowski, Kazimierz (1922). „Sur l'Operation Ā de l'Analysis Situs” (PDF). Fundamenta Mathematicae. Warsaw: Polish Academy of Sciences. 3: 182–199. ISSN 0016-2736.

[FOOTNOTENariciBeckenstein2011371-423-2] Narici & Beckenstein 2011, pp. 371-423.

[Zalinescu_2002_p._33-3] Zalinescu, C (2002). Convex analysis in general vector spaces. River Edge, N.J. London: World Scientific. p. 33. ISBN 981-238-067-1. OCLC 285163112.

[1]

[2]

[3]