Arc de cerc
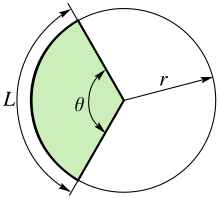
Un arc de cerc[1] este un arc al unui cerc dintre o pereche de puncte distincte. Dacă cele două puncte nu sunt direct opuse unul altuia, unul dintre aceste arcuri, arcul mic,[2] va subîntinde un unghi la centru care este mai mic de π radiani (180°), iar celălalt arc, arcul mare,[2] va subîntinde un unghi mai mare de π radiani.
Lungime
[modificare | modificare sursă]Lungimea unui arc de cerc cu raza "r" și care subîntinde un unghi la centru θ (măsurat în radiani) este: [3]
Asta deoarece
Substituind circumferința și simplificând se obține relația susmenționată:
Dacă α este același unghi, dar măsurat în grade, deoarece θ = α180π, lungimea arcului este
O modalitate practică de a determina lungimea unui arc de cerc este să se traseze două drepte din punctele finale ale arcului până la centrul cercului, să se măsoare unghiul dintre aceste drepte și apoi să se calculeze
- măsura unghiului în grade / 360° = L / circumferință.
De exemplu, dacă măsura unghiului este de 60° iar circumferința este de 24 m, atunci
Asta deoarece circumferința unui cerc și gradele unui cerc, care sunt întotdeauna 360, sunt direct proporționale.
Jumătatea superioară a unui cerc poate fi parametrizată ca
Atunci lungimea arcului de la la este
Aria sectorului
[modificare | modificare sursă]Aria sectorului format dintr-un arc și centrul unui cerc (adică mărginită de arc și de cele două raze trasate din punctele sale finale) este
Aria A are aceeași proporție față de aria cercului ca și unghiul θ față de 2π (respectiv 360°):
Se simplifică π în ambii membri ai relației:
Înmulțind ambii membri cu r2 se obține în final:
Folosind conversia descrisă mai sus, aria sectorului pentru un unghi la centru măsurat în grade este
Aria segmentului
[modificare | modificare sursă]Aria formei delimitate de arc și coardă (linia dreaptă dintre cele două puncte finale ale acestuia) este
Asta se obține scăzând din aria sectorului aria triunghiului format din centrul cercului și cele două puncte de capăt ale arcului de cerc.
Raza
[modificare | modificare sursă]
Folosind puterea punctului față de cerc(d) raza r a cercului se poate calcula din lungimea coardei, W, care subîntinde arcul și înălțimea H. Mediatoarea coardei împarte coarda în două jumătăți egale, fiecare cu lungimea W2. Lungimea diametrului este de 2r și este împărțită în două părți de coardă. Lungimea unei părți este săgeata arcului, H, iar cealaltă parte este restul diametrului, cu lungimea 2r − H. Aplicarea teoremei coardelor care se intersectează la aceste două coarde produce
de unde
prin urmare
Note
[modificare | modificare sursă]- ^ „arc” la DEX online
- ^ a b Tatiana Ceban, Unghi la centru. Arce de cerc. Unghi înscris în cerc. Clasa a VIII–IX-a., livresq.com, 28 iulie 2020, accesat 2021-08-28
- ^ en Larson, R., & Edwards, B. H., Calculus I with Precalculus, Boston: Brooks/Cole, 2002), p. 570
Legături externe
[modificare | modificare sursă] Materiale media legate de arc de cerc la Wikimedia Commons
Materiale media legate de arc de cerc la Wikimedia Commons- en Table of contents for Math Open Reference Circle pages
- en Math Open Reference page on circular arcs With interactive animation
- en Math Open Reference page on Radius of a circular arc or segment With interactive animation
- en Eric W. Weisstein, Arc la MathWorld.





![{\displaystyle {\begin{aligned}{\frac {60}{360}}&={\frac {L}{24}}\\[6pt]360L&=1440\\[6pt]L&=4{\text{ m.}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b0aedcc2b9bacaf77e672abd71296256d8ab42f)



![{\displaystyle L=r{\Big [}\arcsin \left({\frac {x}{r}}\right){\Big ]}_{a}^{b}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9af06c827ad36f4ee0925c92a649cf2280205642)













