Construcția Wythoff

În geometrie o construcție Wythoff, numită astfel după matematicianul Willem Abraham Wythoff, este o metodă de construire a unui poliedru uniform sau a pavărilor plane. Este adesea denumită construcția caleidoscopică a lui Wythoff.

Metoda de construcție[modificare | modificare sursă]

Metoda se bazează pe ideea de pavare a unei sfere, cu triunghiuri sferice — vezi triunghi Schwarz. Această construcție aranjează trei oglinzi pe laturile unui triunghi, ca într-un caleidoscop. Totuși, diferit de un caleidoscop, oglinzile nu sunt paralele, ci se intersectează, într-un punct. Prin urmare, ele definesc un triunghi sferic pe suprafața oricărei sfere cu centrul în acel punct și reflexiile repetate produc o multitudine de copii ale triunghiului. Dacă unghiurile triunghiului sferic sunt alese corespunzător, triunghiurile vor pava sfera, o dată sau de mai multe ori.

Dacă se plasează un vârf într-un punct potrivit în interiorul triunghiului sferic închis de oglinzi, este posibil să se asigure că reflexiile acelui punct produc un poliedru uniform. Pentru un triunghi sferic ABC avem patru posibilități care vor produce un poliedru uniform:

Un vârf este plasat în punctul A. Acest lucru produce un poliedru cu simbolul Wythoff a|b c, unde a este egal cu $π$ împărțit la unghiul A al triunghiului și similar pentru b și c.
Un vârf este plasat într-un punct de pe dreapta AB aflat pe bisectoarea unghiului C. Aceasta produce un poliedru cu simbolul Wythoff a b|c.
Un vârf este plasat astfel încât să fie în centrul cercului înscris în triunghiul ABC. Aceasta produce un poliedru cu simbolul Wythoff a b c|.
Vârful se află într-un punct astfel încât, atunci când este rotit în jurul oricărui colț al triunghiului cu de două ori unghiul în acel punct, este deplasat cu aceeași distanță față de fiecare unghi. Sunt folosite doar reflexiile cu numere pare ale vârfului original. Poliedrul are simbolul Wythoff |a b c.

În general, metoda se aplică și pentru politopurile regulate din dimensiuni mai mari, inclusiv politopurile uniforme^⁠(d) cvadridimensionale.

Exemple
Prismă hexagonală, construită din ambele familii (6 2 2) și (3 2 2).	Pavare pătrată trunchiată, construită prin două poziții de simetrie diferite în familia (4 4 2).	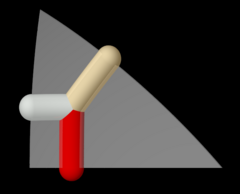Simbol Wythoff pq2\| = 432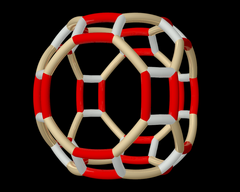\|. Orbita modelului Wythoff de mai sus sub acțiunea simetriei octaedrice.

Construcții newythoffiene[modificare | modificare sursă]

Politopurile uniforme care nu pot fi create prin oglindiri conform construcției Wythoff sunt numite newythoffiene. În general, ele pot fi obținute din formele wythoffiene fie prin alternări (omiterea alternativă a vârfurilor), fie prin inserarea de straturi alternate de figuri parțiale. Ambele tipuri de figuri vor avea simetrie de rotație. Uneori, formele snub sunt considerate wythoffiene, chiar dacă pot fi construite doar prin alternarea formelor omnitrunchiate.

Exemple
Antiprismă hexagonală, construită prin alternarea unei prisme dodecagonale.	Pavare triunghiulară alungită, construită stratificat din rînduri de pavare pătrată și pavare triunghiulară.	Marele dirombicosidodecaedru este singurul poliedru uniform newythoffian.

Bibliografie[modificare | modificare sursă]

en Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN: 0-486-61480-8 (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction)
en Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN: 0-486-40919-8 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
en Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. [1] Arhivat în 2 ianuarie 2004, la Wayback Machine. (Section 4: The Kaleidoscope)
en W.A. Wythoff, A relation between the polytopes of the C600-family, Koninklijke Akademie van Wetenschappen te Amsterdam, Proceedings of the Section of Sciences, 20 (1918) 966–970.