Diagramă Coxeter–Dynkin

Diagramele Coxeter–Dynkin ale grupurilor Coxeter finite fundamentale

Diagramele Coxeter–Dynkin ale grupurilor Coxeter afine fundamentale

În geometrie, o diagramă Coxeter–Dynkin (sau diagramă Coxeter, graf Coxeter) este un graf cu muchii marcate cu numere (numite ramuri) reprezentând relațiile spațiale dintre o colecție de oglinzi (sau hiperplane de reflexie). Descrie o construcție caleidoscopică: fiecare nod al grafului reprezintă o oglindă (fațetă a domeniului) și eticheta atașată unei ramuri codifică ordinul unghiului diedru între două oglinzi (pe o față a domeniului), care este raportul dintre 180° și unghiul dintre planele oglinzilor. O ramură neetichetată reprezintă implicit ordinul 3 (60°).

Fiecare diagramă reprezintă un grup Coxeter, iar grupurile Coxeter sunt clasificate după diagramele lor asociate.

Diagramele Dynkin sunt obiecte strâns legate, care diferă de diagramele Coxeter în două privințe: în primul rând, ramurile etichetate cu "4" sau mai mult sunt orientate, în timp ce diagramele Coxeter sunt neorientate; în al doilea rând, diagramele Dynkin trebuie să satisfacă o restricție suplimentară (cristalografică), și anume că singurele etichete permise ale ramurilor sunt 2, 3, 4 și 6. Diagramele Dynkin corespund și sunt utilizate pentru a clasifica sistemele de rădăcini și, prin urmare, algebra Lie semisimplă.

Descriere

Ramurile unei diagrame Coxeter–Dynkin sunt etichetate cu un număr rațional p, reprezentând un unghi diedru de 180°/p. p = 2 unghiul este de 90° și oglinzile nu au nicio interacțiune, astfel încât ramura poate fi omisă din diagramă. Dacă o ramură este nemarcată, se presupune că are p = 3, reprezentând un unghi de 60°. Două oglinzi paralele au o ramură marcată cu "∞". În principiu, n oglinzi pot fi reprezentate printr-un graf complet în care sunt trasate toate cele n(n − 1) / 2 ramuri. În practică, aproape toate configurațiile interesante ale oglinzilor includ un număr de unghiuri drepte, astfel încât ramurile corespunzătoare sunt omise.

Diagramele pot fi etichetate după structura grafului lor. Primele forme studiate de Ludwig Schläfli sunt ortoscheme care au grafuri liniare care generează politopuri regulate și faguri regulați. Plagioschemele sunt simplexuri reprezentate prin grafuri ramificate, iar cicloschemele sunt simplexuri reprezentate prin grafuri ciclice.

Matricea Schläfli

Orice diagramă Coxeter are o matrice Schläfli corespunzătoare (așa numită după Ludwig Schläfli), cu elementele a_i,j = a_j,i = −2cos (π / p) unde p este ordinul ramurilor dintre perechile de oglinzi. Ca matrice de cosinusuri, este numită și matrice Gramian după Jørgen Pedersen Gram. Toate matricile Schläfli ale grupurilor Coxeter sunt simetrice deoarece vectorii lor rădăcină sunt normalizați. Este legată îndeaproape de matricea Cartan, utilizată în graful similar dar orientat, diagrama Dynkin în cazurile cu p = 2, 3, 4 și 6, care NU sunt simetrice în general.

Determinantul matricei Schläfli, numit Schläflian, și semnul său determină dacă grupul este finit (pozitiv), afin (zero) sau nedefinit (negativ). Această regulă se numește Criteriul lui Schläfli.

Valorile proprii ale matricei Schläfli determină dacă un grup Coxeter este de tip finit (toate pozitive), de tip afin (toate nenegative, cel puțin una fiind zero) sau de tip nedefinit (altfel). Tipul nedefinit este uneori subdivizat, de ex. în grupuri Coxeter hiperbolice și alte grupuri Coxeter. Totuși, există mai multe definiții neechivalente pentru grupurile Coxeter hiperbolice. În articol se folosește următoarea definiție: Un grup Coxeter cu diagramă conectată este hiperbolic dacă nu este nici de tip finit, nici afin, dar fiecare subdiagramă conectată adecvat este de tip finit sau afin. Un grup Coxeter hiperbolic este compact dacă toate subgrupurile sunt finite (adică au determinanți pozitivi) și paracompact dacă toate subgrupurile sale sunt finite sau afine (adică au determinanți negativi).

Grupurile finite și afine sunt numite și eliptice, respectiv parabolice. Grupurile hiperbolice se mai numesc și Lannér, după F. Lannér care a enumerat grupurile hiperbolice compacte în 1950, și Koszul (sau cvasi-Lannér) pentru grupurile paracompacte.

Grupuri Coxeter de ordinul 2

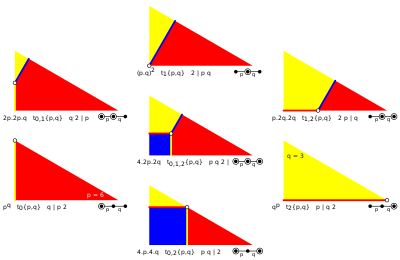
La ordinul 2, tipul unui grup Coxeter este complet determinat de determinantul matricei Schläfli, deoarece este pur și simplu produsul valorilor proprii: tip finit (determinant pozitiv), tip afin (determinant zero) sau hiperbolic (determinant negativ). Coxeter folosește o notație cu paranteze echivalentă care afișează o secvență cu ordinea ramurilor ca înlocuitor pentru diagramele grafice nod-ramură. Există și soluții raționale [p/q], , cu cmmdc(p, q) = 1, care definesc domenii fundamentale suprapuse. De exemplu, 3/2, 4/3, 5/2, 5/3, 5/4. și 6/5.

Tip	Finit					Afin	Hiperbolic
Geometrie					...
Coxeter	[ ]	[2]	[3]	[4]	[p]	[∞]	[∞]	[iπ/λ]
Ordin	2	4	6	8	2p	∞
Liniile de reflexie sunt colorate pentru a corespunde nodurilor diagramei Coxeter. Domeniile fundamentale sunt colorate alternativ.

Grupuri Coxeter de ordinul 2
Ordin p	Grup	diagramă Coxeter		matrice Schläfli
				$\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]$	Determinant (4-a21*a12)
Finite (determinant > 0)
2	I2(2) = A1xA1		[2]	$\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]$	4
3	I2(3) = A2		[3]	$\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]$	3
3/2			[3/2]	$\left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]$
4	I2(4) = B2		[4]	$\left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]$	2
4/3			[4/3]	$\left[{\begin{smallmatrix}2&{\sqrt {2}}\\{\sqrt {2}}&2\end{smallmatrix}}\right]$
5	I2(5) = H2		[5]	$\left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]$	$(5-{\sqrt {5}})/2$ ~1.38196601125
5/4			[5/4]	$\left[{\begin{smallmatrix}2&\phi \\\phi &2\end{smallmatrix}}\right]$
5/2			[5/2]	$\left[{\begin{smallmatrix}2&1-\phi \\1-\phi &2\end{smallmatrix}}\right]$	$(5+{\sqrt {5}})/2$ ~3.61803398875
5/3			[5/3]	$\left[{\begin{smallmatrix}2&\phi -1\\\phi -1&2\end{smallmatrix}}\right]$
6	I2(6) = G2		[6]	$\left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]$	1
6/5			[6/5]	$\left[{\begin{smallmatrix}2&{\sqrt {3}}\\{\sqrt {3}}&2\end{smallmatrix}}\right]$
8	I2(8)		[8]	$\left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {2}}}}\\-{\sqrt {2+{\sqrt {2}}}}&2\end{smallmatrix}}\right]$	$2-{\sqrt {2}}$ ~0.58578643763
10	I2(10)		[10]	$\left[{\begin{smallmatrix}2&-{\sqrt {(5+{\sqrt {5}})/2}}\\-{\sqrt {(5+{\sqrt {5}})/2}}&2\end{smallmatrix}}\right]$	$(3-{\sqrt {5}})/2$ ~0.38196601125
12	I2(12)		[12]	$\left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {3}}}}\\-{\sqrt {2+{\sqrt {3}}}}&2\end{smallmatrix}}\right]$	$2-{\sqrt {3}}$ ~0.26794919243
p	I2(p)		[p]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /p)$
Afin (determinant = 0)
∞	I2(∞) = ${\tilde {I}}_{1}$ = ${\tilde {A}}_{1}$		[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
Hiperbolice (determinant ≤ 0)
∞			[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
∞			[iπ/λ]	$\left[{\begin{smallmatrix}2&-2cosh(2\lambda )\\-2cosh(2\lambda )&2\end{smallmatrix}}\right]$	$-4\sinh ^{2}(2\lambda )\leq 0$

Vizualizări geometrice

Diagrama Coxeter–Dynkin poate fi văzută ca o descriere grafică a domeniului fundamental al oglinzilor. O oglindă reprezintă un hiperplan într-un spațiu dimensional sferic sau euclidian sau hiperbolic dat. (În spațiile 2D, o oglindă este o dreaptă, iar în 3D o oglindă este un plan).

Aceste vizualizări arată domeniile fundamentale pentru grupurile euclidiene 2D și 3D, și grupurile sferice 2D. Pentru fiecare diagrama Coxeter poate fi dedusă prin identificarea hiperplanelor oglindă și etichetarea conectivității acestora, ignorând unghiurile diedrice de 90° (ordinul 2).

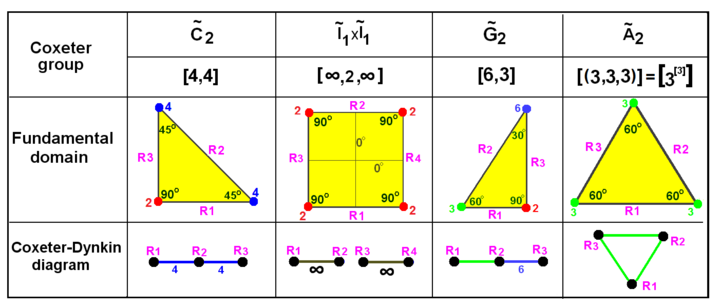Grupuri Coxeter în planul euclidian cu diagrame echivalente. Reflexiile sunt etichetate ca noduri ale grafurilor: R1, R2 etc. și sunt colorate după ordinea lor de reflexie. Reflexiile la 90° sunt inactive, prin urmare sunt eliminate din diagramă. Oglinzile paralele sunt conectate printr-o ramură etichetată ∞. Grupul prismatic ${\tilde {I}}_{1}$x${\tilde {I}}_{1}$ este afișat ca o dublare a ${\tilde {C}}_{2}$, dar pot fi create și ca domenii dreptunghiulare de la dublarea triunghiurilor ${\tilde {G}}_{2}$. ${\tilde {A}}_{2}$ este o dublare a triunghiului ${\tilde {G}}_{2}$.
Multe grupuri Coxeter din planul hiperbolic pot fi obținute din cazurile euclidiene ca o serie de soluții hiperbolice.
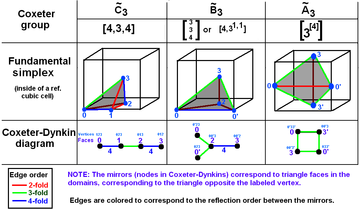Grupuri Coxeter în spațiul tridimensional cu diagrame. Oglinzile (fețele triunghiului) sunt etichetate de vârful opus 0..3. Ramurile sunt colorate după ordinea lor de reflexie. ${\tilde {C}}_{3}$ umple 1/48 din cub. ${\tilde {B}}_{3}$ umple 1/24 din cub. ${\tilde {A}}_{3}$ umple 1/12 din cub.	Grupuri Coxeter în sferă cu diagrame echivalente. Un domeniu fundamental este conturat în galben. Vârfurile domeniului (și ramurile grafurilor) sunt colorate după ordinea lor de reflexie.

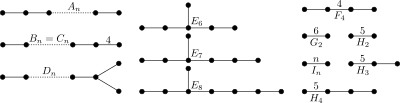
Grupuri Coxeter finite

• Trei simboluri diferite sunt date pentru aceleași grupuri — ca literă/număr, ca set de numere între paranteze și ca diagramă Coxeter.
• Grupurile bifurcate D_n sunt versiunea înjumătățită sau alternată a grupurilor regulate C_n.
• Grupurile bifurcate D_n și E_n sunt, de asemenea, etichetate cu o notație cu exponenți [3^a,b,c] undea,b,csunt numărul de segmente din fiecare din cele trei ramuri.

Diagramele Coxeter–Dynkin finite conectate (de ordinul 1 la 9)

Ordin	Grupuri Lie simple			Grupuri Lie excepționale
	${A}_{1+}$	${B}_{2+}$	${D}_{2+}$	${E}_{3-8}$	${F}_{3-4}$	${G}_{2}$	${H}_{2-4}$	${I}_{2}(p)$
1	A1=[ ]
2	A2=[3]	B2=[4]	D2=A1A1			G2=[6]	H2=[5]	I2[p]
3	A3=[32]	B3=[3,4]	D3=A3	E3=A2A1	F3=B3		H3
4	A4=[33]	B4=[32,4]	D4=[31,1,1]	E4=A4	F4		H4
5	A5=[34]	B5=[33,4]	D5=[32,1,1]	E5=D5
6	A6=[35]	B6=[34,4]	D6=[33,1,1]	E6=[32,2,1]
7	A7=[36]	B7=[35,4]	D7=[34,1,1]	E7=[33,2,1]
8	A8=[37]	B8=[36,4]	D8=[35,1,1]	E8=[34,2,1]
9	A9=[38]	B9=[37,4]	D9=[36,1,1]
10+	...	...	...	...

Aplicarea la politopuri uniforme

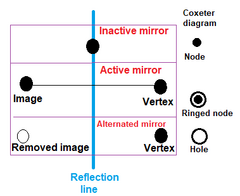La construcția politopurilor uniforme, nodurile sunt marcate ca active de un inel dacă punctul generator se află în afara oglinzii, creând o nouă latură între punctul generator și imaginea sa oglindă. Un nod fără inel reprezintă o oglindă inactivă care nu generează puncte noi. Un inel fără nod se numește gaură.

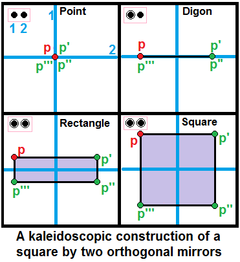Două oglinzi ortogonale pot fi utilizate pentru a genera un pătrat, , marcat aici cu un punct roșu generator și 3 copii virtuale în oglinzi. Generatorul trebuie să fie dezactivat de ambele oglinzi în acest caz ortogonal pentru a genera un interior. Marcarea inelului presupune că inelele active au generatoare la distanță egală de toate oglinzile, în timp ce un dreptunghi poate reprezenta și o soluție neuniformă.

Diagramele Coxeter–Dynkin pot descrie în mod explicit aproape toate clasele de politopuri uniforme și teselări uniforme. Fiecare politop uniform cu simetrie de reflexie pură (toate, cu excepția câtorva cazuri particulare, au simetrie de reflexie pură) poate fi reprezentat printr-o diagramă Coxeter–Dynkin cu permutări ale notațiilor. Fiecare politop uniform poate fi generat folosind astfel de oglinzi și un singur punct generator: imaginile în oglindă creează puncte noi ca reflexii, apoi laturile politopului pot fi definite între puncte și punctele imagini în oglindă. Fețele sunt generate de reflectarea repetată a unei laturi care eventual se înfășoară în jurul punctului generator inițial; forma finală, precum și orice fațete din dimensiunile superioare, sunt create în mod similar prin reflectarea feței pentru a închide o zonă.

Pentru a specifica vârful generator, unul sau mai multe noduri sunt marcate cu inele, ceea ce înseamnă că vârful nu este pe oglinzile reprezentate de nodul/nodurile inelate. (Dacă sunt marcate două sau mai multe oglinzi, vârful este echidistant de ele.) O oglindă este activă (creează reflexii) numai pentru punctele care nu se află pe ea. O diagramă are nevoie de cel puțin un nod activ pentru a reprezenta un politop. O diagramă neconectată (subgrupuri separate prin ramuri de ordinul 2 sau oglinzi ortogonale) necesită cel puțin un nod activ în fiecare subgraf.

Toate politopurile regulate, reprezentate prin simbolul Schläfli $\left\{p,q,r,...\right\}\,$, pot avea domeniile lor fundamentale reprezentate de un set de n oglinzi cu o diagramă Coxeter–Dynkin aferentă a unei linii de noduri și ramuri etichetate cu $p,q,r,...\,$ cu primul nod inelat.

Politopurile uniforme cu un inel corespund punctelor generatoare în colțurile simplexului domeniului fundamental. Două inele corespund laturilor simplexului și au un grad de libertate, cu doar punctul de mijloc ca soluție uniformă pentru lungimi ale laturilor egale. În general k-punctele generatoare inelate sunt pe (k–1)-fețele simplexului, iar dacă toate nodurile sunt inelate, punctul generator se află în interiorul simplexului.

Cazul particular al politopurilor uniforme cu simetrie nereflexivă este reprezentat de un marcaj secundar în care punctul central al unui nod inelat este eliminat (numit gaură). Aceste forme sunt alternări ale politopurilor cu simetrie de reflexie, ceea ce înseamnă că nodurile alternate sunt șterse. Politopul rezultat va avea o subsimetrie a grupului Coxeter inițial. O alternare trunchiată se numește snub.

Există 7 construcții uniforme reflexive pe baza unui triunghi general, bazate pe 7 poziții generatoare topologice în domeniul fundamental. Fiecare oglindă activă generează o latură, cu două oglinzi active există generatoare pe laturile domeniului și cu trei oglinzi active generatorul este în interior. Unul sau două grade de libertate pot fi tratate astfel încât poziția rezultată să genereze laturi egale ale poliedrului sau ale plăcilor rezultate.

Exemple: 7 generatoare pe simetrie octaedrică, cu domeniul fundamental triunghiul (4 3 2), cu a 8-a generare snub ca alternare.

• Un singur nod reprezintă o singură oglindă. Aceasta se numește grupul A₁. Dacă este inelat, el creează un segment de dreaptă perpendicular pe oglindă, reprezentat ca {}.
• Două noduri neconectate reprezintă două oglinzi perpendiculare. Dacă ambele noduri sunt inelate, se poate crea un dreptunghi sau, dacă punctul este la distanță egală de ambele oglinzi, un pătrat.
• Două noduri conectate printr-o ramură de ordinul n poate crea un n-gon dacă punctul este pe o singură oglindă și un 2n-gon dacă punctul este în afara ambelor oglinzi. Aceasta formează grupul I₁(n).
• Două oglinzi paralele pot reprezenta un grup poligonal infinit I₁(∞), numit și Ĩ₁.
• Trei oglinzi dispuse într-un triunghi formează imagini ca acelea văzute într-un caleidoscop tradițional și pot fi reprezentate prin trei noduri conectate într-un triunghi. Exemplele repetate vor avea ramuri etichetate ca (3 3 3), (2 4 4), (2 3 6), deși ultimele două pot fi trasate ca o linie (cu ramurile 2 ignorate). Acestea vor genera pavări uniforme.
• Trei oglinzi pot genera poliedre uniforme (cu simetrie octaedrică Oh); numerele raționale oferă mulțimea triunghiurilor Schwarz.
• Trei oglinzi cu una perpendiculară pe celelalte două pot forma prisme uniforme.

Dualele politopurilor uniforme sunt uneori marcate cu o bară perpendiculară care înlocuiește nodurile inelate și o gaură barată pentru găurile nodurilor snub. De exemplu, reprezintă un dreptunghi (prin două oglinzi ortogonale active), iar reprezintă poligonul său dual, rombul.

Exemple de poliedre și pavări

De exemplu, grupul Coxeter B₃ are diagrama: . Aceasta este numită și simetrie octaedrică.

Există 7 poliedre uniforme convexe care pot fi construite din acest grup de simetrie și 3 din subsimetriile sale alternate, fiecare cu o diagramă Coxeter–Dynkin marcată în mod unic. Simbolul Wythoff reprezintă un caz special al diagramei Coxeter pentru grafurile de ordinul 3, cu toate cele 3 ordine ale ramurilor denumite, în loc de suprimarea ramurilor de ordinul 2. Simbolul Wythoff este capabil să gestioneze forma snub, dar nu alternări generale fără toate nodurile inelate.

Poliedre octaedrice uniforme
Simetrie: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= sau	= sau	=
Dualele celor de mai sus
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Aceleași construcții pot fi făcute pe grupuri Coxeter disjuncte (ortogonale), cum ar fi prismele uniforme, și pot fi văzute mai clar ca pavări sferice ale diedrelor și hosoedrelor, ca familia [6]×[] sau [6.2]:

Poliedre sferice diedrice hexagonale uniforme
Simetrie: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Dualele celor de mai sus
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Prin comparație, familia [6,3], produce un set paralel de 7 pavări uniforme ale planului euclidian și pavările lor duale. Există din nou 3 alternări și unele versiuni cu simetria la jumătate.

Pavări hexagonale/triunghiulare uniforme
Simetrie: [6,3], (*632)							[6,3]+ (632)	[6,3+] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}
63	3.122	(3.6)2	6.6.6	36	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Dualele celor de mai sus
V63	V3.122	V(3.6)2	V63	V36	V3.4.6.4	V.4.6.12	V34.6	V36

În planul hiperbolic [7,3], familia produce un set paralel de pavări uniforme și pavările lor duale. Există doar o singură alternare snub deoarece toate ordinele ramurilor sunt impare. Există multe alte familii de pavări uniforme în planul hiperbolic.

Pavări heptagonale/triunghiulare uniforme
Simetrie: [7,3], (*732)							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	t{3,7}	{3,7}	rr{7,3}	tr{7,3}	sr{7,3}
Dualele celor de mai sus
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

Grupuri Coxeter afine

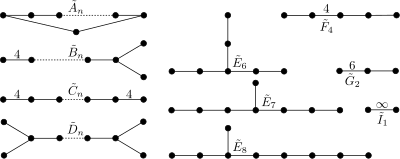
Familii de teselări euclidiene uniforme convexe sunt definite de grupurile Coxeter afine. Aceste grupuri sunt identice cu grupurile finite, cu adăugarea unui nod. În notațiile literale li se dă aceeași literă cu o „~” deasupra literei. Indicele se referă la grupul finit, deci ordinul este indicele plus 1. (Simbolurile Ernst Witt pentru grupurile afine sunt menționate în lista următoare în paranteze.)

1. ${\tilde {A}}_{n-1}$: diagramele de acest tip sunt cicluri. (P_n)
2. ${\tilde {C}}_{n-1}$ este asociat cu familia teselărilor regulate hipercubice $\left\{p,q,r,...\right\}\,$. (R_n)
3. ${\tilde {B}}_{n-1}$ este legat de C, fără una dintre oglinzi. (S_n)
4. ${\tilde {D}}_{n-1}$ este legat de C, fără două dintre oglinzi. (Q_n)
5. ${\tilde {E}}_{6}$, ${\tilde {E}}_{7}$, ${\tilde {E}}_{8}$. (T₇, T₈, T₉)
6. ${\tilde {F}}_{4}$ formează teselarea regulată {3,4,3,3}. (U₅)
7. ${\tilde {G}}_{2}$ formează domeniile fundamentale triunghiulare 30-60-90. (V₃)
8. ${\tilde {I}}_{1}$ = ${\tilde {A}}_{1}$ = ${\tilde {C}}_{1}$ sunt două oglinzi paralele. (W₂)

De asemenea, grupurile compuse pot fi definite ca proiecții ortogonale. Cea mai obișnuită utilizare ${\tilde {A}}_{1}$, ca și ${\tilde {A}}_{1}^{2}$, reprezintă domenii pătrate sau dreptunghiulare în formă de tablă de șah în planul euclidian. Iar ${\tilde {A}}_{1}{\tilde {G}}_{2}$ reprezintă domeniile fundamentale al prismei triunghiulare în spațiul euclidian tridimensional.

Grafuri Coxeter afine pentru 2–10 noduri

Ordin	${\tilde {A}}_{1+}$ (P2+)	${\tilde {B}}_{3+}$ (S4+)	${\tilde {C}}_{1+}$ (R2+)	${\tilde {D}}_{4+}$ (Q5+)	${\tilde {E}}_{n}$ (Tn+1) / ${\tilde {F}}_{4}$ (U5) / ${\tilde {G}}_{2}$ (V3)
2	${\tilde {A}}_{1}$=[∞]		${\tilde {C}}_{1}$=[∞]
3	${\tilde {A}}_{2}$=[3[3]] *		${\tilde {C}}_{2}$=[4,4] *		${\tilde {G}}_{2}$=[6,3] *
4	${\tilde {A}}_{3}$=[3[4]] *	${\tilde {B}}_{3}$=[4,31,1] *	${\tilde {C}}_{3}$=[4,3,4] *	${\tilde {D}}_{3}$=[31,1,3−1,31,1] = ${\tilde {A}}_{3}$
5	${\tilde {A}}_{4}$=[3[5]] *	${\tilde {B}}_{4}$=[4,3,31,1] *	${\tilde {C}}_{4}$=[4,32,4] *	${\tilde {D}}_{4}$=[31,1,1,1] *	${\tilde {F}}_{4}$=[3,4,3,3] *
6	${\tilde {A}}_{5}$=[3[6]] *	${\tilde {B}}_{5}$=[4,32,31,1] *	${\tilde {C}}_{5}$=[4,33,4] *	${\tilde {D}}_{5}$=[31,1,3,31,1] *
7	${\tilde {A}}_{6}$=[3[7]] *	${\tilde {B}}_{6}$=[4,33,31,1]	${\tilde {C}}_{6}$=[4,34,4]	${\tilde {D}}_{6}$=[31,1,32,31,1]	${\tilde {E}}_{6}$=[32,2,2]
8	${\tilde {A}}_{7}$=[3[8]] *	${\tilde {B}}_{7}$=[4,34,31,1] *	${\tilde {C}}_{7}$=[4,35,4]	${\tilde {D}}_{7}$=[31,1,33,31,1] *	${\tilde {E}}_{7}$=[33,3,1] *
9	${\tilde {A}}_{8}$=[3[9]] *	${\tilde {B}}_{8}$=[4,35,31,1]	${\tilde {C}}_{8}$=[4,36,4]	${\tilde {D}}_{8}$=[31,1,34,31,1]	${\tilde {E}}_{8}$=[35,2,1] *
10	${\tilde {A}}_{9}$=[3[10]] *	${\tilde {B}}_{9}$=[4,36,31,1]	${\tilde {C}}_{9}$=[4,37,4]	${\tilde {D}}_{9}$=[31,1,35,31,1]
11	...	...	...	...

Grupuri Coxeter hiperbolice

Există multe grupuri Coxeter hiperbolice infinite. Grupurile hiperbolice sunt clasificate ca fiind compacte sau nu, grupurile compacte având domenii fundamentale delimitate. Grupurile hiperbolice compacte de simplexuri (simplexuri Lannér) există de ordinele 3 – 5. Grupurile paracompacte de simplexuri (simplexuri Koszul) există până la ordinul 10. Grupurile hipercompacte (politopurile Vinberg) au fost explorate, dar nu sunt explorate complet. În 2006, Allcock a demonstrat că există infinit de multe politopuri Vinberg compacte pentru dimensiuni până la 6 și infinit de multe politopuri Vinberg cu volum finit pentru dimensiuni până la 19, astfel că o enumerare completă nu este posibilă. Toate aceste domenii reflexive fundamentale, atât simpliciale cât și nesimpliciale, sunt adesea numite politopuri Coxeter sau uneori mai puțin precis poliedre Coxeter.

Grupuri hiperbolice în H²

Modelul discului Poincaré, domeniul fundamental triunghiuri

Exemple cu triunghiuri dreptunghice [p,q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
Exemple cu triunghiuri oarecare [(p,q,r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

Grupul triunghiular hiperbolic bidimensional există ca diagrame Coxeter de ordinul 3, definite prin triunghiul (p q r) pentru:

${\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1$.

Există infinit de multe grupuri Coxeter hiperbolice compacte triunghiulare, care conțin grafuri liniare și triunghiulare. Grafurile liniare există pentru triunghiurile dreptunghice (cu r=2).

Grupuri Coxeter hiperbolice compacte

Liniar	Ciclic
∞ [p,q], : 2(p+q)<pq ... ... ...	∞ [(p,q,r)], : p+q+r>9 ...

Grupurile Coxeter paracompacte de ordinul 3
există ca limită a celor compacte.

Grafuri liniare	Grafuri ciclice
[p,∞] [∞,∞]	[(p,q,∞)] [(p,∞,∞)] [(∞,∞,∞)]

Grupul triunghiular aritmetic

Grupurile triunghiulare hiperbolice care sunt și grupuri aritmetice formează o submulțime finit. Lista completă a fost făcută cu ajutorul calculatorului de Kisao Takeuchi în lucrarea sa din 1977 Arithmetic triangle groups (română Grupuri triunghiulare aritmetice). Există 85 în total, 76 compacte și 9 paracompacte.

Triunghiuri dreptunghice (p q 2)	Triunghiuri oarecare (p q r)
Grupuri compacte: (76) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Triunghiuri dreptunghice paracompacte: (4) , , ,	Triunghiuri oarecare: (39) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Triunghiuri oarecare paracompacte: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30) (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30) (2 6 6), (2 6 8), (2 6 12) (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18) (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18) (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15) (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12) (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16) (5 5 5), (5 5 10), (5 5 15), (5 10 10) (6 6 6), (6 12 12), (6 24 24) (7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15) (3,3 ∞) (3 ∞ ∞) (4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

Grupuri ale poligoanelor hiperbolice altele decât triunghiurile

Domenii fundamentale ale grupurilor patrulatere

or [∞,3,∞] [iπ/λ1,3,iπ/λ2] (*3222)	or [((3,∞,3)),∞] [((3,iπ/λ1,3)),iπ/λ2] (*3322)	or [(3,∞)[2]] [(3,iπ/λ1,3,iπ/λ2)] (*3232)	or [(4,∞)[2]] [(4,iπ/λ1,4,iπ/λ2)] (*4242)	(*3333)
Domenii cu vârfuri ideale
[iπ/λ1,∞,iπ/λ2] (*∞222)	(*∞∞22)	[(iπ/λ1,∞,iπ/λ2,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

Alte caleidoscoape hiperbolice H² pot fi construite din poligoane de ordin superior. La fel ca grupul triunghiular aceste caleidoscoape pot fi identificate printr-o secvență ciclică a ordinii de intersecție a oglinzilor în jurul domeniului fundamental, ca (a b c d ...), sau echivalent în notația orbifold ca *abcd.... Diagramele Coxeter–Dynkin pentru aceste caleidoscoape poligonale pot fi văzute ca domenii fundamentale degenerate de (n−1)-simplexuri, cu o ordine a ramurilor ciclică de ordinul a,b,c... și restul de n*(n–3) / 2 ramuri sunt etichetate ca infinite (∞) reprezentând oglinzile care nu se intersectează. Singurul exemplu nehiperbolic este simetria euclidiană cu patru oglinzi într-un pătrat sau dreptunghi ca , [∞,2,∞] (orbifold *2222). O altă reprezentare a ramurilor pentru oglinzile care nu se intersectează este folosită de Vinberg care notează ramurile infinite cu linii punctate sau întrerupte, astfel încât această diagramă poate fi afișată ca , cu patru ramuri de ordinul 2 suprimate în jurul perimetrului.

De exemplu, un domeniu patrulater (a b c d) va avea două ramuri de ordin infinit care conectează oglinzile ultratraparalele. Cel mai mic exemplu hiperbolic este , [∞,3,∞] saur [iπ/λ₁,3,iπ/λ₂] (orbifold *3222), unde (λ₁, λ₂) sunt distanța dintre oglinzile ultraparalele. Expresia alternativă este , cu trei ramuri de ordinul 2 suprimate în jurul perimetrului. Similar (2 3 2 3) (orbifold *3232) poate fi reprezentat ca , iar (3 3 3 3), (orbifold *3333) poate fi reprezentat ca un graf complet .

Cel mai înalt domeniu patrulater (∞ ∞ ∞ ∞) este un pătrat infinit, reprezentat printr-un graf tetraedric complet 4 ramuri pe perimetru ca vârfuri ideale și două ramuri diagonale infinite (prezentate ca linii punctate) pentru oglinzi ultraparalele: .

Compacte (grupuri simpliciale Lannér)

Grupurile hiperbolice compacte se numesc grupuri Lannér după Folke Lannér care le-a studiat prima dată în 1950. Ele există doar sub forma grafurilor de ordinul 4 și 5. Coxeter a studiat grupurile Coxeter hiperbolice liniare în lucrarea sa din 1954 Regular Honeycombs in hyperbolic space (română Faguri regulați în spațiul hiperbolic), care conțin două soluții raționale în 4-spațiul hiperbolic: [5/2,5,3,3] = și [5,5/2,5,3] = .

Ordinele 4–5

Domeniul fundamental al oricăruia dintre cele două grupuri bifurcante, [5,3^1,1] și [5,3,3^1,1], este dublu față de cel al unui grup liniar corespunzător, [5,3,4] și respectiv [5,3,3,4]. Notațiile literale au fost date de Norman Johnson ca extensii ale simbolurilor Witt.

Grupuri Coxeter hiperbolice compacte

Dimensiune Hd	Ordin	Nr. total	Liniar	Bifurcat	Ciclic
H3	4	9	3: ${\overline {BH}}_{3}$ = [4,3,5]: ${\overline {K}}_{3}$ = [5,3,5]: ${\overline {J}}_{3}$ = [3,5,3]:	${\overline {DH}}_{3}$ = [5,31,1]:	${\widehat {AB}}_{3}$ = [(33,4)]:   ${\widehat {AH}}_{3}$ = [(33,5)]:   ${\widehat {BB}}_{3}$ = [(3,4)[2]]: ${\widehat {BH}}_{3}$ = [(3,4,3,5)]: ${\widehat {HH}}_{3}$ = [(3,5)[2]]:
H4	5	5	3: ${\overline {H}}_{4}$ = [33,5]: ${\overline {BH}}_{4}$ = [4,3,3,5]: ${\overline {K}}_{4}$ = [5,3,3,5]:	${\overline {DH}}_{4}$ = [5,3,31,1]:	${\widehat {AF}}_{4}$ = [(34,4)]:

Paracompacte (grupuri simpliciale Koszul)

Un exemplu de pavare apeirogonală de ordinul 3, {∞,3} cu un apeirogon verde și oriciclul său circumscris

Grupurile Coxeter hiperbolice paracompacte (numite și necompacte) conțin subgrupuri afine și au domenii fundamentale simpliciale asimptotice. Cel mai înalt grup Coxeter hiperbolic paracompact este de ordinul 10. Aceste grupuri poartă numele matematicianului francez Jean-Louis Koszul. Sunt numite și grupuri cvasi-Lannér care extind grupurile Lannér compacte. S-a stabilit că lista este completă prin căutare computerizată de către M. Chein și publicată în 1969.

După Vinberg, toate cu excepția a opt dintre aceste 72 de simplexuri compacte paracompacte sunt aritmetice. Două dintre grupurile nearitmetice sunt compacte: și . Celelalte șase grupuri nearitmetice sunt toate paracompacte, cu cinci grupuri tridimensionale , , , , și , și unul 5-dimensional .

Simplexuri ideale

Domeniile fundamentale ideale a , [(∞,∞,∞)] prezentate în modelul discului Poincaré

Există 5 grupuri Coxeter hiperbolice care reprezintă simplexuri ideale, grafuri în care îndepărtarea unui nod oarecare le transformă într-un grup Coxeter afin. Astfel, toate vârfurile acestui simplex ideal sunt la infinit.

Ordin	Grup ideal		Subgrup afin
3	[(∞,∞,∞)]		[∞]
4	[4[4]]		[4,4]
4	[3[3,3]]		[3[3]]
4	[(3,6)[2]]		[3,6]
6	[(3,3,4)[2]]		[4,3,3,4], [3,4,3,3]	,

Ordinele 4–10

Celulele euclidiene infinite, cum ar fi o pavare hexagonală, scalate corespunzător converg într-un singur punct ideal la infinit, ca fagurele pavare hexagonală, {6,3,3}, așa cum se arată cu această singură celulă într-o proiecție a modelului discului Poincaré

Există un total de 58 de grupuri Coxeter hiperbolice paracompacte de la ordinul 4 până la 10. Toate cele 58 sunt grupate mai jos în cinci categorii. Simbolurile literale sunt date de Johnson ca simboluri Witt extinse, folosind PQRSTWUV din simbolurile Witt afine și adăugând LMNOXYZ. Pentru scheme ciclice aceste grupuri hiperbolice primesc o suprabarare sau o acoladă unghiulară. Notația Coxeter cu paranteze este o reprezentare liniarizată a grupului Coxeter.

Grupuri hiperbolice paracompacte

Ordin	Nr. total	Grupuri
4	23	${\widehat {BR}}_{3}$ = [(3,3,4,4)]: ${\widehat {CR}}_{3}$ = [(3,43)]: ${\widehat {RR}}_{3}$ = [4[4]]: ${\widehat {AV}}_{3}$ = [(33,6)]: ${\widehat {BV}}_{3}$ = [(3,4,3,6)]: ${\widehat {HV}}_{3}$ = [(3,5,3,6)]: ${\widehat {VV}}_{3}$ = [(3,6)[2]]:	${\overline {P}}_{3}$ = [3,3[3]]: ${\overline {BP}}_{3}$ = [4,3[3]]: ${\overline {HP}}_{3}$ = [5,3[3]]: ${\overline {VP}}_{3}$ = [6,3[3]]: ${\overline {DV}}_{3}$ = [6,31,1]: ${\overline {O}}_{3}$ = [3,41,1]: ${\overline {M}}_{3}$ = [41,1,1]:	${\overline {R}}_{3}$ = [3,4,4]: ${\overline {N}}_{3}$ = [43]: ${\overline {V}}_{3}$ = [3,3,6]: ${\overline {BV}}_{3}$ = [4,3,6]: ${\overline {HV}}_{3}$ = [5,3,6]: ${\overline {Y}}_{3}$ = [3,6,3]: ${\overline {Z}}_{3}$ = [6,3,6]:	${\overline {DP}}_{3}$ = [3[]x[]]: ${\overline {PP}}_{3}$ = [3[3,3]]:
5	9	${\overline {P}}_{4}$ = [3,3[4]]: ${\overline {BP}}_{4}$ = [4,3[4]]: ${\widehat {FR}}_{4}$ = [(32,4,3,4)]: ${\overline {DP}}_{4}$ = [3[3]x[]]:	${\overline {N}}_{4}$ = [4,3,((4,2,3))]: ${\overline {O}}_{4}$ = [3,4,31,1]: ${\overline {S}}_{4}$ = [4,32,1]:	${\overline {R}}_{4}$ = [(3,4)2]:	${\overline {M}}_{4}$ = [4,31,1,1]:
6	12	${\overline {P}}_{5}$ = [3,3[5]]: ${\widehat {AU}}_{5}$ = [(35,4)]: ${\widehat {AR}}_{5}$ = [(3,3,4)[2]]:	${\overline {S}}_{5}$ = [4,3,32,1]: ${\overline {O}}_{5}$ = [3,4,31,1]: ${\overline {N}}_{5}$ = [3,(3,4)1,1]:	${\overline {U}}_{5}$ = [33,4,3]: ${\overline {X}}_{5}$ = [3,3,4,3,3]: ${\overline {R}}_{5}$ = [3,4,3,3,4]:	${\overline {Q}}_{5}$ = [32,1,1,1]: ${\overline {M}}_{5}$ = [4,3,31,1,1]: ${\overline {L}}_{5}$ = [31,1,1,1,1]:
7	3	${\overline {P}}_{6}$ = [3,3[6]]:	${\overline {Q}}_{6}$ = [31,1,3,32,1]:	${\overline {S}}_{6}$ = [4,32,32,1]:
8	4	${\overline {P}}_{7}$ = [3,3[7]]:	${\overline {Q}}_{7}$ = [31,1,32,32,1]:	${\overline {S}}_{7}$ = [4,33,32,1]:	${\overline {T}}_{7}$ = [33,2,2]:
9	4	${\overline {P}}_{8}$ = [3,3[8]]:	${\overline {Q}}_{8}$ = [31,1,33,32,1]:	${\overline {S}}_{8}$ = [4,34,32,1]:	${\overline {T}}_{8}$ = [34,3,1]:
10	4	${\overline {P}}_{9}$ = [3,3[9]]:	${\overline {Q}}_{9}$ = [31,1,34,32,1]:	${\overline {S}}_{9}$ = [4,35,32,1]:	${\overline {T}}_{9}$ = [36,2,1]:

Relațiile subgrupurilor grupurilor hiperbolice paracompacte

Acești arbori reprezintă relațiile subgrupurilor grupurilor hiperbolice paracompacte. Indicii de subgrup pe fiecare conexiune sunt colorați în roșu. Subgrupurile cu indicele 2 reprezintă o eliminare a oglinzii și dublarea fundamentală a domeniului. Altele pot fi deduse inferând comensurabilitatea (raportul întreg al volumelor) pentru domeniile tetraedrice.

Arborii subgrupului
H3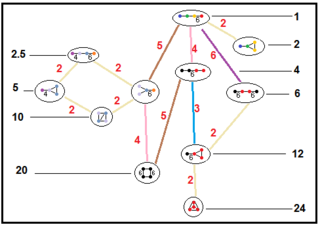
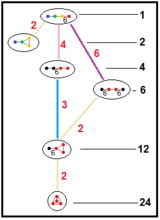
H4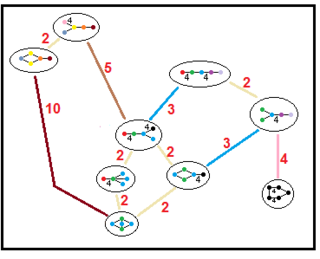
H5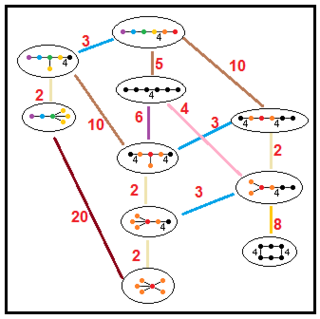

Grupuri Coxeter hipercompacte (politopuri Vinberg)

La fel cum planul hiperbolic H² are domenii poligonale netriunghiulare, există și domenii hiperbolice reflexive cu dimensiuni superioare. Aceste domenii nesimpliciale pot fi considerate simplexuri degenerate cu oglinzi de ordin infinit care nu se intersectează, sau, într-o diagramă Coxeter, astfel de ramuri sunt trasate cu linii punctate sau întrerupte. Aceste domenii nesimpliciale sunt numite politopuri Vinberg, după algoritmul Vinberg pentru găsirea domeniului fundamental nesimplicial al unui grup de reflexie hiperbolică. Geometric, aceste domenii fundamentale pot fi clasificate drept piramide patrulatere, sau prisme sau alte politopuri cu muchii generate de intersecție a două oglinzi având unghiurile diedre de π/n pentru n = 2, 3, 4... .

Într-un domeniu bazat pe un simplex există n+1 oglinzi pentru spațiul n-dimensional. În domeniile nesimpliciale, există mai mult de n+1 oglinzi. Lista este finită, dar nu este complet cunoscută. În schimb, au fost stabilite listele parțiale cu n+k oglinzi pentru k = 2, 3 și 4.

Grupurile Coxeter hipercompacte în spațiile tridimensionale sau mai mult diferă de grupurile bidimensionale într-un aspect esențial. Două n-goane hiperbolice având aceleași unghiuri în aceeași ordine ciclică pot avea laturi de lungimi diferite și nu sunt în general congruente. În schimb, politopurile Vinberg tridimensionale sau mai mult sunt complet determinate de unghiurile diedre. Acest fapt se bazează pe Teorema rigidității Mostow, că două grupuri izomorfe generate de reflexii în Hⁿ pentru n ≥ 3, definesc domenii fundamentale congruente (politopurile Vinberg).

Politopuri Vinberg de ordinul n+2 din spațiul n-dimensional

Lista completă a politopurilor Vinberg hiperbolice compacte cu oglinzi de ordinul "n+2 din spațiul n-dimensional a fost stabilită de F. Esselmann în 1996. O listă parțială a fost publicată în 1974 de I. M. Kaplinskaya. Lista completă a soluțiilor paracompacte a fost publicată de P. Tumarkin în 2003, pentru dimensiuni de la 3 la 17.

Cea mai mică formă paracompactă din H³ poate fi reprezentată de , sau [∞,3,3,∞] care poate fi construită printr-o îndepărtare în oglindă a grupului hiperbolic paracompact [3,4,4] ca [3,4,1⁺,4]. Domeniul fundamental dublat se schimbă de la un tetraedru la o piramidă patrulateră. Alte piramide includ [4,4,1⁺,4] = [∞,4,4,∞], = . Îndepărtarea unei oglinzi din unele dintre graficele Coxeter hiperbolice ciclice devin grafuri papion: [(3,3,4,1⁺,4)] = [((3,∞,3)),((3,∞,3))] sau , [(3,4,4,1⁺,4)] = [((4,∞,3)),((3,∞,4))] or , [(4,4,4,1⁺,4)] = [((4,∞,4)),((4,∞,4))] or .

Alte grafuri paracompacte valide cu domenii fundamentale piramide patrulatere includ:

Dimensiune	Ordin	Grafuri
H3	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

Alt subgrup [1⁺,4^1,1,1] = [∞,4,1⁺,4,∞] = [∞^[6]]. = = .

Politopuri Vinberg de ordinul n+3 din spațiul n-dimensional

Există un număr finit de simplexuri fundamentale degenerate care există până în 8 dimensiuni. Lista completă a politopurilor Vinberg compacte cu oglinzi de ordinul "n+3 pentru spații n-dimensionale a fost stabilită de P. Tumarkin în 2004. Aceste grupuri sunt etichetate prin linii punctate/întrerupte pentru ramurile ultraparalele. Lista completă a politopurilor Vinberg necompacte cu oglinzi de ordinul n+3 și cu un vârf nesimplu din n-dimensiuni a fost stabilită de Mike Roberts.

De la dimensiunile 4 până la 8, grupurile Coxeter de ordinele 7 până 11 sunt enumerate ca 44, 16, 3, 1 și respectiv 1. Cel mai mare a fost descoperit de Bugaenko în 1984 în dimensiunea 8, ordinul 11:

Dimensiuni	Ordin	Cazuri	Grafuri
H4	7	44	...
H5	8	16	..
H6	9	3
H7	10	1
H8	11	1

Politopuri Vinberg de ordinul n+4 din spațiul n-dimensional

Există un număr finit de simplexuri fundamentale degenerate până îa 8 dimensiuni. Politopurile compacte Vinberg cu oglinzi de ordinul "n+4 din spațiul n-dimensional au fost explorate de A. Felikson și P. Tumarkin în 2005.

Grupuri lorentziene

Faguri regulați cu grupuri lorentziene

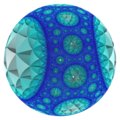{3,3,7} văzut din afara modelului bilei Poincaré

{7,3,3} văzut din afara modelului bilei Poincaré

Grupuri lorentziene de ordinul 5 aranjate ca subgrupuri ale [6,3,3,3] și [6,3,6,3]. Grupul foarte simetric , [3^[3,3,3]] este un subgrup indice 120 al [6,3,3,3]

Grupurile lorentziene pentru domeniile simpliciale pot fi definite ca grafuri dincolo de formele hiperbolice paracompacte. Acestea sunt uneori numite simplexuri superideale și sunt legate de o geometrie lorentziană, numită astfel după Hendrik Lorentz, în domeniul relativității restrânse și generale a spațiu–timpului, conținând una (sau mai multe) componente dimensionale „asemănătoare timpului” ale căror produse scalare proprii sunt negative. Danny Calegari numește acestea grupuri Coxeter cocompacte convexe în spațiul hiperbolic n-dimensional.

O lucrare din 1982 a lui George Maxwell, Sphere Packings and Hyperbolic Reflection Groups (română Împachetarea sferelor și grupuri de reflexie hiperbolice), publică lista completă a lorentzienelor de la ordinul 5 la 11. El le numește de nivel 2, adică eliminarea oricărei permutări a 2 noduri duce la un graf finit sau euclidian. Enumerarea sa este completă, dar nu a enumerat grafurile care sunt un subgrup al altuia. Toate grupurile Coxeter cu ramuri de ordin superior lui 4 sunt lorentziene, terminându-se la limită ca un graf complet 3-simplex diagramă Coxeter–Dynkin cu 6 ramuri de ordin infinit, care poate fi exprimat ca [∞^[3,3]]. Ordinele 5–11 au un număr finit de grupuri 186, 66, 36, 13, 10, 8 și respectiv 4 grupuri lorentziene. Un articol din 2013, H. Chen și J.-P. Labbé, Lorentzian Coxeter groups and Boyd–Maxwell ball packings (română Grupuri Coxeter lorentziene și impachetări ale sferelor Boyd–Maxwell), au recalculat și publicat lista completă.

Pentru ordinele superioare 8–11, listele complete sunt:

Grupuri Coxeter lorentziene

Ordin	Nr. total	Grupuri
4	∞	[3,3,7] ... [∞,∞,∞]: ... [4,3[3]] ... [∞,∞[3]]: ... [5,41,1] ... [∞1,1,1]: ... ... [(5,4,3,3)] ... [∞[4]]: ... ... ... [4[]×[]] ... [∞[]×[]]: ... ... [4[3,3]] ... [∞[3,3]]
5	186	...[3[3,3,3]]:...
6	66
7	36	[31,1,1,1,1,1]: ...
8	13	[3,3,3[6]]: [3,3[6],3]: [3,3[2+4],3]: [3,3[1+5],3]: [3[ ]e×[3]]:	[4,3,3,33,1]: [31,1,3,33,1]: [3,(3,3,4)1,1]: [32,1,3,32,1]:		[4,3,3,32,2]: [31,1,3,32,2]:
9	10	[3,3[3+4],3]: [3,3[9]]: [3,3[2+5],3]:	[32,1,32,32,1]:	[33,1,33,4]: [33,1,3,3,31,1]:	[33,3,2]: [32,2,4]: [32,2,33,4]: [32,2,3,3,31,1]:
10	8	[3,3[8],3]: [3,3[3+5],3]: [3,3[9]]:	[32,1,33,32,1]:	[35,3,1]: [33,1,34,4]: [33,1,33,31,1]:	[34,4,1]:
11	4		[32,1,34,32,1]:	[32,1,36,4]: [32,1,35,31,1]:	[37,2,1]:

Diagrame Coxeter foarte extinse

Uneori se folosesc expresii care particularizează utilizarea directă a diagramei Dynkin. Folosirea diagramelor la grupuri afine este considerată „extinsă” (engleză extended), la grupuri hiperbolice „supraextinsă” (engleză over-extended), iar la grupuri simpliciale „foarte extinsă” (engleză very-extended). Aceste extensii sunt de obicei marcate cu un exponent de 1, 2 sau 3 simboluri „+” pentru numărul de noduri extinse. Această serie extinsă poate fi extinsă înapoi prin eliminarea secvențială a nodurile din aceeași poziție în graf, deși procesul se oprește după îndepărtarea nodului de ramificare. Familia extinsă E₈ este cel mai frecvent exemplu de extindere înapoi la E₃ și înainte spre E₁₁.

Procesul de extindere poate defini o serie limitată de grafuri Coxeter care progresează de la finit la afin, la hiperbolic, la lorentzian. Determinantul matricelor Cartan determină unde seria se schimbă de la finit (pozitiv) la afin (zero) la hiperbolic (negativ) și se termină ca un grup lorentzian, conținând cel puțin un subgrup hiperbolic. Grupurile necristalografice H_n formează o serie extinsă unde H₄ este extensia ca grup hiperbolic compact și supraextensia ca grup lorentzian.

Determinanții matricilor Schläfli sunt:

• det(A₁ⁿ=[2^n-1]) = 2ⁿ (Finit pentru orice n)
• det(A_n=[3^n-1]) = n+1 (Finit pentru orice n)
• det(B_n=[4,3^n-2]) = 2 (Finit pentru orice n)
• det(D_n=[3^n-3,1,1]) = 4 (Finit pentru orice n)

Determinanții matricilor Schläfli din seriile excepționale sunt:

• det(E_n=[3^n-3,2,1]) = 9-n (Finit pentru E₃(=A₂A₁), E₄(=A₄), E₅(=D₅), E₆, E₇ și E₈, afin pentru E₉ (${\tilde {E}}_{8}$), hiperbolic pentru E₁₀)
• det([3^n-4,3,1]) = 2(8-n) (Finit pentru n=4 – 7, afin pentru (${\tilde {E}}_{7}$) și hiperbolic pentru n=8)
• det([3^n-4,2,2]) = 3(7-n) (Finit pentru n=4 – 6, afin pentru (${\tilde {E}}_{6}$) și hiperbolic pentru n=7)
• det(F_n=[3,4,3^n-3]) = 5-n (Finit pentru F₃(=B₃) – F₄, afin pentru F₅ (${\tilde {F}}_{4}$) și hiperbolic pentru F₆)
• det(G_n=[6,3^n-2]) = 3-n (Finit pentru G₂, afin pentru G₃ (${\tilde {G}}_{2}$) și hiperbolic pentru G₄)

Serii extinse mai mici

Finite	$A_{2}$	$C_{2}$	$G_{2}$	$A_{3}$	$B_{3}$	$C_{3}$	$H_{4}$
Ordin n	[3[3],3n-3]	[4,4,3n-3]	Gn=[6,3n-2]	[3[4],3n-4]	[4,31,n-3]	[4,3,4,3n-4]	Hn=[5,3n-2]
2	[3] A2	[4] C2	[6] G2		[2] A12	[4] C2	[5] H2
3	[3[3]] A2+=${\tilde {A}}_{2}$	[4,4] C2+=${\tilde {C}}_{2}$	[6,3] G2+=${\tilde {G}}_{2}$	[3,3]=A3	[4,3] B3	[4,3] C3	[5,3] H3
4	[3[3],3] A2++=${\overline {P}}_{3}$	[4,4,3] C2++=${\overline {R}}_{3}$	[6,3,3] G2++=${\overline {V}}_{3}$	[3[4]] A3+=${\tilde {A}}_{3}$	[4,31,1] B3+=${\tilde {B}}_{3}$	[4,3,4] C3+=${\tilde {C}}_{3}$	[5,3,3] H4
5	[3[3],3,3] A2+++	[4,4,3,3] C2+++	[6,3,3,3] G2+++	[3[4],3] A3++=${\overline {P}}_{4}$	[4,32,1] B3++=${\overline {S}}_{4}$	[4,3,4,3] C3++=${\overline {R}}_{4}$	[5,33] H5=${\overline {H}}_{4}$
6				[3[4],3,3] A3+++	[4,33,1] B3+++	[4,3,4,3,3] C3+++	[5,34] H6
Det(Mn)	3(3-n)	2(3-n)	3-n	4(4-n)	2(4-n)

Serii extinse mijlocii

Finite	$A_{4}$	$B_{4}$	$C_{4}$	$D_{4}$	$F_{4}$	$A_{5}$	$B_{5}$	$D_{5}$
Odin n	[3[5],3n-5]	[4,3,3n-4,1]	[4,3,3,4,3n-5]	[3n-4,1,1,1]	[3,4,3n-3]	[3[6],3n-6]	[4,3,3,3n-5,1]	[31,1,3,3n-5,1]
3		[4,3−1,1] B2A1	[4,3] B3	[3−1,1,1,1] A13	[3,4] B3		[4,3,3] C3
4	[33] A4	[4,3,3] B4	[4,3,3] C4	[30,1,1,1] D4	[3,4,3] F4		[4,3,3,3−1,1] B3A1	[31,1,3,3−1,1] A3A1
5	[3[5]] A4+=${\tilde {A}}_{4}$	[4,3,31,1] B4+=${\tilde {B}}_{4}$	[4,3,3,4] C4+=${\tilde {C}}_{4}$	[31,1,1,1] D4+=${\tilde {D}}_{4}$	[3,4,3,3] F4+=${\tilde {F}}_{4}$	[34] A5	[4,3,3,3,3] B5	[31,1,3,3] D5
6	[3[5],3] A4++=${\overline {P}}_{5}$	[4,3,32,1] B4++=${\overline {S}}_{5}$	[4,3,3,4,3] C4++=${\overline {R}}_{5}$	[32,1,1,1] D4++=${\overline {Q}}_{5}$	[3,4,33] F4++=${\overline {U}}_{5}$	[3[6]] A5+=${\tilde {A}}_{5}$	[4,3,3,31,1] B5+=${\tilde {B}}_{5}$	[31,1,3,31,1] D5+=${\tilde {D}}_{5}$
7	[3[5],3,3] A4+++	[4,3,33,1] B4+++	[4,3,3,4,3,3] C4+++	[33,1,1,1] D4+++	[3,4,34] F4+++	[3[6],3] A5++=${\overline {P}}_{6}$	[4,3,3,32,1] B5++=${\overline {S}}_{6}$	[31,1,3,32,1] D5++=${\overline {Q}}_{6}$
8						[3[6],3,3] A5+++	[4,3,3,33,1] B5+++	[31,1,3,33,1] D5+++
Det(Mn)	5(5-n)	2(5-n)		4(5-n)	5-n	6(6-n)	4(6-n)

Unele serii extinse mai mari

Finite	$A_{6}$	$B_{6}$	$D_{6}$	$E_{6}$	$A_{7}$	$B_{7}$	$D_{7}$	$E_{7}$	$E_{8}$
Ordin n	[3[7],3n-7]	[4,33,3n-6,1]	[31,1,3,3,3n-6,1]	[3n-5,2,2]	[3[8],3n-8]	[4,34,3n-7,1]	[31,1,3,3,3,3n-7,1]	[3n-5,3,1]	En=[3n-4,2,1]
3									[3−1,2,1] E3=A2A1
4				[3−1,2,2] A22				[3−1,3,1] A3A1	[30,2,1] E4=A4
5		[4,3,3,3,3−1,1] B4A1	[31,1,3,3,3−1,1] D4A1	[30,2,2] A5				[30,3,1] A5	[31,2,1] E5=D5
6	[35] A6	[4,34] B6	[31,1,3,3,3] D6	[31,2,2] E6		[4,3,3,3,3,3−1,1] B5A1	[31,1,3,3,3,3−1,1] D5A1	[31,3,1] D6	[32,2,1] E6 *
7	[3[7]] A6+=${\tilde {A}}_{6}$	[4,33,31,1] B6+=${\tilde {B}}_{6}$	[31,1,3,3,31,1] D6+=${\tilde {D}}_{6}$	[32,2,2] E6+=${\tilde {E}}_{6}$	[36] A7	[4,35] B7	[31,1,3,3,3,30,1] D7	[32,3,1] E7 *	[33,2,1] E7 *
8	[3[7],3] A6++=${\overline {P}}_{7}$	[4,33,32,1] B6++=${\overline {S}}_{7}$	[31,1,3,3,32,1] D6++=${\overline {Q}}_{7}$	[33,2,2] E6++=${\overline {T}}_{7}$	[3[8]] A7+=${\tilde {A}}_{7}$ *	[4,34,31,1] B7+=${\tilde {B}}_{7}$ *	[31,1,3,3,3,31,1] D7+=${\tilde {D}}_{7}$ *	[33,3,1] E7+=${\tilde {E}}_{7}$ *	[34,2,1] E8 *
9	[3[7],3,3] A6+++	[4,33,33,1] B6+++	[31,1,3,3,33,1] D6+++	[34,2,2] E6+++	[3[8],3] A7++=${\overline {P}}_{8}$ *	[4,34,32,1] B7++=${\overline {S}}_{8}$ *	[31,1,3,3,3,32,1] D7++=${\overline {Q}}_{8}$ *	[34,3,1] E7++=${\overline {T}}_{8}$ *	[35,2,1] E9=E8+=${\tilde {E}}_{8}$ *
10					[3[8],3,3] A7+++ *	[4,34,33,1] B7+++ *	[31,1,3,3,3,33,1] D7+++ *	[35,3,1] E7+++ *	[36,2,1] E10=E8++=${\overline {T}}_{9}$ *
11									[37,2,1] E11=E8+++ *
Det(Mn)	7(7-n)	2(7-n)	4(7-n)	3(7-n)	8(8-n)	2(8-n)	4(8-n)	2(8-n)	9-n

Plieri geometrice

Plieri finite și afine

φA : AΓ --> AΓ' Pentru tipuri finite
Γ	Γ'	Descrierea plierii	Diagramăe Coxeter–Dynkin
I2(h)	Γ(h)	Pliere diedrică
Bn	A2n	(I,sn)
	Dn+1, A2n-1	(A3,+/-ε)
F4	E6	(A3,±ε)
H4	E8	(A4,±ε)
H3	D6
H2	A4
G2	A5	(A5,±ε)
	D4	(D4,±ε)
φ: AΓ+ --> AΓ'+ pentru tipuri afine
${\tilde {A}}_{n-1}$	${\tilde {A}}_{kn-1}$	Banale local
${\tilde {B}}_{n}$	${\tilde {D}}_{2n+1}$	(I,sn)
	${\tilde {D}}_{n+1}$, ${\tilde {D}}_{2n}$	(A3,±ε)
${\tilde {C}}_{n}$	${\tilde {B}}_{n+1}$, ${\tilde {C}}_{2n}$	(A3,±ε)
	${\tilde {C}}_{2n+1}$	(I,sn)
${\tilde {C}}_{n}$	${\tilde {A}}_{2n+1}$	(I,sn) & (I,s0)
	${\tilde {A}}_{2n}$	(A3,ε) & (I,s0)
	${\tilde {A}}_{2n-1}$	(A3,ε) & (A3,ε')
${\tilde {C}}_{n}$	${\tilde {D}}_{n+2}$	(A3,-ε) & (A3,-ε')
${\tilde {C}}_{2}$	${\tilde {D}}_{5}$	(I,s1)
${\tilde {F}}_{4}$	${\tilde {E}}_{6}$, ${\tilde {E}}_{7}$	(A3,±ε)
${\tilde {G}}_{2}$	${\tilde {D}}_{6}$, ${\tilde {E}}_{7}$	(A5,±ε)
	${\tilde {B}}_{3}$, ${\tilde {F}}_{4}$	(B3,±ε)
	${\tilde {D}}_{4}$, ${\tilde {E}}_{6}$	(D4,±ε)

O diagramă Coxeter–Dynkin (simplu înlănțuită, finită, afină sau hiperbolică) care are o simetrie (care îndeplinește o condiție, mai jos) poate fi citată prin simetrie, rezultând o nouă diagramă, în general multiplu înlănțuită prin procesul numit „pliere”.

De exemplu, în plierea D₄ la G₂, muchia din G₂ trece din clasa celor 3 noduri exterioare (valența 1), la clasa nodului central (valența 3). Și E₈ se pliază în 2 copii ale lui H₄, a doua copie scalată cu φ.

Geometric, aceasta corespunde proiecțiilor ortogonale ale politopurilor uniforme și teselărilor. În special, orice diagramă Coxeter–Dynkin finită simplu înlănțuită poate fi pliată la I₂(h), unde h este numărul Coxeter, care corespunde geometric la o proiecție pe planul Coxeter.

Câteva plieri hiperbolice

Reflexii complexe

Diagramele Coxeter–Dynkin au fost extinse la spațiul complex, Cⁿ unde nodurile sunt reflexii unitare cu perioadă mai mare de 2. Nodurile sunt etichetate cu un indice, fiind presupus 2 pentru o reflexie reală obișnuită dacă este suprimat. Coxeter descrie grupul complex, p[q]r, cu diagrama .

Un politop complex regulat 1-dimensional din $\mathbb {C} ^{1}$ este descris prin , având p vârfuri. Reprezentarea sa reală este un poligon regulat, {p}. Simetria sa este _p[] sau , de ordinul p. Un operator unitate generator pentru este văzut ca o rotație în $\mathbb {R} ^{2}$ cu 2π/p radiani în sens trigonometric, iar o latură este creată printr-o aplicare secvențială a unei singure reflexii unitare. un generator de reflexie unitară pentru un 1-politop cu p vârfuri este e^2πi/p = cos(2π/p) + i sin(2π/p). Când p = 2, generatorul este e^πi = –1, același cu reflexia punctului din planul real.

Într-un politop superior, _p{} sau reprezintă un element p-față, cu o 2-față, {} sau , reprezintă o latură reală obișnuită între două vârfuri.

1-politopuri complexe regulate

1-politopuri complexe, , reprezentați în planul Argand ca poligoane regulate pentru p = 2, 3, 4, 5 și 6, cu vârfuri negre. Centrul vârfurilor p este colorat roșu. Laturile poligoanelor reprezintă o aplicație a generatorului de simetrie, aplicând fiecare vârf la următoarea copie în sens trigonometric. Aceste laturi poligonale nu sunt elemente de margine ale politopului, întrucât un 1-politop complex nu poate avea laturi (adesea el „este” o margine complexă) și conține doar elementele vârfuri.

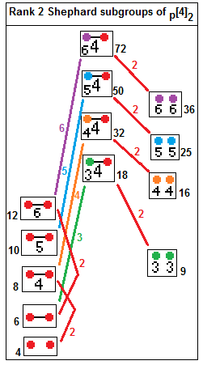
12 grupuri Shephard ireductibile cu relațiile cu subgrupurile lor indexate (cu indici). Subgrupurile cu indicele 2 se obțin prin eliminarea unei reflexii reale: p[2q]2 --> p[q]p, indice 2. p[4]q --> p[q]p, indice q.

p[4]2 subgrupuri: p=2,3,4... p[4]2 --> [p], indice p p[4]2 --> p[]×p[], indice 2

Poligoanele complexe regulate din $\mathbb {C} ^{2}$, au forma _p{q}_r sau diagrama Coxeter . Grupul de simetrie al unui poligon complex regulat nu se numește grup Coxeter, ci grup Shephard, un tip de grup de reflexie complex. ordinul _p[q]_r este $8/q\cdot (1/p+2/q+1/r-1)^{-2}$.

Grupurile Shephard de ordinul 2 sunt: ₂[q]₂, _p[4]₂, ₃[3]₃, ₃[6]₂, ₃[4]₃, ₄[3]₄, ₃[8]₂, ₄[6]₂, ₄[4]₃, ₃[5]₃, ₅[3]₅, ₃[10]₂, ₅[6]₂ și ₅[4]₃ sau , , , , , , , , , , , , , de ordinul 2q, 2p², 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 și respectiv 1800.

Grupul de simetrie _p1[q]_p2 este reprezentat prin 2 generatoare R₁, R₂, unde: R₁^p₁ = R₂^p₂ = I. Dacă q este par, (R₂R₁)^q/2 = (R₁R₂)^q/2. Dacă q este impar, (R₂R₁)^(q-1)/2R₂ = (R₁R₂)^(q-1)/2R₁. Când q este impar, p₁=p₂.

Grupul $\mathbb {C} ^{3}$ sau [1 1 1]^p este definit de 3 perioade de 2 reflexii unitare {R₁, R₂, R₃}: R₁² = R₁² = R₃² = (R₁R₂)³ = (R₂R₃)³ = (R₃R₁)³ = (R₁R₂R₃R₁)^p = 1. Perioada p poate fi văzută ca o rotație dublă în spațiul real $\mathbb {R} ^{4}$.

Un grup similar $\mathbb {C} ^{3}$ sau [1 1 1]^(p) este definit de 3 perioade de 2 reflexii unitare {R₁, R₂, R₃}: R₁² = R₁² = R₃² = (R₁R₂)³ = (R₂R₃)³ = (R₃R₁)³ = (R₁R₂R₃R₂)^p = 1.

Bibliografie

• en James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
• en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6 [2], Googlebooks [3]
  • en (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
• en Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN: 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
• en Coxeter, Regular Polytopes (1963), Macmillan Company
  • en Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN: 0-486-61480-8 (Chapter 5: The Kaleidoscope, and Section 11.3 Representation by graphs)
• en H.S.M. Coxeter and W. O. J. Moser. Generators and Relations for Discrete Groups 4th ed, Springer-Verlag. New York. 1980
• en Norman W. Johnson, Geometries and Transformations, Chapters 11,12,13, preprint 2011
• en N.W. Johnson, Ruth Kellerhals, J.G. Ratcliffe, S.T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups 1999, Volume 4, Issue 4, pp 329–353 [4] [5]
• en Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups Arhivat în 26 martie 2023, la Wayback Machine. PDF Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336

Legături externe

Materiale media legate de diagramă Coxeter–Dynkin la Wikimedia Commons

• en Eric W. Weisstein, Coxeter–Dynkin diagram la MathWorld.
• en October 1978 discussion on the history of the Coxeter diagrams de Coxeter și Dynkin în Toronto, Canada; Eugene Dynkin Collection of Mathematics Interviews, Cornell University Library.