Rombidodecadodecaedru

Rombidodecadodecaedru
(model 3D)
Descriere
Tip	poliedru uniform neconvex
Fețe	54 (30 pătrate,       12 pentagoane,       12 pentagrame)
Laturi (muchii)	120
Vârfuri	60
χ	−6
Configurația vârfului	4.5/2.4.5
Simbol Wythoff	5/2 5 | 2
Diagramă Coxeter
Grup de simetrie	Ih, [5,3], (*532)
Volum	≈42,485 a3   (a = latura)
Poliedru dual	hexacontaedru romboidal medial
Proprietăți	uniform, neconvex
Figura vârfului

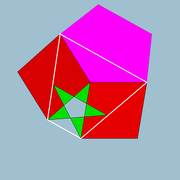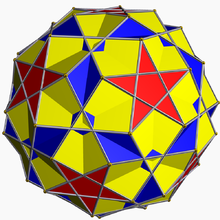
În geometrie rombidodecadodecaedrul este un poliedru stelat uniform, cu indicele U₃₈. Are 54 de fețe (30 de pătrate, 12 pentagoane și 12 pentagrame), 120 de laturi și 60 de vârfuri. Având 54 de fețe, este un pentacontatetraedru.

Este reprezentat prin diagrama Coxeter–Dynkin . Un poliedru neconvex are fețe care se intersectează care nu reprezintă muchii sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.

Are simbolul Wythoff 5/2 5 | 2 și simbolul Schläfli t_0,2{5/2,5}, iar ținând cont de construcția Wythoff acest poliedru poate fi, numit și marele dodecaedru cantelat.

Mărimi asociate

Coordonate carteziene

Coordonatele carteziene ale vârfurilor unui rombidodeacadodecaedru centrat în origine, cu lungimea laturii de 2, sunt toate permutările ale:

$\left(\,\pm (2\varphi -1),\,\pm 1,\,\pm 1\,\right)$

plus permutările pare ale

$\left(\,0,\,\pm (\varphi +1),\,\pm (2-\varphi ),\right)$

$\left(\,\pm 2,\,\pm (\varphi -1),\,\pm \varphi \,\right)$

unde $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ este secțiunea de aur.

Raza sferei circumscrise

Raza sferei circumscrise este distanța comună a vârfurilor față de origine, și anume ${\sqrt {7}}$ pentru lungimea laturii egală cu 2. Pentru lungimea laturii a, această valoare devine:

$R={\frac {\sqrt {7}}{2}}\,a\approx 1,322876\,a.$

Volum

Următoarea formulă pentru volum V este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

$V=19{\sqrt {5}}\,a\approx 42,485292\,a.$

Poliedre înrudite

Are în comun aranjamentul vârfurilor cu compusul de zece prisme triunghiulare și compusul de douăzeci de prisme triunghiulare. În plus, are în comun aranjamentul laturilor cu icosidodecadodecaedrul (având în comun fețele pentagonale și cele pentagramice) și cu rombicosaedrul (având în comun fețele pătrate).

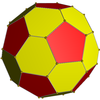Anvelopa convexă	Rombidodecadodecaedru	Icosidodecadodecaedru
Rombicosaedru	Compus de zece prisme triunghiulare	Compus de douăzeci de prisme triunghiulare

Dual: hexacontaedru romboidal medial

Poliedru dual

Dualul său este hexacontaedrul romboidal medial.

Legături externe

• en Uniform polyhedra and duals

• en Klitzing, Richard. „3D uniform polyhedra”.  Cheie: raded