Notația Coxeter
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
C1v |
C2v |
C3v |
C4v |
C5v |
C6v |
|---|---|---|---|---|---|
 Ordin 2 |
 Ordin 4 |
 Ordin 6 |
 Ordin 8 |
 Ordin 10 |
 Ordin 12 |
[2]=[2,1] D1h |
[2,2] D2h |
[2,3] D3h |
[2,4] D4h |
[2,5] D5h |
[2,6] D6h |
 Ordin 4 |
 Ordin 8 |
 Ordin 12 |
 Ordin 16 |
 Ordin 20 |
 Ordin 24 |
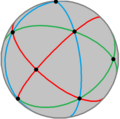 Ordin 24 |
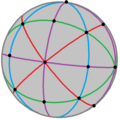 Ordin 48 |
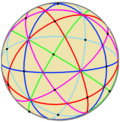 Ordin 120 | |||
| Notația Coxeter prezintă grupurile Coxeter ca o listă ordonată de ramuri ale unei diagrame Coxeter, cum ar fi grupurile poliedrice, | |||||
În geometrie notația Coxeter (sau simbol Coxeter) este un sistem de clasificare al grupurilor de simetrie, care descrie unghiurile dintre reflexiile fundamentale ale unui grup Coxeter într-o notație între paranteze care exprimă structura unei diagrame Coxeter–Dynkin, cu modificatori pentru a indica anumite subgrupuri. Notația este numită după H.S.M. Coxeter și a fost definită mai cuprinzător de Norman Johnson.
Grupuri de reflexie[modificare | modificare sursă]
La grupurile Coxeter, definite prin reflexii pure, există o corespondență directă între notația cu paranteze și diagrama Coxeter–Dynkin. Numerele din notația cu paranteze drepte reprezintă ordinea reflexiilor în oglindă în ramurile diagramei Coxeter. Folosește aceeași simplificare, suprimând 2s între planele de oglindire ortogonale.
Notația Coxeter este simplificată prin exponenți care reprezentă numărul de ramuri într-un rând pentru diagrama liniară.Grupul An este reprezentat de [3n−1], pentru a descrie n noduri conectate prin n−1 ramuri de ordinul 3. Exemplul A2 = [3,3] = [32], respectiv [31,1] reprezintă diagramele ![]()
![]()
![]()
![]()
![]() , respectiv
, respectiv ![]()
![]()
![]() .
.
Inițial Coxeter a reprezentat diagramele bifurcate prin poziționarea verticală a numerelor, dar ulterior notația a fost abreviată la una cu exponenți, cum ar fi [...,3p,q] sau [3p,q,r], începând cu [31,1,1] sau [3,31,1] = ![]()
![]()
![]()
![]() sau
sau ![]()
![]()
![]() pentru D4. Coxeter admite zerourile drept cazuri particulare pentru a se potrivi cu familia An, de exemplu A3 = [3,3,3,3] = [34,0,0] = [34,0] = [33,1] = [32,2], drept
pentru D4. Coxeter admite zerourile drept cazuri particulare pentru a se potrivi cu familia An, de exemplu A3 = [3,3,3,3] = [34,0,0] = [34,0] = [33,1] = [32,2], drept ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() .
.
Grupurile Coxeter formate din diagrame ciclice sunt reprezentate prin paranteze rotunde între parantezele drepte, cum ar fi [(p,q,r)] = ![]() pentru grupul triunghiului(d) (p q r). Dacă ordinele ramurilor sunt egale, ele pot fi grupate printr-un exponent între paranteze drepte, care indică lungimea ciclului, de exemplu [(3,3,3,3)] = [3[4]], reprezentând diagramele Coxeter
pentru grupul triunghiului(d) (p q r). Dacă ordinele ramurilor sunt egale, ele pot fi grupate printr-un exponent între paranteze drepte, care indică lungimea ciclului, de exemplu [(3,3,3,3)] = [3[4]], reprezentând diagramele Coxeter ![]()
![]()
![]()
![]()
![]() sau
sau ![]()
![]()
![]() .
. ![]()
![]()
![]()
![]()
![]() poate fi reprezentată prin [3,(3,3,3)] sau [3,3[3]].
poate fi reprezentată prin [3,(3,3,3)] sau [3,3[3]].
Diagramele în buclă mai complicate pot fi și ele exprimate, dar cu grijă. Grupul Coxeter paracompact ![]()
![]()
![]()
![]()
![]() poate fi reprezentat prin notația Coxeter [(3,3,(3),3,3)], cu paranteze imbricate, având două bucle [(3,3,3)] adiacente și care poate fi reprezentat mai compact prin [3[ ]×[ ]], reprezentând simetria rombică a diagramei Coxeter. Graful complet al diagramei paracompacte
poate fi reprezentat prin notația Coxeter [(3,3,(3),3,3)], cu paranteze imbricate, având două bucle [(3,3,3)] adiacente și care poate fi reprezentat mai compact prin [3[ ]×[ ]], reprezentând simetria rombică a diagramei Coxeter. Graful complet al diagramei paracompacte ![]() sau
sau ![]()
![]()
![]() este reprezentat ca [3[3,3]] cu exponentul [3,3] pentru simetria diagramei sale Coxeter a tetraedrului regulat.
este reprezentat ca [3[3,3]] cu exponentul [3,3] pentru simetria diagramei sale Coxeter a tetraedrului regulat.
De obicei în diagrama Coxeter ramurile de ordinul 2 nu sunt trasate, dar notația cu paranteze are un 2 explicit pentru a conecta subgrafurile. Deci diagrama Coxeter ![]()
![]()
![]()
![]()
![]()
![]()
![]() = A2×A2 = 2A2 poate fi reprezentat prin [3]×[3] = [3]2 = [3,2,3]. Uneori ramurile explicite de ordinul 2 pot fi descrise fie cu o etichetă 2, fie cu o linie cu un interval:
= A2×A2 = 2A2 poate fi reprezentat prin [3]×[3] = [3]2 = [3,2,3]. Uneori ramurile explicite de ordinul 2 pot fi descrise fie cu o etichetă 2, fie cu o linie cu un interval: ![]()
![]()
![]()
![]()
![]()
![]()
![]() sau
sau ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , ca o prezentare identică cu [3,2,3].
, ca o prezentare identică cu [3,2,3].
|
|
|
Pentru grupurile afine și hiperbolice, indicele este cu unul mai mic decât numărul de noduri în fiecare caz, deoarece fiecare dintre aceste grupuri a fost obținut prin adăugarea unui nod la diagrama unui grup finit.
Există numeroase extensii ale notației Coxeter, folosite pentru subgrupuri.
Bibliografie[modificare | modificare sursă]
- en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6 [1]
- (Paper 22) Coxeter, H.S.M. (), „Regular and Semi Regular Polytopes I”, Math. Z., 46: 380–407, doi:10.1007/bf01181449
- (Paper 23) Coxeter, H.S.M. (), „Regular and Semi-Regular Polytopes II”, Math. Z., 188 (4): 559–591, doi:10.1007/bf01161657
- (Paper 24) Coxeter, H.S.M. (), „Regular and Semi-Regular Polytopes III”, Math. Z., 200: 3–45, doi:10.1007/bf01161745
- en Coxeter, H.S.M.; Moser, W.O.J. (). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.
- en Norman Johnson Uniform Polytopes, Manuscript (1991)
- en Norman Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- en Norman Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups Arhivat în , la Wayback Machine. PDF Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336
- en Norman Johnson: Geometries and Transformations, (2018) ISBN: 978-1-107-10340-5 Chapter 11: Finite symmetry groups [2]
- en Conway, John Horton; Delgado Friedrichs, Olaf; Huson, Daniel H.; Thurston, William P. (), „On three-dimensional space groups”, Beiträge zur Algebra und Geometrie, 42 (2): 475–507, ISSN 0138-4821, MR 1865535
- en John H. Conway and Derek A. Smith, On Quaternions and Octonions, 2003, ISBN: 978-1-56881-134-5
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008), The Symmetries of Things, ISBN: 978-1-56881-220-5 Ch.22 35 prime space groups, ch.25 184 composite space groups, ch.26 Higher still, 4D point groups



































