Antiprismă pătrată snub
| Antiprismă pătrată snub | |
 | |
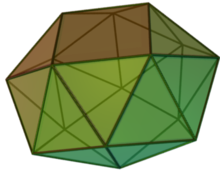| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J84 – J85 – J86 |
| Fețe | 26 (2 pătrate, 24 triunghiuri) |
| Laturi (muchii) | 40 |
| Vârfuri | 16 |
| χ | 2 |
| Configurația vârfului | 8 (35), 8 (34.4) |
| Grup de simetrie | D4d, [24,8], (2*4), ordin 16 |
| Arie | ≈ 12,392 a2 (a = latura) |
| Volum | ≈ 3,601 a3 (a = latura) |
| Proprietăți | convexă |
| Desfășurată | |
 | |
În geometrie antiprisma pătrată snub este unul dintre poliedrele Johnson (J85).
Este unul dintre poliedrele elementare Johnson care nu se pot obține prin „tăiere și lipire” ale poliedrelor platonice sau arhimedice, deși este înrudit cu icosaedrul, care are aceeași simetrie, dar de patru ori în loc de trei.
Construcție
[modificare | modificare sursă]Antiprisma pătrată snub este construită așa cum sugerează numele, dintr-o antiprismă pătrată asopra căreia se aplică operația snub. Este reprezentată prin simbolul ss{2,8}, simbolul s{2,8} fiind cel al antiprismei pătrate.[1] În notația Conway a poliedrelor poate fi construită ca sY4 (piramidă pătrată snub).[2]
De asemenea, poate fi construită ca o girobianticupolă, conectând două anticupole cu orientări girate.
Mărimi asociate
[modificare | modificare sursă]Coordonate carteziene
[modificare | modificare sursă]Fie k ≈ 0,82354 rădăcina pozitivă a polinomului de gradul al treilea
și h ≈ 1,35374 definit ca
Atunci coordonatele carteziene ale unei antiprisme pătrate snub cu lungimea laturii de 2 sunt date de reuniunea orbitelor punctelor
sub acțiunea grupului generat de o rotație în jurul axei z cu 90° și printr-o rotație de 180° în jurul unei drepte perpendiculare pe axa z și făcând un unghi de 22,5° cu axa x.[3]
Arie și volum
[modificare | modificare sursă]Aria suprafeței antiprismei pătrate snub cu latura a este[4]
iar volumul său este
unde ξ ≈ 3,60122 este cea mai mare rădăcină reală a polinomului[5]
Antiprisme snub
[modificare | modificare sursă]Construită similar, ss{2,6} este o antiprismă triunghiulară snub (un octaedru cu simetrie inferioară) și rezultatul este un icosaedru regulat. O „antiprismă pentagonală snub”, ss{2,10} sau n-antiprisme din dimensiuni superioare pot fi construite similar, dar nu ca un poliedru convex cu triunghiuri echilaterale. Poliedrul Johnson precedent, bisfenoidul snub, poate fi construit și el ca ss{2,4}, dar trebuie reținut că în antiprisma diagonală există două fețe digonale degenerate (desenate cu roșu).
| Simetrie | D2d, [2+,4], (2*2) | D3d, [2+,6], (2*3) | D4d, [2+,8], (2*4) | D5d, [2+,10], (2*5) |
|---|---|---|---|---|
| Antiprisme |  s{2,4} A2     (v:4; e:8; f:6) |
 s{2,6} A3  (v:6; e:12; f:8) |
 s{2,8} A4  (v:8; e:16; f:10) |
 s{2,10} A5  (v:10; e:20; f:12) |
| Antiprisme trunchiate |
 ts{2,4} tA2 (v:16;e:24;f:10) |
 ts{2,6} tA3 (v:24; e:36; f:14) |
 ts{2,8} tA4 (v:32; e:48; f:18) |
 ts{2,10} tA5 (v:40; e:60; f:22) |
| Simetrie | D2, [2,2]+, (222) | D3, [3,2]+, (322) | D4, [4,2]+, (422) | D5, [5,2]+, (522) |
| Antiprisme snub |
J84 | Icosaedru | J85 | Concavă |
| sY3 = HtA3 | sY4 = HtA4 | sY5 = HtA5 | ||
 ss{2,4} (v:8; e:20; f:14) |
 ss{2,6} (v:12; e:30; f:20) |
 ss{2,8} (v:16; e:40; f:26) |
 ss{2,10} (v:20; e:50; f:32) |
Note
[modificare | modificare sursă]- ^ en Snub Anti-Prisms
- ^ en „PolyHédronisme”.
- ^ en Timofeenko, A. V. (). „The non-Platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Science. 162 (5): 725. doi:10.1007/s10958-009-9655-0.
- ^ en Wolfram Research, Inc. (). „Wolfram|Alpha Knowledgebase”. Champaign, IL.
PolyhedronData[{"Johnson", 85}, "SurfaceArea"] - ^ en Wolfram Research, Inc. (). „Wolfram|Alpha Knowledgebase”. Champaign, IL.
MinimalPolynomial[PolyhedronData[{"Johnson", 85}, "Volume"], x]
Legături externe
[modificare | modificare sursă]
Materiale media legate de antiprismă pătrată snub la Wikimedia Commons- en Eric W. Weisstein, Snub square antiprism la MathWorld.
- en Eric W. Weisstein, Johnson solid la MathWorld.
