Triunghi
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. |
| Triunghi | |
 Imagine | |
| Laturi și vârfuri | 3 |
|---|---|
| Simbol Schläfli | {3} (pt. echilateral) |
| Diagramă Coxeter | |
| Grup de simetrie | Dih3 [3], 2*3 |
| Arie | diverse metode |
| Unghi interior (grade) | 60° (pt. echilateral) |
| Proprietăți | convex |
Triunghiul este figura geometrică dată de reuniunea segmentelor închise determinate de trei puncte distincte necoliniare. Este una dintre formele poligonale fundamentale ale geometriei.
Definiții
- punctele A, B, C se numesc vârfurile triunghiului.
- [AB], [BC], [AC] se numesc laturile triunghiului.
- se numesc unghiurile (interne) triunghiului.
Clasificare
Clasificarea triunghiurilor se face:
- în funcție de lungimile laturilor
- după felul unghiurilor
În funcție de lungimile laturilor
Un triunghi cu toate laturile congruente se numește triunghi echilateral. Un triunghi cu două laturi congruente se numește triunghi isoscel. Un triunghi care are laturile de lungimi diferite se numește triunghi scalen (sau oarecare).
-
Triunghi echilateral
-
Triunghi isoscel
-
Triunghi scalen
După felul unghiurilor
Triunghiul cu toate unghiurile ascuțite este numit triunghi ascuțitunghic. Dacă unul dintre unghiuri este drept, triunghiul este denumit dreptunghic. Triunghiul cu un unghi mai mare de 900 se numește triunghi obtuzunghic.
-
Triunghi dreptunghic.
-
Triunghi obtuzunghic.
-
Triunghi ascuțitunghic.
Drepte, segmente și puncte remarcabile

Bisectoarea
Bisectoarea este semidreapta interioară, cu originea în vârful unghiului, care împarte unghiul în 2 unghiuri congruente. Bisectoarele celor trei unghiuri interne ale triunghiului se numesc bisectoarele interne ale triunghiului.
Înălțimea
Înălțimea este segmentul de dreaptă determinat de un vârf al unui triunghi și piciorul perpendicularei duse din acel vârf pe latura opusă sau pe prelungirea ei.
Mediana
Mediana este segmentul de dreaptă care unește un vârf al unui triunghi cu mijlocul laturii opuse.
Mediatoarea
Mediatoarea este dreapta perpendiculară pe un segment dusă prin mijlocul acestuia. Mediatoarele celor trei laturi ale triunghiului se numesc mediatoarele triunghiului.
Linia mijlocie
Linia mijlocie este segmentul determinat de mijloacele a două laturi ale triunghiului. Ea este paralelă cu cea de-a treia latură și este egală cu jumătate din lungimea acesteia. Cele trei linii mijlocii ale unui triunghi formează un triunghi asemenea cu triunghiul inițial.
Centrul cercului circumscris
Centrul cercului circumscris unui triunghi se află la intersecția celor trei mediatoare (perpendiculare pe mijlocul fiecărei laturi) ale triunghiului respectiv. Centrul cercului circumscris se află în interiorul triunghiului (în cazul triunghiurilor ascuțitunghice) sau în exteriorul triunghiului (în cazul triunghiurilor obtuzunghice). La triunghiurile dreptunghice centrul cercului circumscris se găsește pe ipotenuză, la mijlocul acesteia.
Centrul cercului înscris
Centrul cercului înscris într-un triunghi se află la intersecția celor trei bisectoare ale unghiurilor interne ale triunghiului.
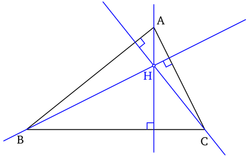
Ortocentrul
Ortocentrul unui triunghi se află la intersecția celor trei înălțimi ale triunghiului respectiv. Ortocentrul se află în interiorul triunghiului (în cazul triunghiurilor ascuțitunghice) sau în exteriorul triunghiului (în cazul triunghiurilor obtuzunghice). La triunghiurile dreptunghice ortocentrul este chiar vârful unghiului drept.
Centrul de greutate
Intersecția celor trei mediane ale triunghiului este „centrul de greutate” al triunghiului.
Ortocentrul, centrul de greutate și centrul cercului circumscris triunghiului sunt coliniare, formând dreapta lui Euler.
Centrul de greutate se află pe fiecare mediană la o distanță de 2/3 de la vârf și de 1/3 de la bază.
Congruență
Două triunghiuri sunt congruente dacă laturile și unghiurile corespunzătoare sunt congruente.
Criterii de congruență
Criteriile de congruență sunt teoreme care permit verificarea congruenței a două triunghiuri folosind numai trei congruențe între elementele lor.[1]
- Criteriul U.L.U. (unghi-latură-unghi): Dacă o latură și unghiurile alăturate ei dintr-un triunghi sunt congruente cu elementele corespunzătoare lor din alt triunghi, atunci cele două triunghiuri sunt congruente.
- Criteriul L.U.L. (latură-unghi-latură): Dacă două laturi și unghiul determinat de ele dintr-un triunghi sunt congruente cu elementele corespunzătoare din alt triunghi, atunci cele 2 triunghiuri sunt congruente.
- Criteriul L.L.L. (latură-latură-latură): Dacă cele trei laturi dintr-un triunghi sunt congruente cu laturile corespunzătoare lor din alt triunghi, atunci cele două triunghiuri sunt congruente.
Congruența triunghiurilor dreptunghice
- Cazul C.C. (catetă-catetă): două triunghiuri dreptunghice care au catetele congruente, sunt congruente.
- Cazul C.U. (catetă-unghi): două triunghiuri dreptunghice care au câte o catetă și câte un unghi ascuțit congruent,sunt congruente.
- Cazul I.U. (ipotenuză-unghi): două triunghiuri dreptunghice care au ipotenuzele congruente și o pereche de unghiuri ascuțite congruente, sunt congruente.
- Cazul I.C. (ipotenuză-catetă): două triunghiuri dreptunghice care au ipotenuzele congruente și o pereche de catete congruente, sunt congruente.
Asemănare
Două triunghiuri sunt asemenea dacă au unghiurile corespunzătoare congruente și laturile corespunzătoare proporționale.
Criterii de asemănare
Criteriile de asemănare sunt teoreme care permit verificarea asemănării a două triunghiuri.[2]
- Criteriul U.U. (unghi-unghi): Două triunghiuri sunt asemenea dacă au câte două unghiuri respectiv congruente .
- Criteriul L.U.L. (latură-unghi-latura): Dacă două triunghiuri au două laturi proporționale și un unghi congruent, atunci triunghiurile sunt asemenea.
- Criteriul L.L.L. (latură-latură-latură): Dacă două triunghiuri au laturile corespunzătoare proporționale, atunci cele două triunghiuri sunt asemenea.
Teoreme și consecințe
- O paralelă dusă la una din laturile unui triunghi, formează cu celelalte două laturi, sau cu prelungirile lor, un triunghi asemenea cu triunghiul dat.
- Orice triunghi este asemenea cu el însuși.
- Dacă triunghiul ABC este asemenea cu triunghiul A1B1C1, iar triunghiul A1B1C1 este asemenea cu triunghiul A2B2C2, atunci și triunghiul ABC este asemenea cu triunghiul A2B2C2.
- Două triunghiuri congruente sunt întotdeauna asemenea.
- Toate triunghiurile echilaterale sunt asemenea între ele.
Reguli, proprietăți, teoreme aplicabile
- În orice triunghi suma măsurilor unghiurilor interne este de 180°.
- Un triunghi are șase unghiuri externe, congruente două câte două.
- Într-un triunghi isoscel unghiurile alăturate bazei sunt congruente.
- Într-un triunghi dreptunghic unghiurile ascuțite sunt complementare.
- Într-un triunghi dreptunghic lungimea ipotenuzei este mai mare decât oricare din lungimile celor două catete.
- Într-un triunghi oarecare, laturii mai mari i se opune un unghi mai mare decât cel care se opune laturii mai mici.
- Într-un triunghi ascuțitunghic centrul cercului circumscris se găsește în interiorul triunghiului.
- Într-un triunghi obtuzunghic centrul cercului circumscris se găsește în exteriorul triunghiului.
- Într-un triunghi dreptunghic centrul cercului circumscris coincide cu mijlocul ipotenuzei.
- Cercul înscris într-un triunghi intersectează (atinge) fiecare latură într-un singur punct, numit punct de tangență.
- Într-un triunghi se pot construi trei linii mijlocii.
- Într-un triunghi linia mijlocie este paralelă cu cea de-a treia latură a triunghiului, și are lungimea egală cu jumătate din lungimea acesteia.
- Triunghiul având ca laturi cele trei linii mijlocii dintr-un triunghi se numește triunghi median.
- Ortocentrul (punctul de intersecție al celor trei înălțimi) unui triunghi ascuțitunghic se găsește în interiorul triunghiului.
- Ortocentrul unui triunghi obtuzunghic se găsește în exteriorul triunghiului.
- Ortocentrul unui triunghi dreptunghic coincide cu vârful unghiului drept.
- Teorema lui Thales: în orice triunghi, o paralelă dusă la una din laturi împarte celelalte două laturi, sau prelungirile acestora, în segmente proporționale.
- Reciproca Teoremei lui Thales: în orice triunghi, dacă o dreaptă determină pe două laturi, sau pe prelungirile acestora, segmente proporționale, atunci ea este paralelă cu a treia latură.
- Teorema bisectoarei: bisectoarea unui unghi al unui triunghi oarecare determină pe latura opusă segmente proporționale cu laturile care formează unghiul.
- Teorema lui Pitagora: într-un triunghi dreptunghic, suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei.
- Teorema lui Pitagora generalizată: într-un triunghi oarecare, pătratul unei laturi este egal cu suma pătratelor celorlalte două laturi minus de două ori produsul lor multiplicat cu cosinusul unghiului dintre ele.[3]
- Teorema lui Ceva: într-un triunghi oarecare ABC, dacă D, E, F sunt trei puncte diferite de vârfurile triunghiului, aflate respectiv pe laturile acestuia [BC], [CA], [AB], dreptele AD, BE și CF sunt concurente dacă și numai dacă: . [4]
- Teorema lui Cesàro: într-un triunghi cu laturile a, b, c, are loc relația: , unde ma, mb și mc sunt lungimile medianelor.[5]
- Într-un triunghi oarecare, măsura unui unghi exterior triunghiului este egală cu suma măsurilor unghiurilor interioare nealăturate. Un unghi exterior unui triunghi este mai mare decât oricare din unghiurile interne nealăturate.
Formule
Perimetru și semiperimetru
Arie
- , iar
Formula lui Heron:
Alte forme ale formulei lui Heron:
Formule derivate din formula lui Heron:

- unde
- unde
- unde , iar
Alte formule
- sau
- sau
- sau
- ; ;
- ; ;
Notă. Au fost utilizate notațiile:
A (arie); l (una dintre laturile triunghiului); a, b, c (laturile unui triunghi); α,β,γ (unghiurile triunghiului); P (perimetru); p (semiperimetru); h (înălțime); R (raza cercului circumscris triunghiului); D (diametrul cercului circumscris al triunghiului) ; r (raza cercului înscris în triunghi); pr (proiecția catetei pe ipotenuză); m (mediana).
Note
- ^ Hadamard (1962), Lecții de geometrie elementară. Geometrie plană, p. 28.
- ^ Hadamard (1962), Lecții de geometrie elementară. Geometrie plană, p. 93.
- ^ fr W. Gellert, H. Küstner, M. Hellwich, H. Kästner, Petite encyclopédie des mathématiques, Édition Didier, Paris, 1980, chapitre 11-2, p. 265. ISBN 978-2-278-03526-7
- ^ Viorel Gh. Vodă (1983), Vraja geometriei demodate, p. 226.
- ^ Viorel Gh. Vodă (1983), Vraja geometriei demodate, p. 225.
Bibliografie
- Jacques Hadamard, Lecții de geometrie elementară. Geometrie plană, Editura Tehnică, București, 1962
- Viorel Gh. Vodă, Vraja geometriei demodate, Editura Albatros, București, 1983
- Dumitru Săvulescu, Ștefan Sabău, Emil Teodorescu. Breviar teoretic și teste de matematică, Editura Corint, București 2001.
Lectură suplimentară
- Traian Lalescu, Geometria triunghiului, Editura Tineretului, București, 1958.
- Ionescu-Țiu, C., Geometrie plană și în spațiu, pentru admiterea la facultate, Editura Albatros, București, 1976.
- Cătălin Barbu, Teoreme fundamentale din geometria triunghiului, Editura Unique, 2008.
Legături externe
![]() Materiale media legate de triunghi la Wikimedia Commons
Materiale media legate de triunghi la Wikimedia Commons
- en Wolfram MathWorld: Triangle, accesat la 9 octombrie 2020


![{\displaystyle [AB]\cup [BC]\cup [CA]=\triangle [ABC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b4fc29b17a8101104eb534922becd82eb4e876)




























































