Teorema lui Thales

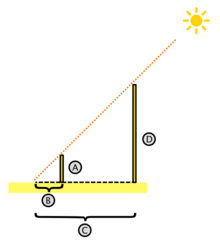
Thales din Milet (624 - 546 î.Hr.), după cum afirmă Proclus, ar fi cunoscut teoremele privitoare la triunghiurile asemenea, cu ajutorul cărora a măsurat depărtarea unui vas de la țărmul mării. De asemenea, tot cu ajutorul unor teoreme de geometrie, el ar fi măsurat înălțimea marii piramide a lui Keops.

Astăzi, sub numele de „teorema lui Thales” sunt cunoscute legăturile care există într-o configurație de cinci puncte, ABCDE, unde A, B, D sunt coliniare, A, C, E sunt coliniare, iar DE este paralel cu BC.

De aici se pot lămuri mai departe asemănarea a două triunghiuri (șase puncte) și mai departe, asemănarea a două figuri geometrice în spațiul tridimensional sau cu mai multe dimensiuni. Se poate caracteriza o geometrie prin atributul „thalesiană”, indicând că în acea geometrie funcționează teorema lui Thales.

Pentru a demonstra teorema lui Thales este necesară noțiunea de „comensurabilitate”. Cu alte cuvinte, segmentele care intervin trebuie să aibă o măsură comună, iar raportul lor trebuie să fie un număr rațional.

Cum, în general, două segmente nu sunt comensurabile, în geometria modernă apar noțiunile de „număr real”, „corp”, „spațiu vectorial”, „transformare liniară” și până la urmă „omotetie” (adică asemănare în cel mai general caz), care pot valida teorema lui Thales și pentru alte triunghiuri cu laturi incomensurabile.

Enunț[modificare | modificare sursă]

O paralelă DE la baza BC a unui triunghi ABC împarte laturile AB și AC în segmente proporționale : ${\frac {AD}{DB}}={\frac {AE}{EC}}$

Demonstrație pentru segmente comensurabile[modificare | modificare sursă]

Cazul AD = DB[modificare | modificare sursă]

În acest caz, se prelungește DE până întâlnește în M paralela dusă prin C la AB. Așadar DM || BC și MC || DB, deci DMCB este un paralelogram iar DB = MC.

Atunci: AD = DB = MC.

Rezultă că triunghiurile ADE și CME sunt egale (cazul ULU de egalitate). În concluzie, AE = EC și

AE:EC = AD:DB ( = 1 )

Linia mediană a unui trapez[modificare | modificare sursă]

În trapezul AA'BB' se duce prin A o paralelă la A'B' , care taie DE și BB' în M, respectiv N.

Se știe deja că AM = MN (DE fiind linie mijlocie și A’B’ paralela la AN). Cum AMEA' și MNB'E sunt paralelograme, rezultă: A'E = AM = MN = EB', A'E:EB' = AM:MN = AD:DB și

A'E:EB' = AD:DB

Segmente comensurabile[modificare | modificare sursă]

Fără a pierde din generalitate, să presupunem că AM:MB = 5:3. Se duc drepte paralele cu baza BB' prin punctele care reprezintă măsura comună a segmentelor AM și MB. Dreaptele paralele vor împărți A'B' de asemenea în segmente egale, pentru că fiecare trei paralele alăturate trasează un trapez și linia lui mediană. Așadar A'N:NB' este de asemenea egal cu 5:3. În concluzie,

AM:MB = A'N:NB' Q.E.D.

Limita acestui raționament e dată de existența segmentelor incomensurabile, cum ar fi de pildă 1:√2. Oricum, un astfel de raport poate fi oricât de bine aproximat prin numere raționale (adică prin segmente comensurabile)

AM:MB ≈ A'N:NB'

Demonstrația lui Euclid[modificare | modificare sursă]

Euclid face apel la raportul unor arii :

AD:DB = aria(AED):aria(DEB) = aria(ADE):aria(EDC) = AE:EC

1) Triunghiurile AED și DEB au aceeași înălțime h. Așadar raportul ariilor este egal cu raportul bazelor AD și DB.

2a) Triunghiurile BDC și BEC au aceeași arie, pentru că au aceeași înălțime, care este distanța dintre paralelele BC și DE.

2b) Atunci aria(AED):aria(DEB) = aria(ADE):aria(EDC) și care, mai departe,

3) Este egală cu raportul segmentelor AE și EC, pentru că cele două triunghiuri au aceeași înălțime h'. Q.E.D.

Deficiența demonstrației prin ”feliere” în fața demonstrației lui Euclid va fi compensată mult mai aproape de zilele noastre, prin dezvoltarea analizei matematice, care studiază însumarea unui număr tot mai mare de cantități din ce în ce mai mici. Odată clarificate noțiunile de număr real, corp și spațiu vectorial, teorema lui Thales reapare în matematica modernă sub numele de „omotetie”.

Reciproca teoremei lui Thales[modificare | modificare sursă]

Dacă o dreaptă determină pe două din laturile unui triunghi, sau pe prelungirile acestora, segmente proporționale, atunci ea este paralelă cu a treia latură a triunghiului.

Dacă:

${\frac {AD}{DB}}={\frac {AE}{EC}}$