Politop regulat
 Un pentagon regulat este un poligon, un politop bidimensional cu 5 laturi, cu simbolul Schläfli {5}. |
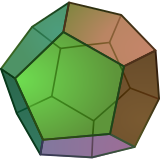 Un dodecaedru regulat este un poliedru, un politop tridimensional, cu 12 fețe pentagonale, cu simbolul Schläfli {5,3}. |
 Un 120-celule regulat este un 4-politop, un politop 4-dimensional, cu 120 de celule dodecaedrice, cu simbolul Schläfli {5,3,3}. (arătat aici ca diagramă Schlegel) |
 Un fagure cubic regulat este o teselare, un politop tridimensional infinit, cu simbolul Schläfli {4,3,4}. |
 Cele 256 de vârfuri și 1024 de laturi ale unui 8-cub pot fi prezentate în această proiecție ortogonală (poligon Petrie) | |
În matematică, un politop regulat este un politop al cărui grup de simetrie este tranzitiv față de steagurile sale, conferindu-i astfel cel mai înalt grad de simetrie. Toate elementele și j-fețele sale (pentru orice 0 ≤ j ≤ n, unde n este dimensiunea politopului) — celule, fețe etc. — sunt, de asemenea, tranzitive pe simetriile politopului și sunt politopuri regulate de dimensiune ≤ n.
Politopurile regulate sunt generalizarea în orice număr de dimensiuni ale poligoanelor regulate (de exemplu pătratul sau pentagonul regulat) și a poliedrelor regulate (de exemplu, cubul). Marea simetrie a politopurilor regulate le conferă o calitate estetică care prezintă interes atât pentru matematicieni, cât și pentru ceilalți oameni.
În mod clasic, un politop regulat în n dimensiuni poate fi definit ca având fațete regulate [(n – 1)-fețe] și figuri ale vârfului regulate. Aceste două condiții sunt suficiente pentru a se asigura că toate fețele și vârfurile sunt uniforme. Totuși, această definiție nu corespunde pentru politopuri abstracte.
Un politop regulat poate fi reprezentat printr-un simbol Schläfli de forma {a, b, c, ...., y, z}, cu fațetele regulate {a, b, c, ..., y} și figurile regulate ale vârfurilor {b, c, ..., y, z}.
Clasificare și descriere[modificare | modificare sursă]
Politopurile regulate sunt clasificate în primul rând după numărul lor de dimensiuni.
În continuare, ele pot fi clasificate în funcție de simetrie. De exemplu, cubul și octaedrul regulat au aceeași simetrie, la fel și dodecaedrul regulat cu icosaedrul. Grupurile de simetrie sunt uneori denumite după politopurile regualte, de exemplu simetriile tetraedrică și icosaedrică.
Trei clase speciale de politopuri regulate există în toate dimensiunile:
În două dimensiuni există infinit de multe poligoane regulate. În trei și patru dimensiuni există mai multe poliedre și 4-politopuri regulate în afară de cele trei menționate mai sus. În cinci și mai multe dimensiuni cele trei sunt singurele. A se vedea și lista politopurilor regulate.
Noțiunea de politop este uneori generalizată pentru a include tipuri de obiecte geometrice înrudite. Există exemple regulate ale unora dintre acestea.
Simboluri Schläfli[modificare | modificare sursă]
În secolul al XIX-lea Ludwig Schläfli a creat pentru politopurile regulate o notație simbolică concisă, care, ușor modificată, a devenit standard. Notația le descrie adăugând treptat câte o dimensiune.
- Un poligon regulat convex având n laturi este notat cu {n}. Deci un triunghi echilateral este {3}, un pătrat {4} și așa mai departe la infinit. Un poligon stelat regulat care se înfășoară de m ori în jurul centrului său este notat prin fracția {n/m}, unde n și m sunt numere coprime, deci o pentagramă regulată este notată {5/2}.
- Un poliedru regulat având {n} fețe cu p fețe incidente în jurul unui vârf este notat cu {n, p}. Cele nouă poliedre regulate sunt {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 5/2} {5/2, 3} {5, 5/2} și {5/2, 5}. {p} este figura vârfului poliedrului.
- Un 4-politop regulat având celule {n, p} din care q celule se întâlnesc în jurul unei laturi este notat cu {n, p, q}. Figura vârfului acestui 4-politop este {p, q}.
- Un 5-politop regulat este un {n, p, q, r} ș.a.m.d.
Dualitatea politopurilor regulate[modificare | modificare sursă]
Politopul dual al unui politop regulat este și el un politop regulat. Simbolul Schläfli al unui politop dual este simbolul original scris în ordine inversă: {3, 3} este autodual, {3, 4} este dualul lui {4, 3}, {4, 3, 3} este dualul lui {3, 3, 4} ș.a.m.d.
Figura vârfului unui politop regulat este dualul fațetei politopului dual. De exemplu, figura vârfului lui {3, 3, 4} este {3, 4}, al căriei dual este {4, 3} — o celulă a {4, 3, 3}.
Hipercubul și ortoplexul sunt unul dualul celuilalt în orice dimensiune.
Dacă simbolul Schläfli este palindromic, adică este la fel când este citit în ordine inversă, atunci politopul este autodual. Politopurile autoduale regulate sunt:
- Toate poligoanele regulate, {a}.
- Toate n-simplexurile regulate, {3,3,...,3}.
- 24-celule regulat în 4 dimensiuni, {3,4,3}.
- Marele 120-celule ({5,5/2,5}) și marele 120-celule stelat ({5/2,5,5/2}) în 4 dimensiuni.
- Toți fagurii cubici regulați n-dimensionali, {4,3,...,3,4}. Aceștia pot fi tratați ca politopuri infinite.
- Pavările și fagurii hiperbolici (pavări {p,p} cu p > 4 în 2 dimensiuni, {4,4,4}, {5,3,5}. {3,5,3}, {6,3,6}, și {3,6,3} în 3 dimensiuni, {5,3,3,5} în 4 dimensiuni, și {3,3,4,3,3} în 5 dimensiuni).
Simplexuri regulate[modificare | modificare sursă]

|

|

|

|
| Segment | Triunghi | Tetraedru | 5-celule |

|

|

|
Se începe cu un punct A. Se marchează punctul B la distanța r de acesta și se unesc pentru a forma un segment. Se marchează punctul C într-o a doua dimensiune, ortogonală, la distanța r de ambele și se unește cu A și B pentru a forma un triunghi echilateral'. Se marchează punctul D într-o a treia dimensiune, ortogonală, la distanța r de toate cele trei și se unesc pentru a forma un tetraedru regulat. Și așa mai departe pentru dimensiuni superioare.
Acestea sunt simplexurile regulate. Numele lor sunt, în ordinea dimensiunilor:
- 0. Punct
- 1. Segment
- 2. Triunghi echilateral (trigon regulat)
- 3. Tetraedru regulat
- 4. 5-celule regulat (4-simplex)
- 5. 5-simplex
- ... Un n-simplex are n+1 vârfuri.
Politopuri de măsură (hipercuburi)[modificare | modificare sursă]

|
|

|
| Pătrat | Cub | Tesseract |

|

|

|
Se începe cu punctul A. Se extinde spre punctul B aflat la distanța r cu un segment. Se extinde segmentul pe o lungime r într-o direcție ortogonală pe segmentul AB, de la B la C și de la A la D pentru a forma pătratul ABCD. Se extende pătratul la distanța r ortogonal pe AB și BC (de exemplu „în sus”). se marchează noile puncte E,F,G,H pentru a forma cubul ABCDEFGH. Și așa mai departe pentru dimensiuni superioare.
Acestea sunt politopurile de măsură sau hipercuburile. Numele lor sunt, în ordinea dimensiunilor:
- 0. Punct
- 1. Segment
- 2. Pătrat (tetragon regulat)
- 3. Cub (hexaedru regulat)
- 4. Tesseract sau 4-cub
- 5. Penteract sau 5-cub
- ... Un n-cub are 2n vârfuri.
Ortoplecși[modificare | modificare sursă]

|

|

|
| Pătrat | Octaedru | 16-celule |

|

|

|
Se începe cu un punct O. Se extinde pe o dreaptă în direcții opuse până la punctele A și B la distanța r de la O și 2r între ele. Se trasează segmentul COD de lungime 2r, având mijlocul în O și fiind ortogonală pe AB. Se unesc capetele pentru a forma pătratul ACBD. Se trasează segmentul EOF de aceeași lungime și având mijlocul în O, ortogonal pe AB și CD (de exemplu „în sus” și „în jos”'). Se unesc aceste două capete cu vârfurile pătratului pentru a forma un octaedru regulat. Și așa mai departe pentru dimensiuni superioare.
Acestea sunt ortoplecși. Numele lor sunt, în ordinea dimensiunilor:
- 0. Punct
- 1. Segment
- 2. Pătrat (tetragon regulat)
- 3. Octaedru regulat
- 4. 4-ortoplex sau 16-celule
- 5. 5-ortoplex
- ... Un n-ortoplex are 2n vârfuri.
Istoria descoperirilor[modificare | modificare sursă]
Poligoane și poliedre convexe[modificare | modificare sursă]
Cea mai veche tratare matematică cunoscută a poligoanelor și poliedrelor este cea a matematicienilor din Grecia Antică. Aceștia cunoșteau cele cinci poliedre platonice. Pitagora știa despre cel puțin trei dintre ele, iar Theaetetus (c. 417 î.Hr. – 369 î.Hr.) le-a descris pe toate cinci. Mai târziu, Euclid a scris un studiu sistematic al matematicii, publicându-l sub titlul Elementele, care a construit o teorie logică a geometriei și a teoriei numerelor. Opera sa s-a încheiat cu descrieri matematice ale celor cinci poliedre platonice.
Poligoane și poliedre stelate[modificare | modificare sursă]
Multe secole după Euclid cunoștințele matematice nu au progresat. Istoria ulterioară a politopurilor regulate poate fi caracterizată printr-o lărgire treptată a conceptului de bază, permițând ca tot mai multe obiecte să fie luate în considerare. Thomas Bradwardine (Bradwardinus) a fost primul care a studiat serios poligoanele stelate. Diferite poliedre stelate apar în arta Renașterii, dar abia când Johannes Kepler a studiat în 1619 micul dodecaedru stelat și marele dodecaedru stelat a constatat că acestea erau regulate. Louis Poinsot a descoperit marele dodecaedru și marele icosaedru în 1809, iar Augustin Louis Cauchy a demonstrat în 1812 că lista este completă. Aceste poliedre sunt cunoscute drept poliedrele Kepler–Poinsot.
Poliedrele Kepler-Poinsot 



Micul
dodecaedru
stelatMarele
dodecaedru
stelatMarele
dodecaedruMarele
icosaedru
Politopuri din dimensiuni superioare[modificare | modificare sursă]

Abia în secolul al XIX-lea matematicianul elvețian, Ludwig Schläfli, a examinat și a descris politopurile regulate din dimensiunile superioare. Cercetările sale au fost publicate integral postum, în [1], la șase ani după decesul său, deși părți ale acestora au fost publicate în 1855[2] și 1958[3]. Între 1880 și 1900, rezultatele lui Schläfli au fost redescoperite independent de cel puțin alți nouă matematicieni — pentru detalii v. Coxeter.[4] Schläfli a numit o astfel de figură „polyschem” (română polischemă). Termenul „politop” a fost introdus în 1882 de Reinhold Hoppe, unul dintre cei care au redescoperit rezultatele lui Schläfli, și folosit pentru prima dată în limba engleză de Alicia Boole Stott, aproximativ douăzeci de ani mai târziu. Termenul „polyhedroid” (română poliedroid) a fost și el folosit în literatura anterioară (Hilbert, 1952).
Lucrarea lui Coxeter din 1948[5] este probabil cea mai cuprinzătoare lucrare care tratează rezultatele lui Schläfli și cele similare din domeniu până în prezent. Schläfli a arătat că există șase politopuri regulate convexe în 4 dimensiuni. Cinci dintre ele pot fi văzute ca fiind analogii poliedrelor platonice: 4-simplexul (sau 5-celule) cu tetraedrul, hipercubul (sau tesseractul) cu cubul, 4-ortoplexul (sau 16-celule) cu octaedrul, 120-celule cu dodecaedrul și 600-celule cu icosaedrul. Al șaselea, 24-celule, poate fi văzut ca o formă de tranziție între hipercub și 16-celule, similar cum cuboctaedrul și dodecaedrul rombic sunt forme de tranziție între cub și octaedru.
În cinci și mai multe dimensiuni, există exact trei politopuri regulate, care corespund tetraedrului, cubului și octaedrului: acestea sunt simplexurile regulate, hipercuburile și ortoplecșii. De asemenea, prezintă interes 4-politopurile regulate stelate, descoperite parțial de Schläfli.
La sfârșitul secolului al XIX-lea, matematicieni precum Arthur Cayley și Ludwig Schläfli au dezvoltat teoria politopurilor regulate în patru dimensiuni și mai mari, cum ar fi tesseractul și 24-celule. Acestea din urmă sunt dificil de vizualizat (deși nu imposibil), dar conservă totuși simetria plăcută din punct de vedere estetic a formelor asemănătoare din dimensiunile inferioare. Tesseractul conține 8 celule cubice. Se compune din două cuburi în hiperplane paralele cu vârfurile corespunzătoare conectate în așa fel încât cele 8 muchii transversale să fie egale în lungime și ortogonale cu cele 12 + 12 muchii situate pe fiecare cub. Fețele corespunzătoare ale celor două cuburi sunt conectate pentru a forma celelalte 6 fețe cubice ale tesseractului. 24-celule poate fi derivat din tesseract prin unirea celor 8 vârfuri ale fiecăreia dintre fețele sale cubice la un vârf suplimentar pentru a forma analogul în patru dimensiuni al unei piramide. Ambele figuri, precum și alte figuri în 4 dimensiuni pot fi vizualizate și descrise direct folosind stereografe în 4 dimensiuni.[6]
Mai greu de imaginat sunt politopurile abstracte moderne, cum ar fi 57-celule sau 11-celule. Din punct de vedere matematic aceste obiecte au aceleași calități estetice ca și rudele lor mai familiare din două și trei dimensiuni.
La începutul secolului al XX-lea, definițiile politopurilor regulate erau:
- Un poligon regulat este un poligon ale cărui laturi sunt toate egale și ale căror unghiuri sunt toate egale.
- Un poliedru regulat este un poliedru ale cărui fețe sunt toate poligoane regulate congruente și ale căror figuri ale vârfului sunt toate congruente și regulate.
- Și așa mai departe, un n-politop regulat este un politop n-dimensional ale cărui fețe (n−1)-dimensionale sunt toate regulate și congruente și ale căror figuri ale vârfului sunt toate regulate și congruente.
Aceasta este o definiție „recursivă”. Ea definește regularitatea formelor din dimensiuni superioare în termenii formelor regulate din dimensiuni inferioare. Există o definiție echivalentă (nerecursivă), care afirmă că un politop este regulat dacă are un grad de simetrie suficient.
- Un n-politop este regulat dacă orice mulțime formată dintr-un vârf, o latură incidentă, o față bidimensională care conține latura respectivă, și tot așa până la dimensiunea n − 1 poate fi aplicată pe orice asemenea mulțime prin simetrii ale politopului.
De exemplu, cubul este regulat deoarece dacă alegem un vârf al cubului și una dintre cele trei laturi incidente la el, și una dintre cele două fețe care conțin latura, atunci acest triplet sau steag, (vârf, latură, față) poate fi suprapus la orice alt astfel de steag printr-o simetrie adecvată a cubului. Astfel se poate defini succint un politop regulat drept:
- Un politop regulat este unul al cărui grup de simetrie este tranzitiv pe steagurile sale.
În secolul al XX-lea au fost câteva evoluții importante. Grupurile de simetrie ale politopurilor clasice regulate au fost generalizate în ceea ce se numesc acum grupuri Coxeter. Grupurile Coxeter includ, de asemenea, grupurile de simetrie ale teselărilor regulate ale spațiului sau planului. De exemplu, grupul de simetrie al unei table de șah infinite ar fi grupul Coxeter [4,4].
Apeirotopuri — politopuri infinite[modificare | modificare sursă]
În prima parte a secolului al XX-lea, Coxeter și Petrie au descoperit trei structuri infinite {4, 6}, {6, 4} și {6, 6}. Le-au numit poliedre regulate strâmbe, deoarece păreau să satisfacă definiția unui poliedru regulat — toate vârfurile, laturile, fețele și unghiurile sunt congruente, iar figura nu are fețe libere. În zilele noastre, ele sunt numite apeiroedre sau poliedre infinite. Pavările regulate ale planului {4, 4}, {3, 6} și {6, 3} pot fi, de asemenea, considerate ca poliedre infinite.
În anii 1960 Branko Grünbaum a lansat un apel către comunitatea geometrilor de a lua în considerare tipuri mai abstracte de politopuri regulate polystromata (română polistromate). El a dezvoltat teoria polistromatelor, prezentând exemple de obiecte noi pe care le-a numit apeirotopuri regulate, adică politopuri regulate cu un număr infinit de fețe. Un exemplu simplu de apeirogon necoliniar ar fi un zigzag. Se pare că acesta satisface definiția unui poligon regulat — toate laturile au aceeași lungime, toate unghiurile sunt congruente, iar figura nu are capete libere (deoarece nu pot fi atinse niciodată). Mai important, poate, există simetrii ale zigzagului care pot suprapune orice pereche de vârf plus latură incidentă pe oricare alta. De atunci au continuat să fie descoperite și alte apeirogoane regulate și apeirotopuri în dimensiuni superioare.
Politopuri complexe regulate[modificare | modificare sursă]
Un număr complex are o parte reală, care este partea familiară tuturor și o parte imaginară, care este un multiplu al rădăcinii pătrate a lui –1. Un spațiu Hilbert complex are coordonatele x, y, z… numere complexe. Acest lucru practic dublează numărul de dimensiuni. Un politop construit într-un astfel de spațiu unitar se numește politop complex(d).[7]
Politopuri abstracte[modificare | modificare sursă]

Grünbaum a descoperit și 11-celule, un obiect autodual 4-dimensional ale cărui fațete nu sunt icosaedre, ci sunt „hemiicosaedre” — adică sunt forma care se obține dacă se consideră că fețele opuse ale icosaedrelor sunt de fapt „aceeași” față [8]. Hemiicosaedrul are doar 10 fețe triunghiulare și 6 vârfuri, spre deosebire de icosaedru, care are 20, respectiv 12.
Acest concept poate fi mai ușor de înțeles pentru cititor dacă se ia în considerare analogia dintre cub și hemicub. Un cub obișnuit are 8 vârfuri, care ar putea fi etichetate de la A la H, cu A opus lui H, B opus lui G etc. Într-un hemicub, A și H ar fi considerate același vârf. La fel ar fi B și G etc. Latura AB ar deveni aceeași latură cu GH, iar fața ABEF ar deveni aceeași față cu CDGH. Noua formă are doar trei fețe, 6 laturi și 4 vârfuri.
11-celule nu poate fi materializat în geometria din spațiul euclidian, ci numai în hiperspațiul curbat pozitiv (eliptic).
La câțiva ani după descoperirea lui 11-celule de Grünbaum, Coxeter a descoperit independent aceeași formă. El descoperise mai devreme un politop similar, 57-celule.[9]
Până în 1994 Grünbaum considera politopurile abstracte drept mulțimi combinatorice de puncte sau vârfuri, și nu se preocupa dacă fețele erau plane. Pe măsură ce el și alții au dezvoltat aceste idei, astfel de mulțimi au ajuns să fie numite politopuri abstracte. Un politop abstract este definit drept o mulțime parțial ordonată, ale cărui elemente sunt fețele politopului (vârfuri, laturi, fețe etc.) ordonate de conținut. Mulțimii îi sunt impuse anumite restricții, similare cu proprietățile satisfăcute de politopurile regulate clasice (inclusiv corpurile lui Platon). Totuși, restricțiile sunt suficient de laxe încât teselările regulate, hemicuburile și chiar obiecte ca 11-celule sau chiar mai ciudate să fie exemple de politopuri regulate.
Un politop geometric este privit ca o materializare a unui politop abstract, astfel încât există o corespondență biunivocă între elementele abstracte și cele geometrice. Astfel orice politop geometric poate fi descris de mulțimea abstractă adecvată, deși nu toate politopurile abstracte au materializările geometrice corespunzătoare.
Ulterior teoria a fost dezvoltată în special de McMullen și Schulte,[10] dar și alți cercetători au avut contribuții.
Regularitatea politopurilor abstracte[modificare | modificare sursă]
Regularitatea are o anumită semnificație, deși pentru politopurile abstracte ea este diferită deoarece unghiurile și lungimile laturilor nu au sens. Definiția regularității, așa cum este prezentată în introducere, se aplică politopurilor abstracte în termeni de tranzitivitate a steagurilor.
Orice politop regulat clasic are un echivalent abstract care este regulat, obținut din mulțimea de fețe. Dar politopurile neregulate clasice pot avea echivalente regulate abstracte, deoarece politopurile abstracte nu țin cont, de exemplu, de mărimile unghiurilor și de lungimile laturilor. Iar un politop regulat abstract se poate să nu poată fi materializat ca politop clasic. De exemplu, în domeniul abstract toate poligoanele sunt regulate, în timp ce în geometria clasică sunt regulate doar cele care au laturile și unghiurile egale.
Figura vârfului politopurilor abstracte[modificare | modificare sursă]
La politopurile abstracte noțiunea de figura vârfului este și ea definită în mod diferit. Figura vârfului V a unui n-politop abstract este mulțimea tuturor fețelor abstracte care conțin pe V, inclusiv pe V în sine. Formal, este secțiunea abstractă
- Fn / V = {F | V ≤ F ≤ Fn}
unde Fn este cel mai înalt tip de față, adică n-fața care conține toate celelalte tipuri de fețe. De notat că fiecare i-față, i ≥ 0 a politopului original devine o (i – 1)-față a figurii vărfului.
Spre deosebire de politopurile euclidiene, un politop abstract cu fațete și figuri de vârf regulate poate fi sau nu el însuși unul regulat — de exemplu piramida pătrată, ale cărei fațete și figuri de vârf sunt poligoane abstracte regulate. Totuși, în cazul politopurilor clasice figura vârfului va fi o materializare a celei abstracte.
Construcții[modificare | modificare sursă]
Poligoane[modificare | modificare sursă]
Modul tradițional de a construi un poligon regulat, sau orice altă figură în plan, este cu rigla (negradată) și compasul. Construirea unor poligoane regulate în acest mod este foarte simplă (cel mai ușor este, probabil, triunghiul echilateral), unele sunt mai complexe, iar altele sunt imposibile („nu pot fi construite”). Cele mai simple câteva poligoane regulate care nu pot fi construite sunt poligoanele cu „n” laturi, unde „n” este egal cu 7, 9, 11, 13, 14, 18, 19, 21, ...
Ideal, aceste construcții se referă la cele executate cu instrumente ideale. Bineînțeles, prin diferite metode se pot face construcții aproximative rezonabil de precise; în timp ce unele construcții, posibile teoretic, sunt nepractice.
Poliedre[modificare | modificare sursă]
Elementele lui Euclid au prezentat construcțiile cu rigla și compasul ale celor cinci poliedre platonice.[11] Totuși, simpla întrebare practică a modului în care s-ar putea trasa o linie dreaptă în spațiu, chiar și cu o riglă, ar putea conduce la întrebarea ce înseamnă exact să fie „construit” un poliedru regulat. (Desigur, s-ar putea pune aceeași întrebare pentru poligoane.)

Termenul „construcție” are conotația realizării practice a obiectului construit. Modul obișnuit de a construi un poliedru regulat este prin intermediul desfășuratei lui. Pentru a obține o figură pliabilă a unui poliedru, se ia suprafața poliedrului și se taie suficient de-a lungul unor margini astfel încât suprafața să poată fi desfășurată. Poliedrele platonice au fețele formate doar din triunghiuri, pătrate și pentagoane, care pot fi construite cu rigla și compasul, deci și desfășuratele lor. Același lucru este valabil și pentru poliedrele stelate, deși aici trebuie atenție pentru a trasa doar fețele exterioare vizibile.
Dacă desfășurata este trasată pe carton sau pe un material pliabil similar (de exemplu, tablă), desfășurata poate fi decupată, îndoită de-a lungul laturilor netăiate, iar restul laturilor unite corespunzător pentru a forma poliedrul pentru care a fost trasată desfășurata. Pentru un poliedru dat pot exista multe desfășurate. De exemplu, pentru cub există 11, iar pentru dodecaedru peste 900000.[12]
Numeroase jucării pentru copii sau adolescenți oferă experiențe cu poligoane și poliedre regulate. De exemplu, klikko oferă seturi de plastic cu triunghiuri, pătrate, pentagoane și hexagoane care pot fi unite de la margine la margine într-un număr mare de moduri diferite. Un copil care se joacă cu o astfel de jucărie ar putea descoperi din nou poliedrele platonice (sau chiar cele ale lui Arhimede), mai ales dacă ar fi puțin îndrumat de la un adult cu cunoștințe.
Teoretic, aproape orice material poate fi folosit pentru a construi poliedre regulate, de exemplu din hârtie.[13] Ele pot fi sculptate din lemn, modelate din sârmă, formate din vitralii. Limita depinde de imaginație.
Dimensiuni superioare[modificare | modificare sursă]



În dimensiuni superioare este mai greu de descris „construirea” obiectelor. Desigur, într-un univers tridimensional este imposibil de construit un model fizic al unui obiect având 4 sau mai multe dimensiuni. Această chestiune poate fi abordată în mai multe feluri.
Prima abordare, potrivită pentru patru dimensiuni, utilizează stereografia în patru dimensiuni.[6] Adâncimea într-a treia dimensiune este reprezentată ca deplasare relativă orizontală, iar adâncimea într-a patra dimensiune ca deplasare relativă verticală între imaginile din stânga și dreapta privite prin stereograf.
A doua abordare este de a reprezenta obiectele din dimensiuni superioare în spațiul tridimensional utilizând metode analoage modurilor în care obiecte tridimensionale sunt desenate în plan. De exemplu, desfășuratele pliate menționate în secțiunea anterioară au echivalente în dimensiuni superioare. S-ar putea chiar imagina construirea unui model al acestei desfășurate așa cum se desenează o desfășurată a unui poliedru pe o bucată de hârtie. Din păcate, din cauza constrângerilor universului fizic nu este posibilă plierea necesară a unei structuri tridimensionale pentru a obține un politop 4-dimensional. O altă modalitate de a „trasa” în 3 dimensiuni formele cu dimensiuni superioare este prin intermediul unui procedeu de proiecție, de exemplu prin proiecția ortogonală sau în perspectivă. Faimoasa lucrare a lui Coxeter despre politopuri[5] prezintă câteva exemple de astfel de proiecții ortogonale. Alte exemple se pot vedea la MathWorld, de exemplu pentru un 600-celule.[14] De notat că proiectarea directă a unui 4-politop în două dimensiuni poate produce confuzie. Mai ușor de înțeles sunt modelele 3D ale proiecțiilor. Astfel de modele se găsesc ocazional în muzeele științifice sau în departamentele de matematică ale universităților (cum ar fi Université Libre de Bruxelles).
Intersecția unui politop regulat 4-dimensional (sau mai mare) cu un hiperplan tridimensional va fi un politop (nu neapărat regulat). Dacă hiperplanul este deplasat prin formă, feliile tridimensionale pot fi combinate și animate într-un fel de obiect 4-dimensional, unde a patra dimensiune este considerată a fi timpul. Prin intermediul unor astfel de secțiuni transversale se poate vizualiza întreaga structură a politopurilor regulate 4-dimensionale.
Procedeul este analog celui prin care tomografia computerizată(d) asamblează imaginile bidimensionale pentru a realiza reprezentări tridimensionale ale organelor scanate. Idealul ar fi o hologramă animată. Totuși, chiar și o animație simplă, cum este cea prezentată alături, poate oferi deja o perspectivă — cei drept, limitată — asupra structurii politopului.
Altă cale în care o persoană care vizualizează tridimensional poate înțelege structura unui politop 4-dimensional este prin „a fi cufundat” în obiect, poate printr-o formă de realitate virtuală. Pentru a înțelege cum ar putea funcționa acest lucru, se poate imagina ce s-ar vedea dacă spațiul ar fi umplut cu cuburi. Privitorul ar fi în interiorul unuia dintre cuburi și ar putea vedea cuburi în fața, în spate, deasupra, dedesubt, la stânga și la dreapta lui. Dacă s-ar putea călători în aceste direcții, s-ar putea explora matricea de cuburi și ar putea înțelege structura sa geometrică. O matrice infinită de cuburi nu este un politop în sens tradițional. De fapt, este o teselare a spațiului tridimensional (euclidian). Cu toate acestea, un 4-politop poate fi considerat o teselare a unui spațiu tridimensional neeuclidian, și anume, o teselare a suprafeței unei sfere 4-dimensionale (o pavare sferică 4-dimensională).

La nivel local, acest spațiu pare a fi cel familiar și, prin urmare, un sistem de realitate virtuală ar putea, în principiu, să fie programat pentru a permite explorarea acestor „teselări”, adică a politopurilor regulate 4-dimensionale. Departamentul de matematică de la UIUC are o serie de imagini cu ceea ce s-ar vedea într-o teselare cu dodecaedre dintr-un spațiu hiperbolic. O astfel de teselare este un exemplu de politop regulat abstract infinit.
În mod normal, pentru politopurile abstracte regulate, un matematician consideră că obiectul este „construit” dacă se cunoaște structura grupului său de simetrie. Acest lucru se datorează unei teoreme importante în studiul politopurilor regulate abstracte, oferind o tehnică care permite ca politopul regulat abstract să fie construit direct din grupul său de simetrie într-un mod simplu.
Note[modificare | modificare sursă]
- ^ Schläfli, Theorie…, 1901
- ^ Schläfli, Réduction…, 1855
- ^ Schläfli, On the multiple…, 1858
- ^ Coxeter Regular…, 1948, pp. 143–144
- ^ a b Coxeter Regular…, 1948
- ^ a b en Brisson, David W. () [1978]. „Visual Comprehension in n-Dimensions”. În Brisson, David W. Hypergraphics: Visualizing Complex Relationships In Arts, Science, And Technololgy. AAAS Selected Symposium. 24. Taylor & Francis. pp. 109–145. ISBN 978-0-429-70681-3.
- ^ Coxeter, Regular…, 1974
- ^ Grünbaum, Regularity of…
- ^ Coxeter, 1982, 1984
- ^ McMullen, Schulte Abstract…, 2002
- ^ en Euclid, Elements, accesat 2007-10-28 (arhivă)
- ^ en Polyhedral Maps, accesat 2008-08-15 (arhivă)
- ^ en Polyedra classification, accesat 2004-10-11 (arhivă)
- ^ en 600-Cell, MathWorld, accesat 2021-01-19
Bibliografie[modificare | modificare sursă]
- en Coxeter, H. S. M., Regular Polytopes, Methuen and Co., 1948
- en Coxeter, H.S.M. (). Regular Polytopes (ed. 3rd). Dover. ISBN 0-486-61480-8.
- en — (). Regular Complex Polytopes
 . Cambridge University Press. ISBN 052120125X.
. Cambridge University Press. ISBN 052120125X. - en — (). Regular Complex Polytopes (ed. 2nd). Cambridge University Press. ISBN 978-0-521-39490-1.
- en Cromwell, Peter R. (). Polyhedra. Cambridge University Press. ISBN 978-0-521-66405-9.
- en Euclid (). Elements. Cambridge University Press.
- en Grünbaum, B. (). Regularity of Graphs, Complexes and Designs. Problèmes Combinatoires et Théorie des Graphes, Colloquium Internationale CNRS, Orsay. 260. pp. 191–197.
- en Grünbaum, B. (). „Polyhedra with hollow faces”. În Bisztriczky, T.; et al. POLYTOPES: abstract, convex, and computational. Mathematical and physical sciences, NATO Advanced Study Institute. 440. Kluwer Academic. pp. 43–70. ISBN 0792330161.
- en McMullen, P.; Schulte, S. (). Abstract Regular Polytopes
 . Cambridge University Press.
. Cambridge University Press. - en Sanford, V. (). A Short History Of Mathematics. The Riverside Press.
- fr Schläfli, L. (). „Réduction d'une intégrale multiple, qui comprend l'arc de cercle et l'aire du triangle sphérique comme cas particuliers”. Journal de Mathématiques. 20: 359–394.
- en Schläfli, L. (). „On the multiple integral ∫^ n dxdy... dz, whose limits are p_1= a_1x+ b_1y+…+ h_1z> 0, p_2> 0,..., p_n> 0, and x^ 2+ y^ 2+…+ z^ 2< 1”. Quarterly Journal of Pure and Applied Mathematics. 2: 269–301. 3 (1860) pp54–68, 97–108.
- de Schläfli, L. (). „Theorie der vielfachen Kontinuität”. Denkschriften der Schweizerischen Naturforschenden Gesellschaft. 38: 1–237.
- en Smith, J. V. (). Geometrical and Structural Crystallography (ed. 2nd). Wiley. ISBN 0471861685.
- en Van der Waerden, B. L. (). Science Awakening
 . P Noordhoff.
. P Noordhoff. - en D.M.Y. Sommerville () [1930]. „X. The Regular Polytopes”. Introduction to the Geometry of n Dimensions. Courier Dover. pp. 159–192. ISBN 978-0-486-84248-6.
Legături externe[modificare | modificare sursă]
 Materiale media legate de politop regulat la Wikimedia Commons
Materiale media legate de politop regulat la Wikimedia Commons- en The Atlas of Small Regular Polytopes, Lista politopurilor regulate.
| Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familie | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Poligoane regulate | Triunghi | Pătrat | p-gon | Hexagon | Pentagon | |||||||
| Poliedre uniforme | Tetraedru | Octaedru • Cub | Semicub | Dodecaedru • Icosaedru | ||||||||
| 4-politopuri uniforme | 5-celule | 16-celule • Tesseract | Semitesseract | 24-celule | 120-celule • 600-celule | |||||||
| 5-politopuri uniforme | 5-simplex | 5-ortoplex • 5-cub | 5-semicub | |||||||||
| 6-politopuri uniforme | 6-simplex | 6-ortoplex • 6-cub | 6-semicub | 122 • 221 | ||||||||
| 7-politopuri uniforme | 7-simplex | 7-ortoplex • 7-cub | 7-semicub | 132 • 231 • 321 | ||||||||
| 8-politopuri uniforme | 8-simplex | 8-ortoplex • 8-cub | 8-semicub | 142 • 241 • 421 | ||||||||
| 9-politopuri uniforme | 9-simplex | 9-ortoplex • 9-cub | 9-semicub | |||||||||
| 10-politopuri uniforme | 10-simplex | 10-ortoplex • 10-cub | 10-semicub | |||||||||
| n-politopuri uniforme | n-simplex | n-ortoplex • n-cub | n-semicub | 1k2 • 2k1 • k21 | n-politop pentagonal | |||||||
| Topicuri: Familii de politopuri • Politop regulat | ||||||||||||