Mulțime
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. |
Mulțimea este unul dintre cele mai importante concepte ale matematicii moderne. Deși teoria mulțimilor a apărut abia la sfârșitul secolului XIX, aceasta este acum omniprezentă în educația matematică, încă din școala elementară. Acest articol este o scurtă introducere în ceea ce matematicienii numesc „teoria naivă a mulțimilor”. Pentru considerații istorice și o introducere la teorii axiomatice ale mulțimilor, vezi teoria mulțimilor.
Mulțimea este o noțiune primară care nu se definește prin raportare la alte noțiuni mai generale, ci se descrie / se definește ostensiv. O descriere intuitivă a conceptului este dată de considerarea mulțimii drept un număr de elemente oarecare puse laolaltă, adică o reuniune de singletoni. Numărul de elemente al unei mulțimi e denumit și cardinalitate sau număr cardinal. Pentru mulțimile infinite și mai ales infinite nenumărabile se folosește termenul cardinalitate, și nu numărul de elemente, care ar fi neclar. În cazul mulțimilor infinite pot apărea paradoxuri, pentru a căror evitare au fost construite teorii axiomatice ale mulțimilor.
Introducere[modificare | modificare sursă]
În mod neriguros o mulțime este un ansamblu bine definit de obiecte, considerată ca un întreg. Obiectele individuale dintr-o mulțime sunt numite elemente. Elementele unei mulțimi pot fi de orice natură: numere, litere ale alfabetului, simboluri grafice, persoane, alte mulțimi etc.
Prin convenție, mulțimile sunt notate cu majuscule cursive: A, B, C etc.
Două mulțimi A și B se numesc egale sau identice, și aceasta se notează A = B, dacă dețin (sunt formate din) aceleași elemente.
Descrierea mulțimilor[modificare | modificare sursă]
Descrierea folosind cuvinte sau liste[modificare | modificare sursă]
Nu toate mulțimile au descrieri precise; ele pot fi doar colecții arbitrare, fără vreo regulă exprimabilă, care să specifice care anume elemente fac parte dintr-o mulțime.
Unele mulțimi pot fi descrise în cuvinte, cum ar fi:
- A este mulțimea primelor patru numere naturale.
- B este mulțimea culorilor de pe steagul Franței.
Prin convenție, o mulțime poate fi definită listând explicit elementele sale între acolade, de exemplu:
- C = {0, 1, 2, 3}
- D = {roșu, alb, albastru}
De notat că cele două descrieri diferite definesc aceeași mulțime. De exemplu, pentru mulțimile definite mai sus, A și C sunt identice, deoarece ele au exact aceiași membri. Notația A = C este folosită pentru a exprima această egalitate. Analog, pentru mulțimile definite mai sus, B = D.
Identitatea mulțimilor nu depinde de ordinea în care elementele sunt listate, nici de prezența repetițiilor în listă. De exemplu, {6, 11} = {11, 6} = {11, 11, 6, 6}.
Descrierea folosind notații matematice[modificare | modificare sursă]
Pentru mulțimi mari (cu multe elemente) scrierea întregii liste de elemente conținute poate deveni nepracticabilă. De exemplu, E = {primele o mie de numere pozitive} ar fi, ca listă, foarte greoaie - atât la scris cât și la citit. Totuși matematicienii rareori descriu o mulțime de genul E în cuvinte, ca mai sus, preferând să folosească formulări simbolice:
Pentru a descrie o mulțime de genul mulțimii E se poate folosi uneori și o listă abreviată, unde elementele specificate urmează un șablon (un model, o schemă) evident cititorului. Faptul că se folosește o abreviere este atunci indicat explicit prin simbolul „...” (trei puncte).
Când se folosește această notație, trebuie avut grijă să se indice suficiente elemente pentru a face clar șablonul. De exemplu, următoarea mulțime ar putea să reprezinte, în funcție de context, atât primele șaisprezece numere întregi, cât și primele cinci puteri ale lui doi (cât și alte mulțimi), fiind deci neclară (neunivocă):
Un alt pericol apare dacă proprietatea definitorie implică un șablon mai puțin evident, în care cazuri listele abreviate chiar trebuie evitate. De exemplu, definiția (derutantă)
ar putea fi doar cu greu interpretată drept identică cu definiția (clară)
- F = {primele douăzeci de numere mai mici cu patru decât un pătrat perfect},
și în plus chiar și această ultimă definiție ar putea fi falsă, deoarece numărul de reguli care să producă mulțimea F de mai sus este nesfârșit (infinit).
În asemenea condiții, matematicienii descriu proprietatea caracteristică a membrilor mulțimii folosind o notație matematică. De exemplu:
În această descriere, bara verticală („|”) se citește cu proprietatea că (sau astfel încât). În loc de bara verticală se mai poate folosi și simbolul două puncte („:”). Formula de mai sus se citește:
- F este mulțimea numerelor de forma , unde n este un număr întreg cuprins între 0 și 19 inclusiv.
Evident că se poate forma și o listă explicită, completă, a conținutului (a membrilor) lui F, prin evaluarea expresiei pentru fiecare valoare a lui n de la 0 la 19.
Apartenența la mulțime[modificare | modificare sursă]
Conceptul care descrie dacă un obiect este sau nu element al unei anumite mulțimi (altfel spus, dacă îi aparține sau nu) este notat cu simbolurile și respectiv . Astfel, considerând mulțimile definite mai sus:
- 3 și 285 (deoarece 285 = 17² − 4); dar
- 9 și "verde" .
Simbolul al apartenenței a fost introdus de către matematicianul italian Giuseppe Peano în anul 1889, iar apoi adus la forma actuală de către matematicianul englez Bertrand Russel, în 1903. Această metodă de notație permite transcrierea unei propoziții cum ar fi „Socrate este muritor” în forma matematizată :
- (elementul Socrate aparține mulțimii muritorilor).
Cardinalitatea unei mulțimi[modificare | modificare sursă]
- Articol principal: Cardinal (matematică)
Cardinalitatea, numită și "puterea" unei mulțimi, desemnează bogăția ei de membri. Fiecare mulțime descrisă mai sus are un număr bine definit și finit de membri; de exemplu mulțimea de mai sus are patru membri, pe când mulțimea are trei membri. La mulțimile finite, cardinalitatea este chiar numărul respectiv de membri. Cardinalitatea mulțimilor se notează punând mulțimea între bare verticale, de exemplu B.
O mulțime poate avea și zero membri (niciun membru). O astfel de mulțime este denumită mulțimea vidă (sau mulțimea nulă) și este reprezentată prin simbolul . Există o singură mulțime nulă.
O mulțime poate avea însă și un număr infinit (nesfârșit) de mare de membri; de exemplu, mulțimea tuturor punctelor (idealizate) de pe o linie (idealizată și ea); mulțimea tuturor numerelor iraționale. În ceea ce privește bogăția lor în membri, există mai multe soiuri de mulțimi infinite (de infinituri), și anume unele mai bogate, iar altele mai puțin bogate în membri.
Pentru compararea cardinalităților a 2 mulțimi infinite, în loc de a încerca să se numere întâi separat membrii lor și apoi să se compare cele 2 rezultate, se folosește metoda "împerecherii" membrilor lor: se cercetează dacă poate fi găsită măcar o singură corespondență biunivocă (1 la 1) între cele 2 mulțimi atunci când ele se iau membru cu membru (altfel spus, dacă există o "funcție bijectivă" sau o bijecție între cele 2 mulțimi), sau dacă nu cumva în una din cele 2 mulțimi de comparat, după orice încercare de "împerechere" pe baza unei reguli, rămâne totuși întotdeauna un surplus de membri ne-împerecheați. În acest caz mulțimea cu surplusul are o cardinalitate (putere) mai mare decât cealaltă.
Au fost dovedite următoarele proprietăți neașteptate ale mulțimilor infinite:
- Există o cea mai "mică" mulțime infinită. Este vorba de orice parte infinită din mulțimea numerelor naturale. Cardinalitatea ei se notează cu , care se citește "alef zero", (alef) fiind prima literă din alfabetul ebraic. Astfel de mulțimi se numesc "numărabile", deoarece sunt echipotente cu mulțimea numerelor naturale 1, 2, 3,... . Reunind 2 mulțimi infinite de putere , rezultă o mulțime infinită tot de putere . Exemple concrete de mulțimi infinite cu cardinalitatea : toate numerele prime; toate numerele impare; toate numerele raționale.
- O mulțime infinită cu puterea mai mare decât este de exemplu mulțimea punctelor de pe o dreaptă, sau și mulțimea punctelor dintr-un pătrat, aceste două mulțimi fiind echipotente. Puterea lor se notează cu litera (alef) sau și cu un (c gotic). Această notație provine de la cuvântul latin „continuum”. Astfel de mulțimi se mai numesc și „de puterea continuului”.
- S-a dovedit că nu se poate deduce dacă există sau nu mulțimi cu puterea situată între și . Altfel spus, sunt permise ambele ipoteze: atât ipoteza continuului, cât și contrara acesteia.
- Puterea care urmează după o are de exemplu mulțimea tuturor funcțiilor care se pot defini pe o mulțime de putere . Această putere se notează cu (f gotic).
- O putere și mai mare o are mulțimea tuturor funcțiilor care se pot defini pe o mulțime de putere .
- În felul acesta se pot construi (mental) mulțimi infinite cu puteri din ce în ce mai mari, fără o limită superioară.
Cercetările cele mai recente încearcă să găsească o nouă axiomă independentă de sistemul de axiome ZFC care, adăugată la sistemul ZFC, rezolvă problemele actuale legate de ipoteza continuului. Există deja 2 candidați pentru o astfel de axiomă nouă, numiți unul Projective Determinacy (PD) și celălalt Woodin's Martin's Maximum (WMM). Conform acestora se pare că ipoteza continuului este falsă, deci ar exista o cardinalitate, probabil chiar una singură, situată între și
Submulțimi[modificare | modificare sursă]

Dacă fiecare membru al mulțimii A este și membru al mulțimii B, atunci A se spune că este submulțime a lui B, și se scrie că , citit și A este inclus în B. Echivalent, putem scrie , citit B include A, sau B conține A. Relația dintre mulțimi stabilită de se numește incluziune sau conținere.
Dacă A este o submulțime a lui B, dar nu este egală cu B, atunci A se numește submulțime proprie a lui B, ceea ce se scrie sau . Totuși, în literatură aceste simboluri se citesc la fel ca și , deci se preferă adesea să se folosească simbolurile mai explicite și și pentru incluziunea strictă.
Exemple:
- Mulțimea tuturor femeilor este o submulțime a mulțimii tuturor oamenilor.
- {1,3} {1,2,3,4}
- {1,2,3,4} {1,2,3,4}
Mulțimea vidă este o submulțime a tuturor mulțimilor și orice mulțime este o submulțime a ei însăși:
Mulțimea părților[modificare | modificare sursă]
o mulțime numită mulțimea părților lui , astfel încât
Altfel spus, fiind dată o mulțime , există o mulțime astfel încât elementele lui sunt submulțimile lui . Mulțimea este unic determinată de mulțimea deoarece presupunând prin reducere la absurd că o altă mulțime care satisface condiția , atunci pentru orice mulțime rezultă: Din axioma extensionalității obținem că , ca atare este unic determinată de mulțimea .
Notația tradițională pentru mulțimea părților lui este
Pentru o mulțime finită cu elemente, cardinalul mulțimii părților se calculează ca o sumă a numerelor de mulțimi cu elemente. Pentru avem un singur element, mulțimea vidă . Pentru mulțimea părților are exact submulțimi de un singur element ale lui . În general, pentru orice va conține exact combinări de n luate câte k submulțimi cu elemente
Mulțimi speciale[modificare | modificare sursă]
Există unele mulțimi care au atât de mare importanță matematică și sunt referite atât de des încât ele au obținut nume și notații simbolice speciale, pentru a se opera mai ușor cu ele. Una din acestea este mulțimea vidă . Alte mulțimi speciale de numere sunt:
- reprezintă mulțimea tuturor numerelor naturale. Adică = {0, 1, 2, 3, ...}, sau uneori * = {1, 2, 3, ...}.
- reprezintă mulțimea tuturor numerelor întregi (pozitive, negative sau zero). Deci = {..., -2, -1, 0, 1, 2, ...}.
- reprezintă mulțimea tuturor numerelor raționale (adică mulțimea tuturor fracțiilor proprii și improprii). Astfel, . De exemplu, și . Toți întregii sunt în această mulțime deoarece fiecare întreg a poate fi exprimat ca fracția .
- reprezintă mulțimea tuturor numerelor reale. Aceasta include toate numerele raționale, împreună cu toate numerele iraționale (adică numere care nu pot fi scrise ca fracții, cum ar fi , și ).
- Vezi și articolul Număr hiperreal.
- este mulțimea tuturor numerelor complexe.
Se observă că ; toate aceste mulțimi au un număr infinit de membri, dar cardinalitățile lor sunt diferite:
, care este mai mic decât .
Operații cu mulțimi[modificare | modificare sursă]
Reuniunea[modificare | modificare sursă]

Există mai multe moduri de a construi o mulțime nouă din alta sau altele deja existente. Două mulțimi pot fi "adunate". Operația, numită "reuniunea" lui A cu B și notată A U B, este mulțimea tuturor entităților care sunt membri fie ai lui A, fie ai lui B.
Exemple:
Unele proprietăți de bază ale reuniunii:
În cazul a n mulțimi, reuniunea acestora mai poate fi notată:
În cazul general, când indicii mulțimilor aparțin unei mulțimi reuniunea poate fi notată:
Intersecția[modificare | modificare sursă]

O nouă mulțime poate fi construită și prin determinarea membrilor pe care două mulțimi date îi au în comun. Intersecția dintre A și B, notată A ∩ B, este mulțimea tuturor entităților (membrilor) care aparțin atât mulțimii A cât și mulțimii B. Dacă A ∩ B = ø, atunci A și B se numesc mulțimi disjuncte (fără membri comuni).
Exemple:
Proprietăți de bază ale intersecțiilor:
În cazul a n mulțimi, intersecția acestora mai poate fi notată:
În cazul general, când indicii mulțimilor aparțin unei mulțimi intersecția poate fi notată:
Diferența, complementarea[modificare | modificare sursă]
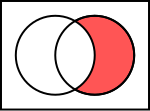
Două mulțimi pot fi "scăzute". Complementul relativ al lui A în B (numit și diferența dintre mulțimile B și A), notat B − A (sau și B \ A), este mulțimea tuturor elementelor care fac parte din B, dar nu și din A. De notat că nu este greșit să se "scoată" dintr-o mulțime elemente care nu îi aparțin, cum ar fi eliminarea elementului verde din mulțimea {1,2,3}; doar că această operație nu are nici un efect.
În anumite cazuri, toate mulțimile despre care se discută sunt considerate submulțimi ale unei mulțimi universale U. În astfel de cazuri U − A se numește complementul absolut (față de U), sau pur și simplu complementul lui A, și este notat cu A′.
Exemple:
- Dacă U este mulțimea numerelor întregi, E este mulțimea întregilor pari, și O este mulțimea întregilor impari, atunci complementul lui E față de U este O: .
Proprietăți de bază ale complementelor:
Diferența simetrică[modificare | modificare sursă]
Diferența simetrică a mulțimilor A și B este mulțimea:
Proprietăți de bază ale diferenței simetrice:
Produsul cartezian[modificare | modificare sursă]
Bibliografie[modificare | modificare sursă]
- en Halmos, Paul R., Naive Set Theory, Princeton, N.J.: Van Nostrand (1960) ISBN 0-387-90092-6
- en Stoll, Robert R., Set Theory and Logic, Mineola, N.Y.: Dover Publications (1979) ISBN 0-486-63829-4
- N. I. Vilenkin, excursie în teoria mulțimilor, editura enciclopedică română, București, 1972
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
| |||||||||||||||||||||||||||||||||||







































































































