Matematică recreativă

Matematica recreativă include o multitudine de jocuri matematice și poate fi extinsă ca noțiune și pentru puzzle-urile și problemele de logică sau deducție. Nici chiar unele dintre cele mai interesante probleme din această arie nu necesită cunoștințe de matematică avansată.
Tot în această categorie sunt incluse și subiecte precum estetica matematicii dar și povestioare amuzante sau coincidențe despre matematică în general sau despre matematicieni. Cea mai importantă contribuție pe care o aduce acest domeniu este faptul că stimulează curiozitatea și inspiră dorința de aprofundare în studii ulterioare.
Cele mai cunoscute exemple din matematica recreativă sunt careurile magice sau pătratele magice. În general, matematica recreativă poate fi împărțită în două mari categorii: jocuri și puzzle-uri. Pe scurt, puzzle-urile nu au decât un jucător pe când jocurile au doi sau mai mulți jucători.
Pătratele magice[modificare | modificare sursă]
Un pătrat magic de ordinul n este un aranjament de n2 numere, de obicei numere naturale sau întregi, distincte, astfel încât numerele de pe linie, de pe coloană și pe diagonală, însumate dau același număr. Un pătrat magic normal conține toate numerele de la 1 la n2, iar careuri magice de acest gen există pentru n≥1, exceptând n=2. Cazul n=1 este banal, careul având doar o căsuță în care este înscrisă cifra 1. Cel mai mic ordin "interesant" al unui careu magic este 3, un exemplu fiind careul de mai jos.
Suma constantă de pe fiecare linie, coloană sau diagonală se numește sumă magică și depinde numai de valoarea n, ea putând fi calculată astfel: Careurile magice au o istorie îndelungată, fiind prezente într-o multitudine de variante, pe toate continentele Terrei. De aceea sunt considerate cele mai cunoscute elemente de matematică recreativă.
Mai jos, exemple de careuri magice din timpul romanilor, asociate fiecărei planete.
calculeaza primul tabel !!!
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Jocuri matematice[modificare | modificare sursă]
Jocurile matematice se diferențiază de puzzle-uri prin faptul că există doi sau mai mulți jucători. În ceea ce privește jocurile cu doi adversari, acestea sunt diferite de jocurile obișnuite prin simplul fapt că jocul în sine este reprezentat mai mult de analiza posibilităților etc. Jocurile care utilizează numere nu intră în această categorie și de aceea sunt denumite puzzle-uri.
Matematica jocului[modificare | modificare sursă]
Deși sunt numite jocuri și nu necesită un grad mare de cunoștințe matematice, nu sunt și o joacă de copil. Tehnici de strategie avansate și explicații teoretizate intens transformă jocurile matematice într-un domeniu important din punct de vedere științific. Fiecare joc prezentat mai jos are aplicații în diverse teorii sau teoreme.
Printre acestea se numără:
- Teoria jocurilor
- Teoria combinatorică
- Teoria grafurilor
- Teoria grupurilor
- Teoria lui Ramsey
- Teorema Sprague-Grundy

Se poate afirma astfel că jocurile au un substrat foarte serios și o bază teoretică de obicei bine pusă la punct.
Exemple[modificare | modificare sursă]
Șah[modificare | modificare sursă]
Jocul se desfășoară pe tabla de șah; aceasta are o formă pătrată și este împărțită în 8 linii, numite orizontale și 8 coloane, numite verticale ce formează 64 de pătrate cu suprafețe egale, numite câmpuri colorate alternativ în alb și negru. La început fiecare jucător are 16 piese: 8 pioni, 2 turnuri, 2 cai, 2 nebuni, un rege și o regină. Un jucător controlează piesele albe iar celălalt piesele negre. Jucătorii mută pe rând, respectând anumite reguli. Scopul jocului este obținerea matului. Acesta survine atunci când un rege este atacat și nu poate fi mutat nicăieri spre a evita capturarea.

Chomp[modificare | modificare sursă]
Cei mai mulți își aduc aminte de PacMan Chomper. Chomp este un joc care are ca bază o tablă cu mai multe elemente și fiecare jucător trebuie să "mănânce" elemente pe linie sau pe coloana, până când nu mai ramane nimic. Cine "mănâncă" ultima piesa pierde.

Dots[modificare | modificare sursă]
Tabla de joc este formată dintr-o grilă dreptunghiulară de puncte. Fiecare jucător trebuie să unească cu o linie orizontală sau verticală două dintre punctele pe grilă. Scopul este să formeze pătrățele cu latura de o unitate. Jucătorul care trasează a patra latură a unui astfel de pătrat primește un punct și trebuie să mai facă o mutare.
Jocul se termină atunci când toate mișcările s-au epuizat și nu mai pot fi unite puncte de pe tabla de joc. Câștigător este cel care a acumulat cele mai multe puncte.
Grila poate fi de orice dimensiune, de la foarte mici (ca cea din imaginea alăturată) până la foarte mari (de exemplu, 50x50). Începătorii de obicei fac mutări la nimereală până când în grilă mai sunt numai "lanțuri", o succesiune de spații care au punctele de pe laterală unite, lățimea de o casuță iar la un capăt sunt închise, ceea ce determină o completare în lanț a pătrățelelor.

Un jucător avansat însă dacă va fi pus în fața unui lanț pe care completându-l, ar trebui sa deschidă un alt lanț de dimensiuni mai mari pe care astfel l-ar completa adversarul său, va adopta o altă strategie și anume nu va completa lanțul ci va "ceda" ultimele două puncte adversarului, trasând linia cu o casuță după celula de început, obligându-și partenerul să deschidă el următorul lanț (așa cum este prezentat în figură).
Prin prisma teoriei combinatorice a jocurilor, acest joc poate fi analizat folosind teorema Sprague-Grundy.
Go[modificare | modificare sursă]
Joc pur de inteligență, mai complex și se spune adesea, mai interesant decât toate celelalte jocuri, Go-ul este în același timp unul dintre cele mai vechi sporturi ale minții practicate de om. Istoria sa începe cu aproximativ două milenii înaintea erei noastre, în China, fiind inventat, după unele cronici, de împăratul Shun, ca mijloc de accelerare a dezvoltării minții nu tocmai strălucite a fiului său, după alte cronici, mai credibile, de un vasal al împăratului Kich Kwei, pe nume Wu, același care a inventat și cărțile de joc. La începutul erei noastre, jocul cunoștea o mare dezvoltare în China, apoi, in jurul anului 735 e.n., a trecut în Japonia unde în câteva secole a fost adus la perfecțiune. Ținut la mare cinste la curțile nobiliare, cu numeroși jucători faimoși, de numele cărora sunt legate partide istorice, cu miză uriașă (se pare că, uneori, conflicte militare propriu-zise erau decise în urma unor întâlniri mai puțin sângeroase, dar nu mai puțin înverșunate, în jurul tablei de GO), nelipsit din echipamentul războinicilor vremii, cu o Academie de GO protejată de shogun și beneficiind de cei mai buni profesori, de la introducerea în Japonia și până la jumătatea secolului trecut jocul cunoaște o continuă evoluție ascendentă (atât în conținut cât și ca prestigiu).
Calitățile GO-ului sunt incontestabile și cel mai pregnant mod de a le scoate in evidență este comparația cu șahul, alt joc care face cinste inteligenței umane, dar care, deși mult mai răspândit astăzi decât GO-ul, este depășit de acesta din urmă din mai multe puncte de vedere.
Se spune adesea despre GO ca regulamentul poate fi învățat în 5 minute, tactica și strategia sa în 30 de ani.
Au fost susținute teze de doctorat în economie bazate pe analogia cu GO-ul.Încercările de abordare din punctul de vedere al programatorilor s-au lovit de mari dificultăți, începând chiar de la studiul pe table 3x3, atunci când s-a încercat examinarea arborelui complet al jocului contând pe "forța brută" a computerului (aceasta se întâmpla prin anii 1963-1964). Complexitatea este subliniată, de exemplu, prin estimarea numărului total de configurații posibile pe tabla de GO: acesta este aproximativ 3361 (deoarece avem 19x19=361 de intersecții, iar fiecare intersecție se poate afla în 3 stări: liberă, ocupată de o piesă albă sau ocupată de o piesă neagră). În anul 1986, compania Multitech Industrial Corporation a lansat un premiu de 1 milion de dolari pentru primul program pe computer care să fie capabil să joace GO la nivel "dan"; oferta urma să rămână deschisă până în anul 2000.
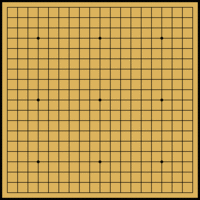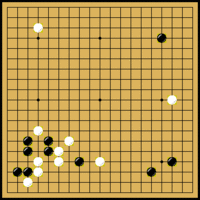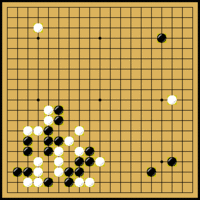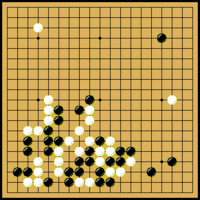
Go-ul se joacă pe o tablă caroiată prin 19 linii orizontale și 19 linii verticale cu piese albe și negre de formă lenticulară identică numite pietre (181 negre și 180 albe). Ca și la șah, liniile verticale se notează cu litere (A,B,C,D,E,F,G,H,J,K,L,M,N,O,P,Q,R,S,T - lipsește I din cauza asemănării cu cifra 1) iar cele orizontale cu numere (de la 1 la 19). Punctele D4, D10, D16, K4, K10, K16, Q4, Q10 și Q16 sunt îngroșate fiind folosite pentru plasarea pieselor handicap.

Cei doi jucători plasează pe rând câte o piesă pe tablă, într-un punct de intersecție a două linii. Piesele nu-și schimbă niciodată locul. Jucătorul cu piesele negre mută primul. Dacă diferența de tărie între jucători este mare, atunci jucătorul mai slab poate primi între 2 și 9 piese handicap, piese care se așează în acele puncte de handicap.
Punctele adiacente unei piese se numesc libertăți. O piesă izolată are 4, 3 sau 2 libertăți, în funcție de poziție (în centrul tablei, pe o linie de margine sau la un colț de tablă). O piesă sau un grup de piese încercuit de adversar astfel încât mai are o singură libertate se numește în atari. Dacă nu mai are nicio libertate este capturat iar piesele se ridică de pe tablă.
Pentru mai multe detalii, vezi articolul despre Go.
Hex[modificare | modificare sursă]
Hex este un joc popular jucat pe o suprafață grilată hexagonală, teoretic de orice mărime sau formă, însă în mod tradițional, Hex se joacă pe o tablă romboidă de dimensiuni 11 x 11. Alte dimensiuni populare sunt 13 x 13 și 19 x 19, ceea ce duce cu gândul la jocul GO. Conform cărții ‘’A beautiful mind’’ , John Nash, inventatorul jocului, considera că dimensiunea 14 x 14 era optimă
Hex a fost inventat de matematicianul danez Piet Hein care a prezentat jocul în 1942 la Institutul Niels Bohr. În mod independent a fost inventat și de John Nash in 1947 la Universitatea Princeton. În Danemarca a devenit cunoscut sub numele de ‘’Polygon’’ (deși Hein îl numise CON-TAC-TIX). Colegii de joc ai lui Nash au denumit simplu jocul după inventatorul lui iar in 1952 Parker Brothers au scos pe piață o versiune a jocului numind-o HEX iar numele a rămas așa.
Joc de strategie, face parte din seria jocurilor de conexiune, tot in această categorie intrând și Omni, Y, Havannah, toate acestea fiind în relație strânsa cu Go. Versiunea lui Nash a jocului era concepută ca o continuare firească a celebrului joc asiatic.

Fiecare jucător are o culoare, roșu sau albastru fiind convenționale. Jucătorii plasează pe rând câte o piatra de culoarea aleasă pe o singură celulă de pe tabla de joc. Scopul este să formeze un drum între două fețe opuse ale tablei de joc, alăturând piese de aceeași culoare. Primul care unește cele doua laturi este cel care caștigă. Primul jucător are în general un avantaj clar prin faptul că poate să-și aleagă punctul de început, de aceea regulamentul spune că al doilea jucător poate să aleagă să facă schimb de poziții cu primul după ce acesta a făcut prima mutare.
Jocul L (BONOL)[modificare | modificare sursă]

În 1969 apărea la editura londoneză Pelican cartea ‘’Cursul de gândire în cinci zile’’ de Edward de Bono, în care printre altele era introdus și un joc logic inedit și atrăgător. Autorul îl numea ‘’’jocul L’’’.
Jocul se practică pe o tablă pătrată caroiată 4 x 4. Fiecare dintre cei doi jucători are câte o literă L (de culori diferite, una neagră și una albă, de exemplu) formată din patru pătrățele. Există, de asemenea, două piese mici neutre (de culoare gri). Inițial, cele patru piese sunt așezate ca în figura alăturată. Apoi, jucătorii mută pe rând, o mutare constând în ridicarea L-ului propriu de pe tablă și plasarea lui în altă poziție, într-un loc liber, desigur (este permisă și întoarcerea cu cealaltă față in sus), urmată eventual și de mutarea unui pătrat gri. Câștigator este jucătorul care îl aduce pe adversar în situația de a nu mai putea muta.
Există în total 2 296 de configurații distincte ale celor patru piese. Dintre acestea, considerând că negrul este la mutare, 15 sunt poziții în care partida este deja încheiată în favoarea albului; din alte 14 poziții, albul bate sigur (dacă joacă perfect bineînțeles) în 2, 4, 6 sau cel mult 8 mutări. În schimb, jucând corect și fiind la mutare, negrul poate învinge în 1006 poziții. Restul de 1261 de configurații conduc la remiză prin ciclare.
Nim[modificare | modificare sursă]
Nim este un joc matematic de strategie în care jucătorii îndepărtează pe rând obiecte din grămezi diferite. La fiecare mutare, un jucător trebuie să îndeparteze măcar un obiect putând îndepărta oricâte obiecte atât timp cât fac parte din aceeași grămada.
Variante ale jocului au fost jucate înca din Antichitate. Se spune că țara sa de origine este China (seamănă foarte mult cu jocul chinezesc Jiashizi) dar originea sa rămâne incertă. Cele mai noi referiri europene la Nim datează de la începutul secolului XVI, iar numele său a fost dat de către Charles L. Bouton de la Universitatea Harvard (cel care a finalizat și teoria jocurilor în 1901), însă numelui nu i s-a atribuit nicio explicație. Cel mai probabil numele derivă din termenul german “nimm!” care înseamnă “ia!” . Unii atrag atenția asupra faptului că rotind NIM la 180° spre stânga, se obține WIN.
De obicei, la Nim, jucătorul care ia ultimul obiect pierde, dar mai poate fi jucat și ca un joc normal, ceea ce înseamnă că persoana care face ultima mutare (cel care ridica ultimul obiect) câștiga partida. Cele mai multe jocuri urmează această convenție de joc ‘’normal’’ deși de obicei Nim reprezintă o excepție de la regulă.
Jucat în mod normal, Nim aparține teoremei Sprague-Grundy. O versiune a jocului Nim are o importanță simbolică în filmul “Last Year at Mariebad”(1961)
Sim[modificare | modificare sursă]

Sim se joacă în doi, un jucător roșu și un jucător albastru pe o tabla de joc ce constă în 6 puncte, fiecare punct fiind unit cu celelalte printr-o linie.
Cei doi jucători colorează pe rând orice linie necolorată. Un jucător colorează în roșu si celălalt colorează în albastru, fiecare încercând să evite crearea de triunghiuri formate exclusiv din culoarea lor. Jucătorul care completează un astfel de triunghi pierde.
Teoria lui Ramses ne arată ca niciun joc de Sim nu se poate termina la egalitate.
Căutarile computerizate au verificat faptul că al doilea jucător poate câștiga dacă are un joc perfect însă găsirea unei strategii fără greșeală pe care mintea umană să o poată memora reprezintă încă o problema.
Puzzle-uri matematice[modificare | modificare sursă]
Sau jocuri de o singură persoană, vezi și puzzle. Printre cele mai cunoscute se numără:
Tangram[modificare | modificare sursă]

Printre jocurile logice fascinante ale căror origini trebuie căutate in China Antică, Tangramul ocupă o poziție specială. Joc-jucărie, conceput pentru a fi practicat de o singură persoană, Tangramul este ilustrarea perfectă a aforismului "Maeștrii se dovedesc în lipsa mijloacelor". Într-adevăr, resursele inițiale ale jocului sunt extrem de reduse: șapte figuri geometrice (5 triunghiuri (de diferite mărimi), un pătrat și un paralelogram).
Jocul constă în așezarea celor 7 figuri (toate și numai ele - prima regulă), una lângă alta, fără suprapuneri (a doua regulă), în plan (regulă implicită), pentru a forma anumite figuri date, figuri cu valoare estetică sau imagini stilizate de obiecte reale.
Cele 7 figuri inițiale - se mai numesc și tanuri - provin din decuparea într-un anume fel a unui pătrat, ca în figură. Ele erau confecționate în mod tradițional din piatră, os, lut sau alte materiale "clasice", însă azi pot fi din plastic, lemn, sau alte materiale "moderne".
Legat de Tangram s-a pus întrebarea: Câte figuri convexe pot fi realizate cu ajutorul celor 7 piese? Una este pătratul de plecare, alte 12 sunt prezentate în figura alăturată. Abia în 1942 s-a demonstrat că numai aceste figuri convexe pot fi realizate folosind regulile menționate mai sus, demonstrația fiind făcută de matematicienii Fu Traing Wang și Chuan Chih Hsing, de la Universitatea Națională din Chekiang, China.

Cubul SOMA[modificare | modificare sursă]

Tangramul este inepuizabil nu numai la nivelul combinațiilor posibile cu cele șapte tanuri ci și în ceea ce privește mulțimea jocurilor în care pot fi descoperite trăsături ale sale. Cubul SOMA, inventat de fizicianul și scriitorul danez Piet Hein (autorul și al jocului HEX).
Avem la dispoziție 7 piese formate din câte 3 sau 4 cubușoare unitare, nu orice fel de piese ci toate cele care pot fi formate astfel încât rezultatul să nu fie convex. Exista 7 piese care se pot obține astfel, una singură cu 3 cuburi și șase cu câte 4. Deși piesele sunt obținute în acest mod, fără a fi dinainte "aranjate" astfel încât lucrurile să iasă bine, cu ele poate fi rezolvată următoarea problemă naturala: realizarea unui cub de dimensiuni 3x3x3.
Există exact 240 de soluții diferite ale problemei și au fost obținute de către Conway in 1981. O încercare mult mai dificilă este realizarea unui cub 5x5x5, folosind un cub 2x2x2 um paralelipiped 2x2x1, trei paralelipipede 2x4x1.
Cubul SOMA este folosit nu numai în sensul problemei anterioare, a realizării unui cub 3x3x3 ci și în sensul Tangramului, pentru a realiza dierite construcții cu cele 7 piese.
-
Cubul SOMA
-
Construcţie SOMA (catel cu os in gura)
-
Construcţie SOMA (scaun)
Cubul lui Rubik[modificare | modificare sursă]

Este, poate, cel mai faimos puzzle. Un cub de plastic de câțiva centimetri, secționat pe fiecare direcție în câte trei "felii" astfel încât să se obțină 27 cuburi mai mici, dintre care numai 26 sunt vizibile. Fiecare față este colorată altfel decât celelalte și se poate roti în jurul axului ei central. Rotind de câteva ori la întâmplare feliile cubului, culorile "difuzează" rapid, pierzându-se într-un mozaic aparent incontrolabil în care numai cuburile din centrul fețelor mai amintesc de culoarea inițială.
Revenirea la ordinea inițială pare o speranță irealizabilă: există peste 43 miliarde de miliarde de configurații. Epidemia a fost pregatită în 1975 când un tânăr arhitect maghiar, Erno Rubik, a brevetat o jucărioară multicoloră, menită să-i folosească drept material didactic pentru întărirea intuiției spațiale a studenților săi. În 1978, un amic a lui Rubik ia cubul cu el la Congresul de matematică de la Helsinki și astfel cubul ajunge pe mâna matematicienilor. Cubul a trecut din mână în mână, s-a făcut legătura cu teoria grupurilor (de permutări)
Virusul s-a răspândit cu repeziciune în Franța și Marea Britanie, a trecut apoi oceanul spre America și Japonia, a intrat în atenția unor coloși ai industriei și comerțului cu jucării astfel încât în 1980, grupul Ideal-Toy comanda Ungariei 6 milioane de cuburi.
Dominoul lui Rubik[modificare | modificare sursă]
Inventat tot de Erno Rubik, domino-ul magic este format din 9 cubușoare negre si 9 albe, marcate de la 1 la 9 cu puncte ca piesele de domino și legate pentru a forma doua etaje dintr-un cub. Orice felie poate fi rotită, cea de sus și cea de jos . Problema? Refacerea ordinii de la 1 la 9 punctelor inscrise pe cubușoare atât pe fața albă cât și pe cea neagra, după amestecarea arbitrara a acestor cuburi. Încercarea este mai ușoară decât în cazul cubului (există "numai" 406 125 600 de configurații posibile). Faptul ca feliile laterale nu pot fi rotite decât cu multipli de 180° face inaplicabile majoritatea formulelor cunoscute de la cub.
Exista mai multe metode de rezolvare, unele mai simple altele mai complicate, un algoritm simplu urmand 3 etape:
- separarea cubușoarelor de colț (cele marcate cu 1,3,7 sau 9 puncte) albe de cele negre (centrele fețelor fiind fixe, ele precizează culoarea fețelor)
- punerea cubușoarelor de colț la locul lor, în cadrul fiecărei fețe (1 la nord-vest, 3 la nord-est etc.)
- ducerea cubușoarelor de mijloc la locul lor
Solitarul (peg solitaire)[modificare | modificare sursă]
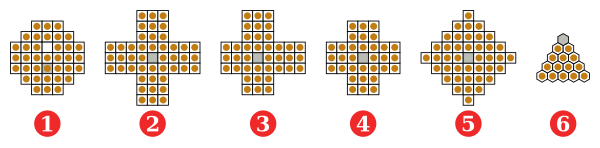
De fapt, sub acest nume sunt cunoscute o serie întreagă de probleme inventate, se spune în secolul XVIII-lea de un conte francez, în timpul unei îndelungi detenții (așa cum consemnează R.C. Bell în Board and table games from many civilizations ) . Toate aceste probleme au ca suport tabla jocului medieval Vulpea și gâștele, pe car sunt așezați pioni identici, în fiecare căsuță câte unul, lăsând una sau mai multe căsuțe libere. Fiecare pion poate sări peste un pion vecin, orizontal sau vertical (nu și pe diagonală, deci), cu condiția ca în spatele acestuia să existe o căsuță liberă. Pionul peste care se sare este eliminat.
Problema "standard" pleacă de la aranjamentul principal și cere ca prin mutări adecvate, să fie eliminați toți pionii, mai puțin unul care să ajungă în final exact în centrul tablei, acolo unde inițial aveam o căsuță libera. Deoarece avem de eliminat 31 de piese, iar la fiecare săritura se elimină una dintre ele, problema poate fi rezolvată în exact 31 de mutări elementare. Numerotând de la 1 la 33 de la stânga spre dreapta, de sus în jos, pe linii, o soluție a problemei este:
Apare ca naturală întrebarea: care este numărul minim de mutări prin care poate fi rezolvată problema inițială a solitarului?
Încă din 1908, H.E. Dudeney a dat o soluție în numai 19 mutări, ilustrată mai sus. Patru ani mai târziu a fost obținută o soluție mai economicoasă, pentru ca exact o jumătate de secol problema să rămână în acest stadiu. În 1962 J.D. Bearey publică în revista "Eureka" Some notes on Solitaire, în car edemonstrează că soluția din 1912 este optimă: nu există nicio posibilitate de rezolvare a problemei solitarului care să folosească mai puțin de 18 mutări.
Poliminouri[modificare | modificare sursă]
Următoarea problemă este aproape nelipsită din cărțile de amuzamente matematice: se ia o tablă de șah și i se elimină două colțuri opuse. Se iau apoi 31 de piese de domino, fiecare egală cu două pătrate ale tablei. Întrebare: pot fi așezate aceste piese (fără suprapuneri) pe tabla astfel trunchiată?
Răaspunsul este nu , cu o justificare pe cât de simplă, pe atât de inteligentă:orice domino acoperă un pătrat alb și unul negru, 31 de dominouri acoperă 31 pătrate albe și 31 negre, dar tabla trunchiată conține 30 de pătrate de o culoare și 32 de cealaltă culoare.
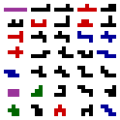
Această problemă i-a inspirat matematicianului american Samuel Golomb o foarte interesantă generalizare, expusă pentru prima dată într-un articol apărut în 1954, în revista The American Mathematical Monthly : Checkers board and polyminoes. Pornind de la faptul că un domino este format din 2 pătrate, deci două mino-uri, el considera și monominouri, triominouri, tetrominouri, pentominouri , în general poliominouri. Terminologia lui Golomb este atractivă însă nu are legătură cu etimologia cuvântului domino, care vine se pare de la latinescul dominus și nu de la do-mino.
-
Hexominouri
-
Pentominouri
-
Tetrominouri
Un poliomino este o figură convexă formată din pătrate vecine pe câte o latură, astfel încât un turn de șah le poate parcurge în întregime.

Problema principală a articolului lui Golomb este acoperirea tablei de șah cu poliominouri de anumite tipuri. Evident este imposibil să acoperim tabla cu triominouri, indiferent de care formă deoarece 64 (numărul pătratelor tablei) nu este divizibil cu 3 (numărul de pătrate dintr-un triomino). Putem însă acoperi tabla de șah cu 21 de triominouri drepte sau în formă de L și un monomino, cu condiția ca în cazul triominourilor drepte, monominoul să ocupe anumite poziții bine precizate. Considerând tetraminourile, tabla de șah poate fi ușor acoperită cu câte 16 piese de tip I, L, T sau O, deoarece și pătratul 4x4 (un sfert de tablă) poate fi acoperit cu asemenea tetrominouri. Referindu-ne la pentaminouri, exista 12 piese distincte și este evident că ele nu pot acoperi complet tabla de șah, dar o pot acoperi împreună cu un tetromino.
Jocurile lui Golomb au fost predecesoarele binecunoscutului Tetris, care nu mai are nevoie de nicio descriere prealabilă.
Sudoku[modificare | modificare sursă]
Joc la modă, Sudoku se joacă pe o grilă 9x9, împărțită în 9 pătrate cu latura de 3 unități. Scopul jocului este de a completa toate căsuțele astfel încât pe fiecare linie și coloană fiecare cifră de la 1 la 9 să nu apară decât o singură dată. Pentru mai multe detalii, vezi Sudoku.
Reprezentanți[modificare | modificare sursă]
Nu puțini au fost pionierii jocurilor matematice. Nume precum Sam Loyd, John Nash, Piet Hein, J.H. Conway, R.K. Guy, M.S. Paterson, Edward Bono se inscriu în galeria personalităților acestui domeniu.
În 1982 a apărut la "Academic Press" o carte monumentală, în două volume de format mare, însumând aproape nouă sute de pagini: Berklekamp, Conway, Guy Winning Ways for your Mathematical Plays , care conținea foarte multe jocuri (abordate matematic), dar în prefața căreia autorii își iau precauția de a recunoaște că (nici măcar) lucrarea lor nu prezintă toate jocurile (logice) cât de cât răspândite. Ea descrie însă numeroase jocuri pe care mulți nu le cunosc.
Au existat (și încă există) reviste de specialitate, printre care amintim de "Rubik's - Logic and Fantasy Dimensions", unde redactor șef era chiar Erno Rubik.
Cei care au contribuit într-un fel sau altul la dezvoltarea acestui domeniu sunt:
-
John Conway
-
Elwyn Berlekamp
-
Richard Guy
-
Lewis Carroll
- John Horton Conway - profesor la Universitatea Princeton
- Elwyn Berlekamp - profesor de matematică la Universitatea California, Berkeley
- Richard Guy - profesor emerit la Universitatea Calgary
- Martin Gardner - scriitor american specializat în matematica recreativă, dar și în pseudoștiință, magie, literatură, filosofie sau religie
- Lewis Carroll - pe numele său adevărat Charles Dogson, scriitor englez, matematician, logician și fotograf, pasionat de jocuri
- Sam Loyd - matematician american, pasionat de jocuri, a rezolvat unele probleme grele de șah, a fost un entuziast al Tangramului dar a și creat jocuri, cel mai faimos fiind jocul 15.
- Ernő Rubik - sculptor ungur, profesor de arhitectură, a creat o multitudine de jocuri, începând din 1974 când aproape din greșeală a oferit lumii fabulosul Cub (vezi mai sus)
- Piet Hein - om de știință danez, a creat jocuri precum HEX sau cubul SOMA.
- Solomon Golomb - matematician, inventatorul poliminourilor, predecesoarele jocului Tetris.
- Douglas Hofstadter - academician american, câștigător al premiului Pulitzer, pasionat de jocuri matematice, autor al unui volum numit Matemagia
-
Sam Loyd
-
Douglas Hofstadter