Trigonometrie

Trigonometria (din limba greacă τρίγωνος trígonos = triunghiular și μέτρον métron = măsură) este o ramură a matematicii care studiază unghiuri, triunghiuri și funcții trigonometrice precum sinusul, cosinusul, tangenta și cotangenta. Unii matematicieni consideră că trigonometria este o subdiviziune a geometriei iar alții un domeniu distinct al matematicii.

Istorie

Originea trigonometriei se consideră a fi în cultura antică din Egipt, Babilon și Valea Indului, acum mai mult de 3000 de ani. Matematicienii indieni au fost pionerii calculului algebric, cu aplicații în astronomie și în trigonometrie. Lagadha e unicul matematician cunoscut care a utilizat geometria și trigonometria pentru astronomie în cartea sa Vedanga Jyotisha, cu toate că multe din lucrările sale au fost distruse de către invadatorii Indiei.

Matematicianul grec Hipparchus a compilat un tabel trigonometric cu valori pentru coarde geometrice asociate unghiurilor din triunghiuri in jurul anului 150 î.Hr. Un alt matematician grec, Ptolemeu (circa 100 î.Hr.) a continuat să dezvolte calculul trigonometric.

Savantul Shia Musulman Nasir al-Din Tusi a fost probabil primul care a considerat trigonometria ca o disciplină matematică distinctă și a fost primul care a descris șase cazuri ale unui triunghi dreptunghic în trigonometria sferică.

Matematicianul de origine sileziană Bartholemaeus Pitiscus a publicat o lucrare importantă în trigonometrie în anul 1595 și a introdus cuvântul în limbile franceză și engleză.

În prezent

Există un număr enorm de aplicații pentru trigonometrie. O importanță specială deține tehnica de triangulație care este utilizată în astronomie pentru a măsura distanța până la stelele apropiate, în geografie pentru a măsura distanțele între repere terestre și în sisteme de satelit pentru navigație (maritimă, în aviație și în spațiul extraterestru). Alte domenii care utilizează trigonometria sunt: muzica, acustica, optica, statistica, biologia, farmaceutica, chimia, oceanografia, ingineria și multe altele.

Funcții trigonometrice

Triunghi dreptunghic.

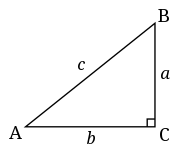
Definiția funcțiilor trigonometrice se bazează pe raporturi între laturi ale unui triunghi dreptunghic plan. Într-un astfel de triunghi, latura cea mai lungă, opusă unghiului drept, se numește ipotenuză, iar laturile care formează unghiul drept se numesc catete.

În triunghiul dreptunghic, sinusul unui unghi ascuțit este definit ca raportul dintre lungimea catetei opuse și lungimea ipotenuzei. Similar, cosinusul unui unghi ascuțit este raportul dintre lungimea catetei alăturate și lungimea ipotenuzei:

$\sin A={{\mbox{cateta opusa}} \over {\mbox{ipotenuza}}}\qquad \cos A={{\mbox{cateta alaturată}} \over {\mbox{ipotenuza}}}$

Valorile unghiurilor cu sinusul/cosinusul rezultat se pot găsi in tabelul valorilor funcțiilor sinus și cosinus.

Acestea sunt cele mai importante funcții trigonometrice; alte funcții pot fi definite ca diferite raporturi ale laturilor unui triunghi dreptunghic, dar pot fi exprimate în termeni de sinus și cosinus. Acestea sunt tangenta, cotangenta, secanta, și cosecanta:

${\mbox{tg}}A={\sin A \over \cos A}={{\mbox{c. o.}} \over {\mbox{c. a.}}}\qquad \sec A={1 \over \cos A}={{\mbox{i.}} \over {\mbox{c. a.}}}$

${\mbox{ctg}}A={\cos A \over \sin A}={{\mbox{c. a.}} \over {\mbox{c. o.}}}\qquad {\mbox{cosec}}A={1 \over \sin A}={{\mbox{i.}} \over {\mbox{c. o.}}}$

Definițiile anterioare se aplică doar la unghiuri între 0 și 90 grade (0 și π/2 radiani). Utilizând cercul unitate (un cerc cu raza de lungime 1) ele pot fi extinse la toate argumentele, pozitive și negative.

Relații trigonometrice

Există o serie de alte relații între elementele (laturi, unghiuri) triunghiurilor oarecare, relații care, folosind funcții trigonometrice, permit calculul unui element necunoscut atunci când se cunosc altele. Astfel de relații sunt de exemplu teorema sinusurilor și teorema cosinusului.

$\sin ^{2}\alpha \ +\cos ^{2}\alpha \ =1$

$\sin \ \alpha \ =\pm \ {\sqrt {1-\cos ^{2}\alpha }}$

${\mbox{tg}}\ \alpha \ ={\sin \alpha \over \cos \alpha }$    $,$ ${\mbox{ctg}}\ \alpha \ ={\cos \alpha \over \sin \alpha }$

$\sin(A+B)=\sin A\cos B+\cos A\sin B\,$

$\cos(A+B)=\cos A\cos B-\sin A\sin B\,$

$\sin(A-B)=\sin A\cos B-\cos A\sin B\,$

$\cos(A-B)=\cos A\cos B+\sin A\sin B\,$

$\tan \alpha =\pm {{\sqrt {1-\cos ^{2}\alpha }} \over \cos \alpha }$

$\sin 2x=2sinxcosx\,$

Teorema sinusurilor

Dacă laturile unui triunghi oarecare sunt a, b și c și unghiurile opuse acestor laturi sunt A, B și C, atunci teorema sinusurilor enunță:

${\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}},$

echivalentă cu:

${\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R$

unde "R" este raza cercului circumscris triunghiului.

Teorema cosinusului

Cu aceleași notații ca mai sus (laturile unui triunghi oarecare: a, b și c, iar unghiurile opuse acestor laturi: A, B și C):

$\cos A={\frac {b^{2}+c^{2}-a^{2}}{2bc}}$

$\cos B={\frac {a^{2}+c^{2}-b^{2}}{2ac}}$

$\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}$

Vezi și

• Tabelul valorilor funcțiilor sinus și cosinus
• Cerc trigonometric

Bibliografie

• Nicolae N. Mihăileanu, Istoria matematicii. Antichitatea și evul mediu, vol I-II, Editura Enciclopedică Română, 1974, 1981

Legături externe

• Materiale media legate de trigonometrie la Wikimedia Commons