Gaură neagră
| Parte a seriei de articole despre | ||||||
| Relativitate generală | ||||||
|---|---|---|---|---|---|---|
 | ||||||
|
Fenomenologie |
||||||
|
Ecuații și teorii
|
||||||

O gaură neagră este o regiune în spațiu-timp cu o forță gravitațională atât de mare încât nimic — nici măcar particulele și radiația electromagnetică ca lumina — nu poate scăpa odată intrat în ea. Teoria relativității generale prezice că o masă suficient de compactă poate deforma spațiul și timpul astfel încât să formeze o gaură neagră. Limitele unei astfel de regiuni din care nimic nu poate scăpa este numită orizontul evenimentelor. Chiar dacă orizontul evenimentelor are un efect enorm asupra sorții și circumstanțele unui obiect care trece prin aceasta, nicio caracteristică aparentă nu poate fi observată. În multe moduri o gaură neagră se comportă ca un corp negru ideal, deoarece nu reflectă lumină deloc. Mai mult, teoria câmpului cuantic în spațiu-timp curbat prezice un orizont al evenimentelor invers proporțional masei acestuia. Temperatura este de ordinul miliardelor de grade Celsius în cazul găurilor negre de masă stelară, făcându-le, esențial, imposibil de observat.[necesită citare]
Obiecte a căror câmp gravitațional sunt suficient de puternice încât lumina nu poate scăpa au fost considerate prima dată în secolul al XVIII-lea de John Michell și Pierre-Simon Laplace. Prima soluție modernă a relativității generale care ar caracteriza o gaură neagră a fost găsită de Karl Schwarzschild în 1916, chiar dacă interpretarea sa ca o regiune din spațiu din care nimic nu poate scăpa a fost prima dată publicată de David Finkelstein în 1958. Găurile negre au fost de mult considerate o curiozitate matematică; a fost în timpul anilor 1960 când munca teoretică a arătat ca acestea au fost o predicție a teoriei relativității generale. Descoperirea stelelor neutron la sfârșitul anilor 1960 au stârnit interes în realitatea obiectelor compacte colapsate gravitațional.
Găurile negre cu o masă stelară sunt așteptate a se forma atunci când o stea foarte masivă se colapsează la sfârșitul ciclului de viață. După ce o gaură neagră s-a format, aceasta poate continua să crească prin absorbția continuă de masă din împrejurimi. Prin absorbția de alte stele și coliziunea cu alte găuri negre, găuri negre supermasive cu o masă de milioane de sori se pot forma. Există o prezumție generală cum că aproape fiecare galaxie are o gaură supermasivă la centrul ei.
În ciuda interiorului invizibil, prezența unei găuri negre poate fi dedusă prin interacțiunea acesteia cu materia și prin radiația electromagnetică cum ar fi lumina vizibilă. Materia care intră într-o gaură neagră poate forma un disc de acreție exterior încălzit de frecare, formând unele dintre cele mai luminoase obiecte din univers. Dacă există alte stele care orbitează o gaură neagră, orbitele lor pot fi folosite pentru a determina masa și locația unei găuri negre. Astfel de observații pot fi folosite pentru a exclude posibilități alternative cum ar fi stelele neutron. În acest fel, astronomii au identificat numeroase găuri negre stelare în sisteme binare, și au stabilit că sursa radio cunoscută sub numele de Sagittarius A*, la centrul propriei noastre galaxii, conține o gaură neagră supermasivă cu o masă aproximativă de 4,3 milioane de sori.
Pe data de 11 februarie 2017, parteneriatul LIGO a anunțat prima detecție a undelor gravitaționale, care reprezintă de asemenea și prima observație a unei fuziuni al unei găuri negre.[1]


Istoria[modificare | modificare sursă]

Ideea existenței unui corp atât de masiv încât nici lumina nu poate scăpa, a fost propusă inițial de către pionierul astronom și clericul englez John Michell într-o scrisoare publicată în noiembrie 1784. Calculele simple ale lui Michell au presupus că un astfel de obiect poate avea aceeași densitate ca soarele nostru, și a concluzionat că un astfel de obiect s-ar forma când diametrul unei stele îl depășește pe cel al soarelui nostru la o scară de 500, și viteza cosmică o întrece pe cea a luminii. Michell a notat corect că astfel de obiecte supermasive dar non-radiante pot fi observate prin studierea efectelor lor gravitaționale asupra obiectelor din vecinătate. Învățații vremii au fost încântați în primă fază de ideea că stele gigant pot apărea ca invizibile, dar entuziasmul s-a stins ușor, odată cu descoperirea în secolul al 19-lea, a faptului că lumina este o undă.
Dacă lumina era o undă în loc de un „crepuscul”, a devenit neclar dacă și ce influență poate avea gravitația asupra razelor de lumină. Relativitatea modernă discreditează noțiunea lui Michell de rază de lumină care se împrăștie direct de pe suprafața unei stele supermasive, fiind încetinită de gravitația stelei, oprită, și apoi eliberată înapoi în cădere pe suprafața stelei.[2]
Relativitatea generală[modificare | modificare sursă]
În 1915, Albert Einstein și-a dezvoltat și publicat teoria relativității generale, arătând anterior faptul că gravitația influențează mișcarea luminii. La scurt timp, Karl Schwarzschild a găsit o soluție la ecuațiile câmpului ale lui Einstein, care descriu câmpul gravitațional al unei mase punct și al unei mase sferice. La câteva luni după Schwarzschild, Johannes Droste, un student al lui Hendrik Lorentz, a dat independent aceiași soluție pentru masa punct și a scris mai pe larg despre proprietățile acesteia. Soluția a avut un comportament ciudat și este ceea ce astăzi este numită Raza lui Schwarzschild, devenind singulară, însemnând că unii dintre termenii din ecuațiile lui Einstein au devenit infiniți. Natura acestei suprafețe nu a fost înțeleasă bine la acea vreme. În 1924, Arthur Eddington a arătat că singularitatea dispare după o schimbare în coordonate (vezi Eddington-Finkelstein coordonate), chiar dacă a trebuit ca Georges Lemaître în 1933 să realizeze că acest lucru înseamnă că singularitatea Razei lui Schwarzschild era o coordonată singulară non-fizică. Arthur Eddington a făcut oarecum un comentariu asupra posibilității unei stele cu o masă compresată la Raza lui Schwarzschild în cartea din 1926, notând că teoria lui Einstein ne permite să conducem peste densități mult mai largi pentru stelele vizibile cum ar fi Betelgeuse deoarece „o stea cu o rază de 250 milioane km nu ar putea să aibă o densitate la fel de mare ca soarele. În primul rând, forța gravitațională ar fi atât de mare încât lumina nu ar putea scăpa, razele căzând înapoi pe suprafața stelei ca rocile pe pământ. În al doilea rând, schimbarea bruscă în liniile spectrale ar fi atât de mare încât spectrul ar fi mutat din existență. În al treilea rând, masa ar produce atât de multă curbare în timp și spațiu încât s-ar închide în jurul stelei, lăsându-ne pe noi înafară” (adică nicăieri).[3][4]
În 1931, Subrahmanyan Chandrasekhar a calculat, folosind relativitatea specială, că un obiect non-rotativ format din materie electron-degenerată asupra unei mase specifice (acum numită limita lui Chandrasekhar la 1.4 M☉) nu are soluții stabile. Argumentele lui au fost respinse de mulți dintre contemporanii lui precum Eddington sau Lev Landau, care au susținut că un mecanism necunoscut încă ar opri colapsarea. Au fost într-o oarecare măsură corecți: o pitică albă cu puțin mai masivă decât limita lui Chandrasekhar s-ar colapsa într-o stea neutron, care este în sine stabilă. Dar în 1939, Robert Oppenheimer și alții au prezis că stelele neutron asupra unei alte limite (limita Tolman-Oppenheimer-Volkoff) s-ar colapsa în continuare din motivele prezentate de Chandrasekhar, și au ajuns la concluzia că nicio lege a fizicii nu ar fi intervenit și ar fi oprit cel puțin unele stele din colapsarea în găuri negre. Calculele lor originale, bazate pe principiul lui Pauli, le-au dat 0.7 M☉; considerații ulterioare a unei forțe repulsive puternice neutron-neutron au crescut estimările la aproximativ 1.5 M☉ până la 3.0 M☉. Observații ale fuziunii stelei neutron GW170817, care se credea a genera o gaură neagră la scurt timp după, au redefinit limitele TOV estimate la 2.17 M☉.
Oppenheimer și co-autorii săi au interpretat că singularitatea la marginile Razei lui Schwarzschild indică că aceasta a fost limitele unei bule în care timpul s-a oprit. Acest punct este unul valid pentru un observator extern, dar nu și pentru cei care cad în gaura neagră. Din cauza acestei proprietăți, stelele colapsate au fost numite „stele înghețate”, deoarece un observator din afară vedea suprafața stelei înghețată în timp în momentul în care colapsul gravitațional a adus-o la Raza lui Schwarzschild
Epoca de aur[modificare | modificare sursă]
În 1958, David Finkelstein a identificat suprafața Schwarzschild ca un orizont al evenimentelor, „o membrană perfect nedirecțională: influențe normale o pot trece doar într-o direcție”. Aceasta nu au contrazis rezultatele lui Oppenheimer direct, dar le-au extins la a include și punctul de vedere al observatorilor care cad în gaura neagră. Soluția lui Finkelstein a extins soluția lui Schwarzschild pentru viitorul observatorilor care cad în gaura neagră. O extensie completă a fost deja găsită de Martin Kruskal, care s-a grăbit s-o publice.[5]
Rezultatele au venit la începutul erei de aur al relativității generale, care a fost marcată de relativitatea generală și găurile negre devenind subiectul principal de cercetare. Acest proces a fost ajutat de descoperirea pulsarilor în 1967, care, până în 1969, au fost arătate a fi stele neutron care se rotesc rapid. Până atunci, stelele neutron, ca găurile negre, au fost categorisite ca curiozități teoretice; dar descoperirea de pulsari au arătat relevanța lor fizică și au sporit interesul în toate obiectele compacte care au putut fi formate printr-un colaps gravitațional.[necesită citare]
În această perioadă mai multe soluții generale la găurile negre au fost găsite. În 1963, Roy Kerr a găsit soluția exactă pentru o gaură neagră rotativă. Doi ani mai târziu, Ezra Newman și colaboratorii săi au găsit o soluție asimetrică pentru o gaură neagră care se și rotește și este și încărcată electric. Prin munca lui Werner Israel, Brandon Carter și David Robinson, a apărut teoria fără-păr, susținând că o soluția unei găuri negre staționare este descrisă complet de cei trei parametri al lui Kerr-Newman: masă, impuls unghiular și încărcătura electrică.
La început, s-a suspectat că caracteristicile ciudate al soluțiilor găurilor negre au fost artefacte patologice de la condițiile simetrice impuse, și că singularitățile nu ar apărea în situații generice. Acest punct de vedere a fost ținut în particular de Vladimir Belinsky, Isaak Khalatnikov și Evgeny Lifshitz, care au încercat să dovedească că nicio singularitate nu ar apărea în soluții generice. Chiar și așa, în anii 1960 Roger Penrose și Stephen Hawking au folosi tehnici globale pentru a dovedi că singularitățile apar generic.[6]
Munca depusă de James Bardeen, Jacob Bekenstein, Carter, și Hawking în 1970 au condus la formularea termodinamicilor găurilor negre. Aceste legi descriu comportamentul unei găuri negre în analogie strânsă cu legile termodinamicii prin relatarea masei cu energia, zona cu entropia și gravitatea suprafeței cu temperatura. Analogia a fost completă când Hawking, în 1974, a arătat că teoria câmpului cuantic prezice că găurile negre ar radia precum un corp negru cu o temperatură proporțională cu gravitatea suprafeței unei găuri negre.
Etimologia[modificare | modificare sursă]
Prima folosire a termenului de „gaură neagră” a fost publicată de jurnalistul ștințific Ann Ewing în articolul ei intitulat „Găuri negre” în spațiu”, datat la 18 ianuarie 1964, care a fost un reportaj la întâlnirea Asociației Americane pentru Avansarea Științei ținută în Cleveland, Ohio.[7][8]
În decembrie 1967, un student a sugerat fraza „gaură neagră” la o lectură de John Wheeler; Wheeler a adoptat termenul pentru propria sa concizie, și a fost prins rapid, lăsându-i pe unii cu acordarea creditului lui Wheeler pentru frază.[9]
Proprietățile și structura[modificare | modificare sursă]

Conjunctura fără-păr postulează că, odată ce aceasta atinge o condiție stabilă după formare, o gaură neagră are doar trei caracteristici fizice independente: masă, încărcătură și impuls unghiular: altfel, gaura neagră este lipsită de caracteristici. Dacă conjunctura este adevărată, oricare două găuri negre care servesc aceleași proprietăți, sau parametri, sunt imperceptibile una de cealaltă. Scara la care conjunctura este adevărată pentru găurile negre reale sub legile moderne ale fizicii, este momentan o problemă nerezolvată.[10]
Aceste proprietăți sunt speciale deoarece sunt vizibile din exteriorul unei găuri negre. Spre exemplu, o gaură neagră încărcată respinge alte încărcături asemănătoare la fel ca orice alt obiect încărcat. Similar, masa totală din interiorul unei sfere care conține o gaură neagră poate fi găsită folosind analogia gravitațională a Legii lui Gauss, masa ADM, departe de o gaură neagră. De asemenea, impulsul unghiular poate fi măsurat departe e o gaură neagră folosind tragerea de cadre din câmpul gravitațional.
Atunci când un obiect cade într-o gaură neagră, orice informație despre forma obiectului sau distribuția încărcăturii de pe acesta este distribuită egal de-a lungul orizontului unei găuri negre, și este pierdută pentru observatorii din afară. Comportamentul orizontului este, în această situație, un sistem disipativ care este aproape analog cu acela al unei membrane conductivă cu frecare și rezistență electrică--paradigma membranei. Acest lucru este diferit de celelalte teorii ale câmpului cum ar fi electromagnetismul, care nu au nicio frecare sau rezistență la un nivel microscopic, deoarece sunt reversibile în timp. Deoarece o gaură neagră atinge, eventual, o stare stabilă cu doar trei parametrii, nu există o cale de a evita pierderea de informații despre condițiile inițiale: câmpurile gravitaționale și de încărcătură ale unei găuri negre dau foarte puține informații despre ce a intrat înăuntru. Informația care este pierdută include orice cantitate care nu poate fi măsurată departe de orizontul unei găuri negre, incluzând numerele conservate cuantic cum ar fi numărul baryon total și numărul lepton. Acest comportament este atât de încurcat încât a fost numit paradoxul informațiilor pierdute al unei găuri negre.[11][12]

Proprietăți fizice[modificare | modificare sursă]
Cele mai simple găuri negre statice au masă dar fie nu au încărcătură electrică sau impuls unghiular. Aceste găuri negre sunt deseori numite ca găurile negre ale lui Schwarzschild după Karl Schwarzschild care a descoperit această soluție în 1916. Conform teoremei lui Birkhoff, este singura soluție care este simetrică sferic. Acest lucru înseamnă că nu există nicio diferență din punct de vedere observațional între câmpul gravitațional al unei astfel de găuri negre și al unui alt obiect sferic cu aceeași masă. Noțiunea populară de gaură neagră care „trage totul înăuntru” este, așadar, doar corect în apropierea orizontului găurii negre; departe, câmpul gravitațional extern este identic cu cel al oricărui corp cu aceiași masă.[13]
Soluții care descriu mai multe găuri negre generale există de asemenea. Găuri negre non-rotative încărcate sunt descrise de către sistemul metric al lui Reissner-Nordstrom, în timp ce sistemul metric al lui Kerr descrie găurile negre ne-încărcate rotative. Cea mai cunoscută soluție pentru găurile negre generale staționare cunoscută sub numele de sistemul metric Kerr-Newmann, care descrie o gaură neagră cu atât încărcătură cât și impuls unghiular.[14]
În timp ce masa unei găuri negre poate avea orice valoare pozitivă, încărcătura și impulsul unghiular sunt constrânse de masă. În unitățile lui Planck, încărcătura electrică totală Q și impulsul unghiular total J sunt așteptate a satisface
pentru o gaură neagră cu o masă M. Găurile negre cu o masă minimă posibilă care satisfac această inegalitate sunt numite extremale. Soluții la ecuațiile lui Einstein care violează această inegalitate există, dar acestea nu posedă un orizont. Aceste soluții au așa-numitele singularități goale care pot fi observate din exterior, de unde sunt numite nefizice. Ipoteza cenzurii cosmice exclude formarea unor astfel de singularități, atunci când sunt create prin colapsul gravitațional al materiei reale. Acest lucru este susținut de simulații numerice.[15]
Din cauza forței relativ mare al forței electromagnetice, găurile negre care se formează din colapsarea stelelor sunt așteptate a reține o încărcătură aproape neutră a stelei. Rotația, oarecum, este așteptată a fi o caracteristică universală a obiectelor astrofizice compacte. Candidatul binar al unei găuri negre cu o sursă X-Ray GRS 1915+105 apare a avea un impuls unghiular aproape de valoarea maximă admisă. Limita neîncărcată este
permițând definiția unui spin nedimensional precum
| Clasa | Aprox. masa |
Aprox. dimensiune |
|---|---|---|
| Gaură neagră supermasivă | 105-1010 MSoare | 0.001–400 UA |
| Gaură neagră cu masă intermediară |
103 MSoare | 103 m ≈ RPământ |
| Gaură neagră stelară |
10 MSoare | 30 km |
| Gaură neagră micro |
până la MLuna | până la 0,1 mm |
Găurile negre sunt deseori clasificate după masa acestora, independentă de impulsul unghiular, J. Mărimea unei găuri negre, după cum este determinată de raza orizontului evenimentelor, sau Raza Schwarzschild, este aproximativ proporțională cu masa, M, chiar dacă
unde rs este raza Schwarzschild și MSoare este masa Soarelui.[16] Pentru o gaură neagră cu rotație nenulă și/sau sarcină electrică, raza este mai mică:
până când o gaură neagră extremă ar putea avea un orizont al evenimentelor aproape de [17]
Orizontul evenimentelor[modificare | modificare sursă]
Caracteristica definitorie a unei găuri negre este aparența unui orizont al evenimentelor -- o limită în spațiu-timp prin care materia și lumina pot trece doar spre centrul masei găurii negre. Nimic, nici măcar lumina, nu poate scăpa din orizontul evenimentelor. Acest orizont este referit în așa fel deoarece dacă un eveniment are loc în interiorul limitei, informația ca un astfel de eveniment s-a petrecut nu poate ajunge la un observator extern, făcând imposibilă determinarea dacă un astfel de eveniment s-a petrecut sau nu.[18]
După cum a fost prezis de relativitatea generală, prezența unei mase deformează timpul și spațiul în așa fel încât calea luată de particule se îndoaie spre masă. La orizontul evenimentelor al unei găuri negre, această deformare devine atâta de puternică încât nu există nicio cale care să meargă într-o altă direcție înafară de gaura neagră.[19]
La un observator distant, ceasurile în apropierea unei găuri negre apar a se mișca mult mai încet decât acestea care sunt mai departe. Din cauza acestui efect, cunoscut și ca dilatare temporală gravitațională, un obiect care cade într-o gaură neagră apare a încetini după cum se apropie tot mai mult de orizontul evenimentelor, având nevoie de un timp infinit pentru a-l ajunge. În același timp, toate procesele care au loc în sau în corelație cu acest obiect încetinesc, din punctul de vedere al unui observator extern, cauzând orice lumină emisă de pe obiect să apară mai roșiatică și mai slab luminată, un efect cunoscut sub numele de diminuare gravitațională. Eventual, obiectul care cade se estompează în depărtare până în punctul în care nu mai poate fi văzut. Tipic, acest proces are loc foarte rapid, în mai puțin de o secundă.[20]
Pe de altă parte, observatorii indestructibili care cad spre o gaură neagră nu sesizează niciun astfel de efect după cum parcurg orizontul evenimentelor. Conform propriilor ceasuri, ce apar a funcționa normal pentru aceștia, parcurg orizontul evenimentelor într-un timp finit fără a experimenta niciun comportament singular; în relativitatea generală clasică, este imposibil a determina locația orizontului evenimentelor din locații observaționale locale, din cauza principiului echivalenței al lui Einstein.[21][22]
Forma orizontului evenimentelor al unei găuri negre este mereu aproximativ sferic. Pentru găurile negre non-rotative geometria orizontului evenimentelor este precis sferică, în timp ce pentru găurile negre rotative orizontul evenimentelor este turtit.[23]
Singularitatea[modificare | modificare sursă]
În centrul unei găuri negre, după cum este descris de relativitatea generală, există o singularitate gravitațională, o regiune unde curbura spațiu-timp devine infinită. Pentru o gaură neagră non-rotativă, această regiune are o formă de un singur punct și pentru o gaură neagră rotativă, forma este impusă a fi un inel care este una cu rotația. În ambele cazuri, regiunea singularități are un volum egal cu zero. Se poate arăta și că regiunea singularității conține toată masa unei găuri negre. Așadar, singularitatea se crede a avea o densitate infinită.[24]
Observatorii care cad într-o gaură neagră Schwarzschild (non-rotativă sau ne-încărcată) nu pot evita tragerea în singularitate, odată ce au trecut orizontul evenimentelor. Aceștia pot prelungi experiența prin accelerarea departe pentru a le încetini coborârea, dar doar până la o limită; odată atinsă o viteză ideală, este cel mai bine căderea liberă în continuare. Atunci când aceștia ating singularitatea, sunt striviți la o densitate infinită și masa lor este adăugată la masa totală al găurii negre. Înainte ca acest lucru să se întâmple, aceștia vor fi rupți în mai multe părți printr-un proces uneori numit și spaghetificare sau „efectul tăiței”, în care diferența gravitațională de la o parte la cealaltă a obiectului este atât de mare încât obiectul este întins până la rupere.[25]
În cazul găurilor negre încărcate (Reissner-Nordström) sau rotative (Kerr), este posibilă evitarea singularității. Extinderea acestor soluții până la maxim arată faptul că există o posibilitate ipotetică de a ieși dintr-o gaură neagră într-un alt spațiu-timp cu o gaură neagră care acționează ca o gaură de vierme. Posibilitatea călătoririi în alt univers este, în orice caz, doar teoretică deoarece orice perturbare ar distruge această posibilitate. De asemenea, se pare că ar putea fi posibilă urmarea unei curbe închise în timp(întoarcerea în trecutul unuia) în jurul singularității lui Kerr, care ar conduce la probleme precum paradoxul bunicului. Este de așteptat ca niciun astfel de efect ciudat nu ar supraviețui în tratamentul cuantic propriu al unei găuri negre rotative sau încărcate electric.[26]
Apariția singularității în relativitatea generală este frecvent percepută ca semnalarea cedării teoriei. Această cedare, în orice caz, este așteptată; apare în situația în care efectele cuantice ar descrie aceste acțiuni, din cauza densității extrem de mare și prin urmare interacțiunii dintre particule. Până azi, nu a fost posibilă combinarea efectelor cuantice cu cele gravitaționale într-o singură teorie, chiar dacă există încercări de a formula o astfel de teorie a gravitației cuantice. Este de așteptat ca o astfel de teorie să nu aibă nicio singularitate.[27][28]
Sfera foton[modificare | modificare sursă]
Sfera foton este o limită sferică de grosime zero în care fotonii care se mișcă pe tangentă cu acea sferă vor fi prinși într-o orbită circulară în jurul găurii negre. Pentru găurile negre non-rotative, sfera foton are o rază de 1.5 ori Raza Schwarzschild. Orbitele lor sunt instabile dinamic, de unde și cea mai mică perturbare, cum ar fi particule ale materiei care cad, ar cauza o instabilitate care ar crește în timp, punând sfera pe o traiectorie în afara găurii scăpând din atracția ei, sau pe o traiectorie în care vor trece, în timp, orizontul evenimentelor căzând în gaura neagră.[29]
În timp ce lumina poate scăpa încă din foto sferă, orice lumină care trece prin foto sferă într-o traiectorie de intrare va fi capturată de gaura neagră. De unde și faptul că orice lumină care ajunge la un observator extern este emisă de obiectele dintre sfera foton și orizontul evenimentelor.
Ergosfera[modificare | modificare sursă]
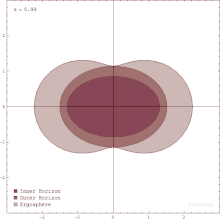
Găurile negre rotative sunt înconjurate de o regiune din spațiu-timp în care este imposibilă statul nemișcat, numită ergosfera. Acest lucru este rezultatul unui proces cunoscut ca tragerea-cadru; relativitate generală prezice că orice masă rotativă tinde să „tragă” ușor de-a lungul spațiului-timp în imediata vecinătate. Orice obiect în apropierea masei rotative va tinde să se miște în direcția rotației. Pentru o gaură neagră rotativă, acest efect este atât de puternic în apropierea orizontului evenimentelor încât un obiect va trebui să se miște mai rapid decât lumina în direcția opusă doar pentru a sta nemișcat.[31]
Ergosfera unei găuri negre este volumul unde limita interioară este orizontul evenimentelor de formă sferică turit al unei găuri negre și o limită exterioară în formă de dovleac, care coincide cu orizontul evenimentelor la poli dar care este notabil mai larg la ecuator. Limita exterioară este uneori numită ergosuprafață.
Obiectele cât și radiația pot scăpa normal din ergosferă. Prin procesul Penrose, obiectele scăpa din ergosferă cu mai multă energie decât au intrat. Această energie este luată de la energia rotativă a găurii negre cauzându-i încetinirea.[32]
Cea mai înaltă orbită circulară stabilă (CÎOCS sau ISCO)[modificare | modificare sursă]
În gravitația Newtoniană, particulele de testare pot orbita stabil la distanțe arbitrare de un obiect central. În relativitatea generală, există o orbită circulară stabilă, în interiorul căreia, orice perturbare oricât de mică orbitei circulare va duce la rotirea acesteia în interiorul găurii negre. Locația acestei orbite depinde de rotirea găurii negre, în cazul unei găuri negre Schwarzschild (rotire zero) este:
și scade după cum rotația găurii negre crește pentru particulele care orbitează în aceeași direcție cu rotația.[33]. Clasificarea completa a orbitelor particulelor cu masa de repaos nenula in campul găurilor negre de tip Kerr- Newman se găsește în tratatul[34]. In cazul celei mai înalte orbite circulare stabile exista o limita a devierii parametrilor mișcării particulei ( moment cinetic, energie), când particula poate forma stări staționare cuantice. In cazul gaurii negre de tip Schwarzschild ISCO va fi stabila atât din punct de vedere a mecanicii clasice, cât și din punct de vedere a mecanicii cuantice pentru gauri negre cu masa M≥10^5-6 Mpl^2/m, unde Mpl este masa planckeana a gaurii negre ~ 10^-5 g [35]
Formarea și evoluția[modificare | modificare sursă]
Dând comportamentul bizar al găurilor negre, a fost de mult pus sub întrebare dacă astfel de obiecte ar putea exista în natură sau dacă acestea sunt soluții patologice la ecuațiile lui Einstein. Einstein în sine a crezut greșit că găurile negre nu se formează, deoarece crezuse că impulsul unghiular al particulelor colapsate ar stabiliza mișcarea acestora la o anumită rază. Acest lucru a dus la comunitatea relativității generale respingând toate rezultatele care arătau contrar timp de mulți ani. În orice caz, o minoritate dintre relativiști au continuat să susțină că găurile negre erau obiecte fizice, și până la sfârșitul anilor 1960, au convins majoritatea cercetătorilor în domeniu că nu există niciun obstacol în formarea unui orizont al evenimentelor.[necesită citare]
Penrose a dovedit că odată ce un astfel de orizont se formează, relativitatea generală fără mecanica cuantică necesită o singularitate să se formeze înăuntru. La scurt timp după, Hawking a arătat că multe soluții cosmologice care descriu Big Bangul au singularități fără câmpuri scalare sau alte forme de materie exotică (vezi „Penrose-Hawking teoremele singularității”). Soluția lui Kerr, teorema fără-păr, și legile termodinamicii unei găuri negre au arătat că proprietățile fizice ale găurilor negre sunt simple și clare, făcându-le subiecte respectate de cercetare. Găurile negre convenționale sunt formate de colapsarea gravitațională a obiectelor masive cum ar fi stelele, dar pot fi formate, în teorie, și de alte procese.
Colapsul gravitațional[modificare | modificare sursă]
Colapsul gravitațional intervine atunci când presiunea internă a obiectului este insuficientă pentru a rezista gravității obiectului în sine. Pentru stele acest lucru apare de obicei atunci când steaua are puțin „combustibil” rămas pentru a-și menține temperatura suficient de mult prin nucleosinteză stelară, sau deoarece o stea care este stabilă primește materie în plus într-un fel în care nu îi ridică suficient temperatura nucleului. În ambele cazuri, temperatura stelei nu este suficient de mare pentru a preveni colapsarea ei sub propria greutate. Colapsul poate fi oprit prin presiunea degenerată de constituenții stelei, permițând condensarea materiei într-o stare mai exotică și densă. Rezultatul este unul dintre multele tipuri variate de stele compacte. Ce tip se formează depinde de masa stelei care a rămas în urma straturilor exterioare care au fost aruncate departe. Astfel de explozii și pulsații duc la nebuloase planetare. Această masă poate fi substanțial mai mică decât masa stelei originale. Resturile care depășesc 5 M☉ sunt produse de stelele care depășeau 20 M☉ înainte de colaps.
Dacă masa stelei rămase depășește 3-4 M☉ (limita Tolman-Oppenheimer-Volkoff), fie din cauza faptului că steaua inițială a fost foarte masivă sau deoarece resturile rămase au colectat masă adițională prin acreția materiei, chiar și degenerarea presiunii neutronilor este insuficientă pentru a opri colapsul. Niciun mecanism cunoscut (cu excepția posibilei presiuni de degenerare „quark”, vezi steaua „quark”) este suficient de puternic pentru a opri implozia obiectului și colapsarea inevitabilă pentru a forma o gaură neagră.

Colapsul gravitațional al stelelor masive este presupus a fi reponsabil pentru formarea găurilor negre cu masă stelară. Formarea stelelor în universul timpuriu ar fi putut rezulta în formarea stelelor super masive, care prin colapsul lor ar fi produs găuri negre cu până la 103 M☉. Aceste găuri negre ar fi putut fi semințele pentru găurile supermasive găsite la centrul celor mai multe galaxii. A fost sugerat mai departe că găurile negre supermasive cu mase tipice de 105 M☉ s-ar fi format din colapsul direct al norilor de gaz în universul timpuriu. Câțiva candidați pentru astfel de obiecte au fost găsite în observațiile asupra universului timpuriu.
În timp ce cea mai multă energie eliberată în timpul colapsului gravitațional este emisă foarte rapid, un observator extern nu observă sfârșitul acestui proces. Chiar dacă colapsul durează o anumită cantitate finită de timp, un observator distant ar vedea materialele care cad și s-ar opri chiar deasupra orizontului evenimentelor, din cauza dilatării gravitaționale a timpului. Lumina de la materialele colapsate durează mai mult și mai mult să atingă observatorul, cu lumina emisă chiar înaintea orizontului evenimentelor având nevoie de o cantitate infinită de timp să ajungă observatorul. Așadar observatorul extern niciodată nu observă formarea orizontului evenimentelor; în schimb, materialele colapsate par a deveni tot mai slab luminate și semnificativ mai roșiatice, eventual disipându-se definitiv.[37]
Găurile negre primordiale și Big Bangul[modificare | modificare sursă]
Colapsul gravitațional are nevoie de o densitate extraordinar de mare. În epoca curentă a universului aceste densități extrem de mari sunt găsite doar în stele, dar în universul timpuriu la scurt timp după Big Bang densitățile erau mult mai mari, posibil permițând formarea găurilor negre. Densitățile mari singure nu sunt suficient de mari pentru a permite formarea unei găuri negre deoarece o distribuție uniformă a masei nu permite adunarea masei într-un singur punct. Ca găurile negre primordiale să se fi putut forma într-un astfel de mediu dens, inițial trebuiau să fie perturbări în densitate care au permis să crească sub propria gravitație. Diferite modele ale universului timpuriu diferă mult în predicțiile acestora cu privire la scara diferitelor fluctuații. Diferite modele prezic formarea găurilor negre primordiale cu mase diferite, de la o masă mică la o masă a sute de mii de mase solare.[38]
În ciuda faptului că universul timpuriu era extrem de dens -- cu mult mai dens decât este necesar pentru ca o gaură neagră să se formeze -- acestea nu s-au re-colapsat într-o gaură neagră în timpul Big Bangului. Modelele colapsului gravitațional al obiectelor cu o mărime relativ constantă, cum ar fi stelele, nu se aplică necesar în același fel cu un spațiu care se extinde rapid precum Big Bangul.[39]
Coliziuni de mare energie[modificare | modificare sursă]

Colapsul gravitațional nu este singurul proces care ar putea crea găuri negre. În principiu, găuri negre se pot forma în timpul coliziunilor de mare energie care ating suficiente densități. Până în 2002, nu au fost detectate astfel de evenimente, fie direct sau indirect prin deficiența balanței masei în experimentele la acceleratorul de particule. Acest lucru sugerează că ar trebui să fie o limită mai mică pentru masa găurilor negre. Teoretic, această limită este așteptată a fi în jurul masei Planck: (mP=√ħ c/G
≈ 1.2×1019 GeV/c2 ≈ 2.2×10−8 kg), unde efectele cuantice sunt așteptate a invalida predicțiile relativității generale. Acest lucru ar pune formarea găurilor negre să nu fie posibilă în urma oricărui proces de mare energie care apare pe sau în apropierea Pământului. În orice caz, anumite dezvoltări în gravitația cuantică sugerează că masa Planck ar putea fi mult mai mică: unele scenarii spre exemplu pun limita la fel de jos ca 1 TeV/c2.[40] Acest lucru ar face imaginabilă crearea micro găurilor negre în coliziunile de mare energie atunci când razele cosmice lovesc atmosfera Pământului, sau posibil în Marele Accelerator de Hadroni de la CERN. Aceste teorii sunt foarte speculative, și crearea găurilor negre în aceste procese sunt refuzate de mulți specialiști. Chiar dacă micro găurile negre ar putea fi formate, este așteptat ca acestea se vor evapora în 10-25 secunde, lăsând Pământul neafectat.[41]
Creșterea[modificare | modificare sursă]
Odată ce o gaură neagră este formată, aceasta poate continua să crească prin absorția de materie adițională. Orice gaură neagră absoarbe continuu gaz și praf interstelar din imprejurimi. Un proces similar a fost sugerat pentru formarea găurilor negre de masă intermediară găsite în grupurile globulare. Găurile negre se pot fuziona și cu alte obiecte cum ar fi stele sau chiar și alte găuri negre. Acest lucru se crede a fi important, în mod special în creșterea timpurie a găurilor negre supermasive, care ar fi putut fi formate prin agregarea a multe obiecte mai mici. Acest proces a fost propus și pentru originea unor găuri negre de masă intermediară.[42][43]
Evaporarea[modificare | modificare sursă]
În 1974, Hawking a prezis ca găurile negre nu sunt complet negre și că emit o mică cantitate de radiație termală; acest efect a ajuns să fie cunoscut sub numele de Radiația Hawking. Aplicând teoria câmpului cuantic unui fundal static al unei găuri negre, a determinat că o gaură neagră ar trebui să emită particule care arată un spectru al unui corp negru perfect. Odată cu publicarea lui Hawking, mulți alții au verificat rezultatul prin diferite metode. Dacă teoria lui Hawking cu privire la radiația găurilor negre este corectă, atunci găurile negre sunt așteptate a se micșora și evapora după cum trece timpul deoarece acestea pierd masă prin emisia de fotoni și alte particule. Temperatura acestui spectru termal (temperatura Hawking) este proporțională cu gravitatea suprafeței unei găuri negre, care este, pentru o gaură neagră Schwarzschild, invers proporțională cu masa. De unde, găurile negre mari emit mai puțină radiație decât cele mici.[44]
O gaură neagră stelară cu masa de 1 M☉ are o temperatură Hawking de -273.15 °C (zero absolut). Această temperatură este cu mult mai mică decât temperatura de fundal al radiației cosmice care este de 2426.85 °C. Găurile negre cu masă stelară sau mai mare primesc mai multă masă de la radiația cosmică de fundal decât emit prin radiația lui Hawking și așadar vor crește în loc să se micească. Ca acestea să aibă o temperatură Hawking mai mare de 2426.85 °C (și deci să poată să se evapore), o gaură neagră ar trebui să aibă o masă mai mică decât cea a lunii. O astfel de gaură neagră ar avea diametrul mai mic decât o zecime de milimetru.[45]
Dacă o gaură neagră este foarte mică, efectele radiației sunt așteptate a deveni foarte puternice. Chiar și o gaură neagră care este grea comparată cu un om s-ar evapora într-o clipită. O gaură neagră cu masa unei mașini ar avea diametrul de 10−24 m și s-ar evapora într-o nanosecundă, timp în care ar avea o luminozitate de 200 de ori mai mare decât cea a soarelui. Găurile negre cu o masă mai mică sunt așteptate a se evapora mai rapid; spre exemplu, o gaură neagră cu masa 1 TeV/c2 - ar avea nevoie de mai puțin de 10−88 88 secunde pentru a se evapora complet. Pentru o astfel de gaură neagră, efectele gravitației cuantice sunt așteptate a juca un rol important și ar putea ipotetic să facă o astfel de gaură neagră stabilă, chiar dacă dezvoltările curente în gravitația cuantică nu arată acest lucru.[46][47]
Radiația Hawking pentru un obiect astrofizic este foarte mică și așadar ar fi extrem de dificil de a fi detectată de pe Pământ. O excepție posibilă, în orice caz, este o izbucnire de raze gamma emise în ultimul stagiu de evaporare al găurilor negre primordiale. Căutarea după astfel de lumini a fost dovedită un eșec până acum și a oferit limite riguroase cu privire la posibilitatea existării a găurilor negre cu masă mică. Telescopul spațial de căutare a razelor gamma Fermi al NASA lansat în 2008 va continua căutarea acestor izbucniri de radiație gamma.[48]
Dacă găurile negre se evapora prin radiația Hawking, o gaură neagră cu masa soarelui nostru se va evapora în (începând atunci când temperatura radiației de fundal al cosmosului scade sub cea a găurii negre) 1064 de ani. O gaură neagră supermasivă cu masa a 100 miliarde ☉ se va evapora în aproximativ 2×10100 ani.[49] Unele găuri negre monstru din univers sunt prezise a continua să crească până la 1014 în timpul colapsului supergrupurilor de galaxii. Chiar și acestea s-ar evapora într-un timp de până la 10106 ani.[50]
Dovezi observaționale[modificare | modificare sursă]

Prin natura lor, găurile negre nu emit direct nicio formă de radiație electromagnetică alta înafară de ipotetica radiație Hawking, deci astrofizicienii care caută găuri negre se bazează de cele mai multe ori pe observații indirecte. Spre exemplu, existența unei găuri negre poate fi propusă uneori prin observarea interacțiunilor gravitaționale cu obiectele înconjurătoare.[51]
Telescopul orizontului evenimentelor (TOR sau EHT), în orice caz, operaționat de Observatorul MIT Haystack, este o încercare de a observa direct mediul înconjurător imediat al orizontului evenimentelor al Sagittarius A*, gaura neagră supermasivă de la centrul galaxiei noastre, Calea Lactee, și de a produce o imagine siluetă cu aceasta. Prima imagine de acest gen ar putea apărea la începutul anului 2018. În 2015, EHT a reușit să detecteze câmpuri magnetice în imediata vecinătate a orizontului evenimentelor al Sagittarius A*, și chiar deosebirea unor caracteristici al acestuia. Existența câmpurilor magnetice a fost prezisă de studiile teoretice ale găurilor negre.[52][53]
Detecția de unde gravitaționale produse de fuziunea găurilor negre[modificare | modificare sursă]
Pe 14 septembrie 2015, observatorul undelor gravitaționale LIGO a făcut prima observare cu succes din istorie asupra undelor gravitaționale. Semnalul a fost consistent cu predicții teoretice pentru undele gravitaționale produse de coliziunea a două găuri negre: una cu 36 M ☉, și cealaltă cu aproximativ 29 M ☉. Această observație aduce cele mai concrete dovezi pentru existența găurilor negre până astăzi. Spre exemplu, undele gravitaționale sugerează că separația a celor două obiecte produsă de coliziune a fost de doar 350 km (sau de 4 ori Raza Schwarzschild care corespunde maselor respective). Obiectele, deci, trebuiau să fie extrem de compacte, lăsând găurile negre ca singura interpretare plauzibilă.
Mai important, semnalul observat de LIGO a inclus și semnalul post-coliziunii, un semnal produs cum noile obiecte formate compact se așează la o stare staționară. Argumentabil, acest semnal a fost cel mai direct mod de a observa o gaură neagră. De la semnalul LIGO este posibilă extragerea frecvenței și amortizarea sunetului și a modului dominant al semnalului. Prin aceste procese, este posibilă deducerea masei și a impulsului unghiular al obiectului final, care corespunde predicțiilor independente de la simulațiile numerice ale fuziunii. Frecvența și timpul de scurgere al modului dominant sunt determinate de geometria sferei foton, chiar și așa nu se pot exclude posibilele alternative exotice ale găurilor negre care sunt suficient de compacte pentru a avea o sfera foton.
Observarea a oferit de asemenea și prima dovadă observațională pentru existența a găurilor negre stelare binare. Mai mult decât atât, este prima dovadă observațională a unei găuri negre având o masă de 25 M ☉ sau mai mare.[54]
Pe data de 15 iunie 2016, o a doua detecție a undelor gravitaționale de la coliziunea a două găuri negre a fost anunțată. Până în aprilie 2018, șase unde gravitaționale au fost observate a proveni de la coliziunea găurilor negre.
Mișcarea adecvată a stelelor care orbitează Sagittarius A*[modificare | modificare sursă]
Mișcarea adecvată a stelelor în apropierea centrului galaxiei noastre aduc dovezi observaționale puternice că aceste stele orbitează o gaură neagră supermasivă. Din 1995, astronomii au urmărit mișcarea a 90 de stele care orbitează un obiect invizibil care corespunde cu sursa radio Sagittarius A*. Prin ajustarea mișcării lor la orbitele Keplerian, astronomii au dedus, în 1998, că, un obiect cu o masă de 2.6 milioane ☉ ar trebui să fie conținut într-un volum cu o rază maximă de 0.02 ani lumină pentru a provoca mișcarea acestor stele. De atunci, una dintre stele - numită S2 -- a completat o orbită completă. Din informațiile primite de la orbită, astronomii au fost capabili să reajusteze calculele la o masă de 4.3 milioane ☉ și o rază mai mică de 0.0002 ani lumină pentru ca un obiect să cauzeze această orbită stelelor. Limita superioară a mărimii obiectului este prea mare pentru a testa dacă este mai mică decât Raza lui Schwarzschild; oricum, aceste observații sugerează puternic că obiectul central este o gaură neagră supermasivă după cum nu există nicio altă explicație plauzibilă în acest scenariu cu o așa mare masă invizibilă într-un volum așa mic. În plus, există și anumite dovezi observaționale că un astfel de obiect ar poseda un orizont al evenimentelor, o caracteristică unică găurilor negre.[55]
Acreția materiei[modificare | modificare sursă]

Din cauza conservării impulsului unghiular, gazul care cade în atracția gravitațională al unui obiect masiv va forma, tipic, o structură asemănătoare unui disc în jurul obiectului. Impresiile artiștilor despre o gaură neagră cu o coroană (acreția materiei) deseori și greșit reprezintă un obiect într-un spațiu plat (gaură neagră) ascunzând o parte din disc în spatele acesteia, dar în realitate efectul gravitațional asupra obiectului ar distorsiona foarte mult discul acreției.[57]

În interiorul unui astfel de disc, frecarea ar cauza impulsului unghiular de a fi transferat în afară, permițând materiei să cadă mai mult înăuntru, așadar eliberând energie potențială și crescând temperatura gazului.[58]
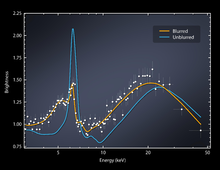
Atunci când obiectul concrescut este o stea neutron sau o gaură neagră, gazul din interiorul discului acreției orbitează la viteze foarte mari deoarece acesta se află în proximitate redusă față de obiectul foarte compact. Frecarea rezultată este atât de semnificativă încât încălzește interiorul discului la temperaturi care emit o vastă cantitate de radiație electromagnetică (în mare parte raze X). Aceste raze X foarte luminoase pot fi detectate de telescoape. Acest proces al acreției este unul dintre cele mai eficiente procese de producere al energiei cunoscut; până la 40% din restul masei materialul acrețit este emis ca radiație. (În fuziunea nucleară doar aproximativ 0.7% din restul masei va fi emis sub formă de energie). În cele mai multe cazuri, discurile de acreție sunt acompaniate de jeturi relativiste care sunt emise de-a lungul polilor, care poartă departe mult mai multă energie. Mecanismul din spatele creării acestor jeturi nu este foarte bine înțeles, în mare parte din cauza lipsei de informații.[59]
Așadar, multe dintre evenimentele mai energetice din univers au fost atribuite acreției materiei în jurul unei găuri negre. În particular, nuclee active galactic și quasari sunt crezuți a fi discuri de acreție a găurilor negre supermasive. Similar, raze X binare sunt general acceptate a fi sisteme binare de stele în car e una dintre cele două stele este mai compactă acrețind materie de la companionul său mai puțin compact. A fost de asemenea sugerat și faptul că unele surse de raze X ultraluminoase ar putea fi discuri de acreție al găurilor negre cu masă intermediară.[60]
În noiembrie 2011 prima observație directă a discului de acreție al unui quasar în jurul unei găuri negre supermasive a fost anunțată.[61][62]
Sisteme de raze X binare[modificare | modificare sursă]

Sisteme binare de raze X sunt sisteme binare de stele care emit o majoritate din radiația lor în spectrumul de raze X. Aceste emisii de raze X sunt crezute a fi rezultatul al unei dintre stele (obiect compact) acrețind materie de la cealaltă stea. Prezența unei astfel de stele într-un astfel de sistem oferă o oportunitate de a studia obiectul central și de a determina dacă este sau nu o gaură neagră.
Dacă un astfel de sistem emite semnale care pot fi urmărite direct înapoi de la obiectul compact, nu poate fi o gaură neagră. Absența unui astfel de semnal poate, în orice caz, a nu exclude posibilitatea ca un obiect compact este o stea neutron. Prin studierea stelei companion este deseori posibil obținerea de parametri orbitale al unui astfel de sistem și de a obține o masă estimată al obiectului compact. Dacă este mult mai mare decât limita Tolman-Oppenheimer-Volkoff (asta este, masa maximă la care o stea neutron poate fi stabilă înainte de a se colapsa) atunci obiectul nu poate fi o stea neutron și este deseori așteptat să fie o gaură neagră.[63]
Primul candidat puternic pentru o gaură neagră, Cygnus X-1, a fost descoperit în acest fel de Charles Thomas Bolton, Louise Webster și Paul Murdin în 1972. Unele suspiciuni, oarecum, rămân din cauza incertitudinii că rezultatul de la steaua companion ar fi mult mai grea decât gaura neagră candidat. Astăzi, candidați mai buni pentru găuri negre sunt găsiți într-un grup de sisteme binare de raze X numit raze X tranzitorii. În această clasă de sistem, steaua companion este de masă relativ mică permițând estimarea mai corectă a masei găurii negre. Mai mult decât atât, aceste sisteme emit activ raze X pe o durată de câteva luni o dată la 10-50 de ani. În această perioadă de emitere a razelor X slabe (numite „quiescence”), discul acreției este mult mai slab luminat permițând observarea detaliată a stelei companion pe durata acestei perioade. Unul dintre cei mai buni astfel de candidați este V404 Cygni.
Fluxul dominant-advecție de acreție și quiescence[modificare | modificare sursă]
Slăbirea discului acreției al unui sistem binar de raze X în perioada quiescence se crede a fi cauzată de fluxul de masă care intră într-un mod numit fluxul dominant-advecție de acreție (FDAA sau ADAF). În acest mod, aproape toată energia generată de frecare în disc este măturată de-a lungul fluxului în loc de a fi radiată departe. Dacă acest model este corect, atunci acesta formează dovezi calitative puternice al prezenței unui orizont al evenimentelor, deoarece dacă obiectul la centrul discului avea o suprafață solidă, acesta ar emite cantități mari de radiația după cum gazul puternic energetic lovește suprafața, un efect care a fost observat la stelele neutron într-o stare asemănătoare.
Oscilații cvasi-periodice[modificare | modificare sursă]
Emisiile de raze X de la discurile de acreție uneori flicăre la diferite frecvențe. Aceste semnale sunt numite oscilații cvasi-periodice și se crede a fi cauzate de materialele care se mișcă de-a lungul marginii interioare al discului de acreție (cea mai înaltă orbită circulară stabilă). Precum frecvența lor este legată de masa obiectului compact. Așadar acestea pot fi folosite ca o alternativă de a determina masa candidatului pentru gaură neagră.[64]
Nucleele galactice[modificare | modificare sursă]

Astronomii folosesc termenul de „galaxie activă” pentru a descrie galaxiile cu caracteristici neobișnuite, cum ar fi linii emisii de linii spectrale neobișnuite și emisii radio foarte puternice. Studii observaționale și teoretice au arătat că activitatea în aceste nuclee galactice poate fi explicată de prezența unei găuri negre supermasive, care poate fi de milioane de ori mai masivă decât cele stelare. Aceste modele consistă în o gaură neagră centrală care poate fi de milioane sau miliarde de ori mai masivă decât soarele nostru; un disc de gaze și praf numit discul de acreție; și două jeturi perpendiculare cu discul de acreție.[65][66]

Chiar dacă găurile negre supermasive sunt așteptate a fi găsite în cele mai multe dintre aceste cazuri, doar unele nuclee galactice au fost mai atent studiate în încercări de a identifica și măsura actuala masă a găurilor negre supermasive. Unele dintre cele mai notabile galaxii cu găuri negre supermasive includ și Galaxia Andromeda, M32, M87, NGC 3115, NGC 3377, NGC 4258, NGC 4889, NGC 1277, JO l 287, APM 08279+5255 și Galaxia Sombrero.[67]
Acum este larg acceptată ideea că centrul al aproape fiecărei galaxii, nu doar cele active, au o gaură neagră supermasivă. Corelația observațiilor apropiate dintre masa acestei găuri negre și dispersia vitezei al găurii galaxiei părinte, cunoscută sub numele de relația M-sigma, sugerează puternic o conexiune între formarea găurilor negre și galaxia în sine.[68]

Microlentile (propus)[modificare | modificare sursă]
O altă metodă prin care natura unei găuri negre al unui obiect poate fi testată în viitor este prin observații ale efectelor cauzate de câmpul gravitațional puternic asupra obiectelor din imediata vecinătate. Un astfel de efect este lentilare gravitațională: deformarea spațiu-timp în jurul unui obiect masiv cauzează razele de lumină să fie deviate foarte mult după cum lumina trece prin lentilele optice. Observații au fost făcute asupra unui astfel de efect doar că la o scară mică, în care razele de lumină au fost deviate doar cu câteva arcsecunde. În orice caz, nu au fost făcute observații directe asupra unei găuri negre. O posibilitate pentru a observa lentilarea gravitațională a unei găuri negre este prin observarea stelelor orbitând o gaură neagră. Există mai mulți candidați pentru o astfel de observare în orbită în jurul lui Sagittarius A*.[70]
Alternative[modificare | modificare sursă]
Dovezile pentru găurile negre stelare se bazează puternic pe existența unei limite superioare pentru masa unei stele neutron. Mărimea acestei limite depinde puternic de presupunerile făcute despre proprietățile materiei dense. Noi faze exotice ale materiei ar putea împinge această legătură. A fază de cuarci liberi la densitate mare ar putea permite existența stelelor cuarc dense, precum unele modele supersimetrice prezic existenta stelelor C. Unele extensii ale modelelor standard presupun existența preonilor ca structuri fundamentale ale cuarcilor și leptonilor, care ar putea forma ipotetic stele preon. Aceste modele ipotetice ar putea explica un anumit număr de observații ale găurilor stelare. În orice caz, poate fi arătat din argumentele relativității generale că orice astfel de obiect ar avea o masă maximă.
Din moment ce densitatea medie al unei găuri negre în interiorul Razei lui Schwarzschild este invers proporțională cu pătratul masei, găurile negre supermasive sunt mult mai dense decât găurile negre stelare (densitatea medie unei găuri negre cu 108 M☉ este comparabilă cu cea a apei). În același timp, fizica materiei care formează o gaură neagră supermasivă este mult mai bine înțeleasă și este o alternativă posibilă pentru explicațiile găurilor negre supermasive care au fost observate. Spre exemplu, găurile negre supermasive ar putea fi modelate de un grup larg de obiecte foarte întunecate. Oricum, astfel de alternative sunt tipic instabile suficient pentru a explica candidații găurilor negre supermasive.
Dovezile pentru existența găurilor negre stelare și supermasive implică că ca o gaură neagră să nu se formeze, relativitatea generală trebuie să cadă ca teorie a gravitației, probabil din cauza corecțiile mecanicii cuantice. O mult anticipată caracteristică a teoriei gravitației cuantice este că nu ar arăta nicio singularitate sau orizont al evenimentelor și așadar o gaură neagră nu ar fi un artefact real. În 2002, mai multă atenție a fost atrasă de modelul „fuzeball” din teoria coardelor. Bazat pe calculele situațiilor specifice în această teorie, sugestia propusă că stagiile individuale generice ale unei găuri negre nu au un orizont al evenimentelor sau o singularitate, dar că pentru un observator astfel de stagii apar ca o gaură neagră obișnuită cum este dedusă din relativitatea generală.[71]
Unele obiecte teoretice au fost presupuse a potrivi observațiilor astronomice ale candidaților pentru găurile negre identice sau aproape identice, dar care funcționează într-un mecanism diferit.[72]
Întrebări deschise[modificare | modificare sursă]
Entropia și termodinamică[modificare | modificare sursă]
În 1971, Hawking a arătat că sub condițiile generale că zona totală a orizontului evenimentelor al oricărei colecții de găuri negre clasice nu poate scădea niciodată, chiar dacă se ciocnesc și se fuzionează. Acest lucru a dus la, ceea ce este astăzi cunoscut sub numele de a doua lege a mecanicii găurilor negre, este extrem de similară cu a doua lege a termodinamicii, care susține că entropia totală a unui sistem nu poate scădea niciodată. Precum obiectele clasice la zero absolut, a fost presupus că găurile negre au zero entropie. Dacă acesta este cazul, a doua lege a termodinamicii ar fi încălcată de materia încărcată entropic care intră într-o gaură neagră, rezultând într-o descreștere a entropiei totale din întreg universul. Așadar, Bekenstein a propus că o gaură neagră trebuie să aibă entropie, și că ar trebui să fie proporțională cu zona orizontului.[73]
Legătură cu legile termodinamicii a fost susținută mai târziu de descoperirea lui Hawkins că teoria câmpului cuantic prezice că o gaură neagră radiază radiație la o temperatură constantă. Acest lucru cauzează o încălcare al legii a doua al mecanismului găurilor negre, deoarece radiația poartă energie departe de gaură neagră cauzând micșorarea acesteia. Această radiație, oricum, poartă departe și entropie, și poate fi dovedită sub asumpție generală că suma totală de entropie al materiei în imediata vecinătate al unei găuri negre și o pătrime din zona orizontului după cum este măsurată în unități Planck este de fapt mereu în creștere. Acest lucru permite formularea primei legi al mecanicii găurilor negre ca un analog la prima lege a termodinamicii, cu masa care acționează ca energie, gravitatea suprafeței ca temperatura și zona ca entropie.
O caracteristică provocatoare este că entropia unei găuri negre este la scară cu zona ei în loc de volum, din moment ce entropia este normal o cantitate extensivă care este la scară lineară cu volumul sistemului. Această proprietate ciudată l-a condus pe Gerard 't Hooft și pe Leonard Susskind să propună principiul holografic, care sugerează că orice care are loc într-un volum spațiu-timp poate fi descris prin informațiile limitei acelui volum.[74]
Chiar dacă relativitatea generală poate fi folosită pentru a folosi o calculație semi-clasică a entropiei unei găuri negre, această situație este teoretic nesatisfăcătoare. În mecanica statisticii, entropia este înțeleasă ca numărarea numărului de configurații microscopice ale unui sistem care are aceleași calități macroscopice (cum ar fi masa, încărcătura, presiunea etc). Fără o teorie satisfăcătoare a gravitației cuantice, nimeni nu poate performa o astfel de simulare pentru găuri negre. Unele progrese au fost făcute în diferite apropieri în relație cu gravitația cuantică. În 1995, Andrew Strominger și Cumrun Vafa au arătat că numărarea microstatică a unei găuri negre supersimetrică în teoria coardelor au reprodus entropia Bekenstein-Hawking. De atunci, rezultate similare au fost raportate pentru diferite găuri negre atât în teoria coardelor cât și în alte abordări ale gravitației cuantice cum ar fi bucla gravitației cuantice.[75]
Paradoxul pierderii informației[modificare | modificare sursă]
Deoarece o gaură neagră are doar câțiva parametri interni, cea mai mare parte din informație legată de materia care a dus la formarea unei găuri negre este pierdută. Indiferent de tipul de materie care intră într-o gaură neagră, se pare că doar informația legată de masa totală, încărcătura și impulsul unghiular sunt conservate. Atâta timp cât găurile negre au fost crezute a persista pentru totdeauna această pierdere a informației nu este atât de problematică, după cum informația nu este pierdută ci ea există în interiorul găurii negre, inaccesibilă din afară, dar reprezentată pe orizontul evenimentelor în concordanță cu principiul holografic. Oricum, găurile negre se evaporă ușor prin emiterea de radiație Hawking. Această radiație nu apare a purta niciun fel de informație adițională legată de materia care a format gaura neagră, ceea ce înseamnă că informația este pierdută pentru totdeauna.[76]
Întrebarea este că fie informația este pierdută pentru totdeauna cu adevărat în găurile negre (paradoxul informației pierdute) a fost divizată într-o comunitate a fizicienilor teoreticieni (vezi pariul Thorne-Hawking-Preskill). În mecanica cuantică, pierderea de informație corespunde cu violarea unei proprietăți vitale numită unitaritate, care este legată de conservarea probabilității. A fost argumentat că pierderea unitarității ar însemna încălcarea și conservării energiei. În ultimii ani dovezi au fost aduse că într-adevăr informația și unitaritatea sunt prezervate într-un tratament gravitațional cuantic al problemei.[77]
Paradoxul firewall[modificare | modificare sursă]
Conform teoriei câmpului cuantic într-un spațiu-timp curbat, o singură emisie de radiație Hawking implică două particule mutuale legate cuantic. Particula care se mișcă spre exterior scapă și este emisă ca un cuantum al radiației Hawking; particula care cade este înghițită de gaura neagră. Presupunând că gaura neagră s-a format în timp finit în trecut și se va evapora complet într-un timp finit în viitor. Atunci, aceasta ar emite doar o cantitate finită de informație reținută în radiația Hawking. Presupunând că la timpul t, mai mult de jumătate din informație a fost deja emisă. Conform studiului acceptat larg de către fizicienii Don Page și Leonard Susskind, o particulă de ieșire emisă la timpul t trebuie să fie legată cu toată radiația Hawking pe care gaura neagră a emis-o precedent. Acest lucru crează un paradox; un principiu numit „monogamie de legătură cuantică” cere ca, precum ca orice sistem cuantic, particula care iese nu poate fi legată cuantic complet cu două sisteme independente la același timp; totuși aici particulare care iese apare a fi legată cuantic cu ambele particule care cad și, independent, cu radiația Hawking.[78]
Pentru rezolvarea acestui paradox, fizicienii s-ar putea, eventual, să renunțe la una dintre cele trei teorii testate în timp: principiul echivalenței al lui Einstein, unitaritatea, sau existența câmpului cuantic. O posibilă soluție, care încalcă principiul echivalenței, este că un „firewall” distruge particulele care vin spre orizontul evenimentelor. În 2016 analiza informațiilor de la LIGO arată semne de ecouri cauzate de un orizont al evenimentelor ciudat; astfel de ecouri pot fi posibile prin teoriile „firewall” sau „fuzzball” dar nu ar trebui să apară în relativitatea clasică generală. În următorii doi ani, informații adiționale LIGO ar trebui să stabilească dacă ecourile au fost doar niște sunete întâmplătoare, sau chiar dacă au fost dovezi ale încălcării relativității generale.
Prima fotografie a unei găuri negre[modificare | modificare sursă]
La data de 10 aprilie 2019 EHT („Event Horizon Telescope“) a prezentat public prima fotografie a unei găuri negre. Gaura neagră se află în interiorul galaxiei superactive Messier 87 (M87), la 55 milioane de ani-lumină de pămȃnt. Pentru realizarea acestei performanțe deosebite 8 telescoape, răspȃndite pe tot globul, au fost cuplate și sincronizate, realizȃndu-se practic un telescop gigantic cu o lentilă de dimensiunea pămȃntului. Observațiile s-au desfășurat pe parcursul anilor 2016,2017, 2018 și 2019, fotografiile fiind asamblate în final cu ajutorul unor aparate speciale într-o imagine unică. Coordonarea celor 8 telescoape s-a făcut sub egida EHT („Event Horizon Telescope“).
Note[modificare | modificare sursă]
- ^ „Detection of gravitational waves”. LIGO. Accesat în .
- ^ Crass, Institute of Astronomy - Design by D.R. Wilkins and S.J. „Light escaping from black holes”. www.ast.cam.ac.uk (în engleză). Accesat în .
- ^ Eddington, Arthur (). The Internal Constitution of the Stars. Cambridge University Press. p. 6. ISBN 9780521337083. Arhivat din originalul de la .
- ^ Kip Thorne comments on this quote on pp. 134–135 Arhivat în , la Wayback Machine. of his book Black Holes and Time Warps, writing that "The first conclusion was the Newtonian version of light not escaping; the second was a semi-accurate, relativistic description; and the third was typical Eddingtonian hyperbole ... when a star is as small as the critical circumference, the curvature is strong but not infinite, and space is definitely not wrapped around the star. Eddington may have known this, but his description made a good story, and it captured in a whimsical way the spirit of Schwarzschild's spacetime curvature."
- ^ Kruskal, M. (). „Maximal Extension of Schwarzschild Metric”. Physical Review. 119 (5): 1743. Bibcode:1960PhRv..119.1743K. doi:10.1103/PhysRev.119.1743.
- ^ Ford, L. H. (). „The Classical Singularity Theorems and Their Quantum Loopholes”. International Journal of Theoretical Physics. 42 (6): 1219. doi:10.1023/A:1025754515197.
- ^ Siegfried, Tom (). „50 years later, it's hard to say who named black holes” (în engleză). Science News. Arhivat din originalul de la . Accesat în .
It seems that the “black hole” label was also bandied about in January 1964 in Cleveland at a meeting of the American Association for the Advancement of Science. Science News Letter reporter Ann Ewing reported from that meeting, describing how an intense gravitational field could cause a star to collapse in on itself. “Such a star then forms a ‘black hole’ in the universe,” Ewing wrote
- ^ Brown, Emma (). „Ann E. Ewing, journalist first reported black holes”. Boston.com. Arhivat din originalul de la . Accesat în .
- ^ Overbye, Dennis (). „John A. Wheeler, Physicist Who Coined the Term 'Black Hole,' Is Dead at 96”. The New York Times. Arhivat din originalul de la . Accesat în .
- ^ Heusler, M. (). „Stationary Black Holes: Uniqueness and Beyond”. Living Reviews in Relativity. 15 (7): 7. arXiv:1205.6112
 . Bibcode:2012LRR....15....7C. doi:10.12942/lrr-2012-7. PMC 5255892
. Bibcode:2012LRR....15....7C. doi:10.12942/lrr-2012-7. PMC 5255892  . PMID 28179837.
. PMID 28179837.
- ^ Anderson, Warren G. (). „The Black Hole Information Loss Problem”. Usenet Physics FAQ. Arhivat din originalul de la . Accesat în .
- ^ Preskill, J. (). Black holes and information: A crisis in quantum physics (PDF). Caltech Theory Seminar. Arhivat (PDF) din originalul de la .
- ^ Seeds, Michael A.; Backman, Dana E. (). Perspectives on Astronomy. Cengage Learning. p. 167. ISBN 978-0-495-11352-2. Arhivat din originalul de la .
- ^ Shapiro, S. L.; Teukolsky, S. A. (). Black holes, white dwarfs, and neutron stars: the physics of compact objects. John Wiley and Sons. p. 357. ISBN 978-0-471-87316-7.
- ^ Berger, B. K. (). „Numerical Approaches to Spacetime Singularities”. Living Reviews in Relativity. 5 (1): 2002–1. arXiv:gr-qc/0201056
 . Bibcode:2002LRR.....5....1B. doi:10.12942/lrr-2002-1. PMC 5256073
. Bibcode:2002LRR.....5....1B. doi:10.12942/lrr-2002-1. PMC 5256073  . PMID 28179859.
. PMID 28179859.
- ^ Wald 1984, pp. 124–125.
- ^ Saa, Alberto; Santarelli, Raphael (). „Destroying a near-extremal Kerr-Newman black hole”. Physical Review D. 84 (2): 027501. arXiv:1105.3950
 . Bibcode:2011PhRvD..84b7501S. doi:10.1103/PhysRevD.84.027501.
. Bibcode:2011PhRvD..84b7501S. doi:10.1103/PhysRevD.84.027501.
- ^ Wheeler 2007, p. 179.
- ^ „Singularities and Black Holes > Lightcones and Causal Structure”. plato.stanford.edu. Stanford Encyclopedia of Philosophy. Accesat în .
- ^ „What happens to you if you fall into a black holes”. math.ucr.edu. John Baez. Accesat în .
- ^ Carroll 2004, p. 222.
- ^ „Watch: Three Ways an Astronaut Could Fall Into a Black Hole”. . Accesat în .
- ^ Shapiro, Stuart (). „Toroidal black holes and topological censorship”. Physical Review D. 52 (12).
- ^ „Sizes of Black Holes? How Big is a Black Hole?”. Sky & Telescope. . Accesat în .
- ^ Wheeler 2007, p. 182.
- ^ Poisson, E.; Israel, W. (). „Internal structure of black holes”. Physical Review D. 41 (6): 1796. Bibcode:1990PhRvD..41.1796P. doi:10.1103/PhysRevD.41.1796.
- ^ Hamade, R. (). „Black Holes and Quantum Gravity”. Cambridge Relativity and Cosmology. University of Cambridge. Arhivat din originalul de la . Accesat în .
- ^ Palmer, D. „Ask an Astrophysicist: Quantum Gravity and Black Holes”. NASA. Arhivat din originalul de la . Accesat în .
- ^ Nitta, Daisuke; Chiba, Takeshi; Sugiyama, Naoshi (septembrie 2011). „Shadows of colliding black holes”. Physical Review D. 84 (6): 063008. arXiv:1106.2425
 . Bibcode:2011PhRvD..84f3008N. doi:10.1103/PhysRevD.84.063008.
. Bibcode:2011PhRvD..84f3008N. doi:10.1103/PhysRevD.84.063008.
- ^ Davoust, Emmanuel. "A hundred years of science at the Pic du Midi Observatory". arXiv:astro-ph/9707201, page 35, Fig. 3
- ^ Carroll 2004, Ch. 6.6.
- ^ Carroll 2004, Ch. 6.7.
- ^ Bardeen, J. M. (). „Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation”. The Astrophysical Journal. 178: 347–370. Bibcode:1972ApJ...178..347B. doi:10.1086/151796.
- ^ Ch. Misner, K.Thorne, J.A. Wheeler, Gravitation, Freeman and Co., N.Y., 1973, capitolul 33, suplimentul 33.5
- ^ Alex Găină, Quantum stability of bound orbits nearest the enter of a Black Hole, Romanian Journal of Physics, vol.39, Nos.9- 10, p.639-644, Bucharest, 1994
- ^ „Artist's impression of supermassive black hole seed”. Arhivat din originalul de la . Accesat în .
- ^ Penrose, R. (). „Gravitational Collapse: The Role of General Relativity” (PDF). General Relativity and Gravitation. 34 (7): 1141. Bibcode:2002GReGr..34.1141P. doi:10.1023/A:1016578408204. Arhivat din original (PDF) la .
- ^ Carr, B. J. (). „Primordial Black Holes: Do They Exist and Are They Useful?”. În Suzuki, H.; Yokoyama, J.; Suto, Y.; Sato, K. Inflating Horizon of Particle Astrophysics and Cosmology. Universal Academy Press. pp. astro–ph/0511743. arXiv:astro-ph/0511743
 . Bibcode:2005astro.ph.11743C. ISBN 978-4-946443-94-7.
. Bibcode:2005astro.ph.11743C. ISBN 978-4-946443-94-7.
- ^ Philip Gibbs. „Is the Big Bang a black hole?”. John Baez. Accesat în .
- ^ Arkani–Hamed, N.; Dimopoulos, S.; Dvali, G. (). „The hierarchy problem and new dimensions at a millimeter”. Physics Letters B. 429 (3–4): 263–272. arXiv:hep-ph/9803315
 . Bibcode:1998PhLB..429..263A. doi:10.1016/S0370-2693(98)00466-3.
. Bibcode:1998PhLB..429..263A. doi:10.1016/S0370-2693(98)00466-3.
- ^ Cavaglià, M. (). „Particle accelerators as black hole factories?”. Einstein-Online. 4: 1010. Arhivat din originalul de la .
- ^ Zwart, S. F. P.; Baumgardt, H.; Hut, P.; et al. (). „Formation of massive black holes through runaway collisions in dense young star clusters”. Nature. 428 (6984): 724–726. arXiv:astro-ph/0402622
 . Bibcode:2004Natur.428..724P. doi:10.1038/nature02448. PMID 15085124.
. Bibcode:2004Natur.428..724P. doi:10.1038/nature02448. PMID 15085124.
- ^ O'Leary, R. M.; Rasio, F. A.; Fregeau, J. M.; et al. (). „Binary Mergers and Growth of Black Holes in Dense Star Clusters”. The Astrophysical Journal. 637 (2): 937–951. arXiv:astro-ph/0508224
 . Bibcode:2006ApJ...637..937O. doi:10.1086/498446.
. Bibcode:2006ApJ...637..937O. doi:10.1086/498446.
- ^ Carroll 2004, Ch. 9.6.
- ^ „Evaporating black holes?”. Einstein online. Max Planck Institute for Gravitational Physics. . Arhivat din originalul de la . Accesat în .
- ^ Giddings, S. B.; Mangano, M. L. (). „Astrophysical implications of hypothetical stable TeV-scale black holes”. Physical Review D. 78 (3): 035009. arXiv:0806.3381
 . Bibcode:2008PhRvD..78c5009G. doi:10.1103/PhysRevD.78.035009.
. Bibcode:2008PhRvD..78c5009G. doi:10.1103/PhysRevD.78.035009.
- ^ Peskin, M. E. (). „The end of the world at the Large Hadron Collider?”. Physics. 1: 14. Bibcode:2008PhyOJ...1...14P. doi:10.1103/Physics.1.14.
- ^ Naeye, R. „Testing Fundamental Physics”. NASA. Arhivat din originalul de la . Accesat în .
- ^ Particle emission rates from a black hole: Massless particles from an uncharged, nonrotating hole, Don N. Page, Physical Review D 13 (1976), pp. 198–206. doi:10.1103/PhysRevD.13.198. See in particular equation (27).
- ^ Frautschi, S. (). „Entropy in an Expanding Universe”. Science. 217 (4560): 593–599. Bibcode:1982Sci...217..593F. doi:10.1126/science.217.4560.593. PMID 17817517. See page 596: table 1 and section "black hole decay" and previous sentence on that page.
- ^ „Black Holes | Science Mission Directorate” (în engleză). NASA. Accesat în .
- ^ Johnson, M. D.; Fish, V. L.; Doeleman, S. S.; Marrone, D. P.; Plambeck, R. L.; Wardle, J. F. C.; Akiyama, K.; Asada, K.; Beaudoin, C. (). „Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*”. Science (în engleză). 350 (6265): 1242–1245. arXiv:1512.01220
 . Bibcode:2015Sci...350.1242J. doi:10.1126/science.aac7087. PMID 26785487. Arhivat din originalul de la .
. Bibcode:2015Sci...350.1242J. doi:10.1126/science.aac7087. PMID 26785487. Arhivat din originalul de la .
- ^ „Event Horizon Telescope Reveals Magnetic Fields at Milky Way's Central Black Hole”. cfa.harvard.edu. . Arhivat din originalul de la . Accesat în .
- ^ Abbott, B. P.; et al. (LIGO Scientific Collaboration & Virgo Collaboration) (). „Astrophysical Implications of the Binary Black Hole Merger GW150914”. Astrophys. J. Lett. 818 (2): L22. arXiv:1602.03846
 . Bibcode:2016ApJ...818L..22A. doi:10.3847/2041-8205/818/2/L22. Arhivat din originalul de la .
. Bibcode:2016ApJ...818L..22A. doi:10.3847/2041-8205/818/2/L22. Arhivat din originalul de la .
- ^ Broderick, Avery; Loeb, Abraham; Narayan, Ramesh (august 2009). „The Event Horizon of Sagittarius A*”. The Astrophysical Journal. 701 (2): 1357–1366. arXiv:0903.1105
 . Bibcode:2009ApJ...701.1357B. doi:10.1088/0004-637X/701/2/1357.
. Bibcode:2009ApJ...701.1357B. doi:10.1088/0004-637X/701/2/1357.
- ^ „NASA's NuSTAR Sees Rare Blurring of Black Hole Light”. NASA. . Arhivat din originalul de la . Accesat în .
- ^ "Short-cut method of solution of geodesic equations for Schwarzchild black hole", J.A. Marck, Class.Quant. Grav. 13 (1996) 393–402.
- ^ McClintock, J. E.; Remillard, R. A. (). „Black Hole Binaries”. În Lewin, W.; van der Klis, M. Compact Stellar X-ray Sources. p. 157. arXiv:astro-ph/0306213
 . Bibcode:2006csxs.book..157M. ISBN 978-0-521-82659-4. section 4.1.5.
. Bibcode:2006csxs.book..157M. ISBN 978-0-521-82659-4. section 4.1.5.
- ^ „What powers a black hole's mighty jets?”. Science | AAAS (în engleză). . Accesat în .
- ^ Winter, L. M.; Mushotzky, R. F.; Reynolds, C. S. (). „XMM‐Newton Archival Study of the Ultraluminous X‐Ray Population in Nearby Galaxies”. The Astrophysical Journal. 649 (2): 730–752. arXiv:astro-ph/0512480
 . Bibcode:2006ApJ...649..730W. doi:10.1086/506579.
. Bibcode:2006ApJ...649..730W. doi:10.1086/506579.
- ^ information@eso.org. „Hubble directly observes the disc around a black hole”. www.spacetelescope.org (în engleză). Arhivat din originalul de la . Accesat în .
- ^ Muñoz, José A.; Mediavilla, Evencio; Kochanek, Christopher S.; Falco, Emilio; Mosquera, Ana María (). „A Study of Gravitational Lens Chromaticity with the Hubble Space Telescope”. The Astrophysical Journal. 742 (2): 67. arXiv:1107.5932
 . Bibcode:2011ApJ...742...67M. doi:10.1088/0004-637X/742/2/67.
. Bibcode:2011ApJ...742...67M. doi:10.1088/0004-637X/742/2/67.
- ^ Celotti, A.; Miller, J. C.; Sciama, D. W. (). „Astrophysical evidence for the existence of black holes” (PDF). Classical and Quantum Gravity. 16 (12A): A3–A21. arXiv:astro-ph/9912186
 . doi:10.1088/0264-9381/16/12A/301.
. doi:10.1088/0264-9381/16/12A/301.
- ^ „NASA scientists identify smallest known black hole” (Press release). Goddard Space Flight Center. . Arhivat din originalul de la . Accesat în .
- ^ Krolik, J. H. (). Active Galactic Nuclei. Princeton University Press. Ch. 1.2. ISBN 978-0-691-01151-6.
- ^ Sparke, L. S.; Gallagher, J. S. (). Galaxies in the Universe: An Introduction. Cambridge University Press. Ch. 9.1. ISBN 978-0-521-59740-1.
- ^ Kormendy, J.; Richstone, D. (). „Inward Bound – The Search For Supermassive Black Holes In Galactic Nuclei”. Annual Review of Astronomy and Astrophysics. 33 (1): 581–624. Bibcode:1995ARA&A..33..581K. doi:10.1146/annurev.aa.33.090195.003053.
- ^ Ferrarese, L.; Merritt, D. (). „A Fundamental Relation Between Supermassive Black Holes and their Host Galaxies”. The Astrophysical Journal Letters. 539 (1): 9–12. arXiv:astro-ph/0006053
 . Bibcode:2000ApJ...539L...9F. doi:10.1086/312838.
. Bibcode:2000ApJ...539L...9F. doi:10.1086/312838.
- ^ „A Black Hole's Dinner is Fast Approaching”. ESO Press Release. Arhivat din originalul de la . Accesat în .
- ^ Bozza, V. (). „Gravitational Lensing by Black Holes”. General Relativity and Gravitation. 42 (9): 2269–2300. arXiv:0911.2187
 . Bibcode:2010GReGr..42.2269B. doi:10.1007/s10714-010-0988-2.
. Bibcode:2010GReGr..42.2269B. doi:10.1007/s10714-010-0988-2.
- ^ Skenderis, K.; Taylor, M. (). „The fuzzball proposal for black holes”. Physics Reports. 467 (4–5): 117. arXiv:0804.0552
 . Bibcode:2008PhR...467..117S. doi:10.1016/j.physrep.2008.08.001.
. Bibcode:2008PhR...467..117S. doi:10.1016/j.physrep.2008.08.001.
- ^ Ball, Philip (). „Black holes 'do not exist'”. Nature News (în engleză). doi:10.1038/news050328-8. Accesat în .
- ^ Wald, R. M. (). „The Thermodynamics of Black Holes”. Living Reviews in Relativity. 4 (1): 6. arXiv:gr-qc/9912119
 . Bibcode:2001LRR.....4....6W. doi:10.12942/lrr-2001-6. PMC 5253844
. Bibcode:2001LRR.....4....6W. doi:10.12942/lrr-2001-6. PMC 5253844  . PMID 28163633.
. PMID 28163633.
- ^ 't Hooft, G. (). „The Holographic Principle”. În Zichichi, A. Basics and highlights in fundamental physics. Basics and Highlights in Fundamental Physics. Subnuclear series. 37. pp. 72–100. arXiv:hep-th/0003004
 . Bibcode:2001bhfp.conf...72T. doi:10.1142/9789812811585_0005. ISBN 978-981-02-4536-8.
. Bibcode:2001bhfp.conf...72T. doi:10.1142/9789812811585_0005. ISBN 978-981-02-4536-8.
- ^ Carlip, S. (). „Black Hole Thermodynamics and Statistical Mechanics”. Physics of Black Holes. Physics of Black Holes. Lecture Notes in Physics. 769. pp. 89–123. arXiv:0807.4520
 . Bibcode:2009LNP...769...89C. doi:10.1007/978-3-540-88460-6_3. ISBN 978-3-540-88459-0.
. Bibcode:2009LNP...769...89C. doi:10.1007/978-3-540-88460-6_3. ISBN 978-3-540-88459-0.
- ^ Hawking, S. W. „Does God Play Dice?”. www.hawking.org.uk. Arhivat din originalul de la . Accesat în .
- ^ Mathur, S. D. (). The information paradox: conflicts and resolutions. XXV International Symposium on Lepton Photon Interactions at High Energies. arXiv:1201.2079
 . Bibcode:2012Prama..79.1059M. doi:10.1007/s12043-012-0417-z.
. Bibcode:2012Prama..79.1059M. doi:10.1007/s12043-012-0417-z.
- ^ Merali, Zeeya (). „Astrophysics: Fire in the hole!”. Nature. pp. 20–23. Bibcode:2013Natur.496...20M. doi:10.1038/496020a. Arhivat din originalul de la . Accesat în .
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
- Black Holes pe In Our Time la BBC. (ascultă acum)
- Stanford Encyclopedia of philosophy: Singularități și Găuri Negre, de Erik Curiel și Peter Bokulich.
- en Black Holes: Gravity's Relentless Pull – Interactive multimedia pe web site-ul despre fizică și astronomie de la Space Telescope Science Institute
- Agenția Spațială Europeană Gaură neagră - vizualizare Arhivat în , la Wayback Machine.
- Întrebări adresate frecvent despre Găurile negre
- Schwarzschild Geometrie
- Hubble-ul










