Mecanica fluidelor numerică


Mecanica fluidelor numerică (MFN),[1] mecanica fluidelor computerizată[2] sau dinamica computerizată a fluidelor[3] (engleză computational fluid dynamics – CFD) este o ramură a mecanicii fluidelor, care folosește algoritmi, metode numerice și computere pentru a modela și a rezolva probleme în care apar curgeri ale fluidelor.
Modelarea se bazează pe rezolvarea unui set de ecuații diferențiale de conservare, completate cu numeroase ecuații suplimentare, modele, adesea semiempirice, pentru tratarea turbulenței, a presiunii, cavitației, schimbului de căldură, a transportului speciilor chimice sau a fazelor disperse (en). Aceste ecuații sunt discretizate prin diferite metode, ca metoda diferențelor finite, a elementelor finite, a volumelor finite sau a elementelor de frontieră. Domeniile de modelat sunt împărțite în părți mici, rezultând rețele de discretizare cu multe noduri. Ecuațiile, scrise pentru fiecare nod, sunt asamblate într-un sistem de ecuații global, care apoi este rezolvat.
Principalul domeniu de aplicare este modelarea curgerilor turbulente sub și supersonice în domeniul aerospațial, însă există numeroase alte domenii în care este utilizată, cum ar fi aerodinamica vehiculelor și construcțiilor, optimizarea proceselor chimice, previziuni meteorologice, prospectări geologice, dispersia noxelor, aplicații medicale[4] sau militare.[5]
Introducere și istoric[modificare | modificare sursă]
Baza teoretică a aproape tuturor modelărilor curgerilor sunt ecuațiile Navier–Stokes,[6] care descriu curgerea unei faze fluide unice. Eliminând în aceste ecuații termenii care descriu viscozitatea, se obține un model mai simplu, ecuațiile lui Euler.[7] Eliminând în continuare termenii care descriu vorticitatea se ajunge la ecuațiile curgerii potențiale.[8] În final, aceste ecuații pot fi liniarizate.
Deoarece prin rezolvare se urmărește obținerea câmpurilor diferitelor variabile în interiorul zonei în care curg fluidele, respectiv modul în care fluidele interacționează cu suprafețele ce delimitează domeniul în care fluidele curg. În acest scop se folosesc computere, ca urmare mecanica fluidelor numerică poate fi considerată și o ramură a proiectării asistate de calculator (engleză computer-aided design – CAD), respectiv a ingineriei asistate de calculator (engleză computer-aided engineering – CAE). Cu cât computerele folosite sunt mai puternice, cu atât soluția obținută este mai precisă, sau timpul ei de obținere mai scurt. Soluțiile oferite de modelare sunt validate prin compararea cu valori măsurate pe standuri experimentale (de exemplu tunele aerodinamice), sau în condiții reale.
Istoric, metodele de simulare numerică au fost concepute pentru rezolvarea ecuațiilor liniarizate ale câmpului potențial. În anii 1930 s-au dezvoltat metode bidimensionale pentru tratarea curgerilor în jurul unui profil aerodinamic, folosind transformarea conformă a unei curgeri în jurul unui cilindru.[9] Apariția calculatoarelor a permis dezvoltarea metodelor tridimensionale. Prima comunicare științifică privind o metodă de rezolvare a ecuațiilor liniarizate a câmpului potențial a fost publicată în 1967 de John Hess și A.M.O. Smith de la Douglas Aircraft.[10] Aceștia au discretizat suprafețele cu panouri, și au dezvoltat o clasă de algoritmi numită metoda panourilor.[11] Metoda lor era simplificată și nu trata curgerile care generau portanță, ca urmare a fost aplicată pentru corpuri de nave și fuzelaje de avion. Prima aplicație a metodei panourilor pentru curgeri portante, Panel Code (A230), a fost descrisă într-o comunicare științifică din 1968 de Paul Rubbert și Gary Saaris de la Boeing Aircraft. Cu timpul s-au dezvoltat mai multe programe pe baza metodei panourilor de către Boeing (PANAIR, A502), Lockheed (Quadpan), Douglas (HESS), McDonnell Aircraft (MACAERO), NASA (PMARC) și Analytical Methods (WBAERO, USAERO și VSAERO). Unele dintre ele (PANAIR, HESS și MACAERO) erau programe „de ordin superior”, care admiteau mai multe singularități ale suprafețelor, în timp ce altele (Quadpan, PMARC, USAERO și VSAERO), „de ordin inferior”, admiteau câte o singură singularitate pe fiecare panou. Avantajul programelor de ordin inferior era că rulau mult mai rapid pe calculatoarele din epocă. Actual, VSAERO a trecut la ordin superior și este cel mai folosit program din această clasă. El a fost folosit la proiectarea mai multor submarine, nave, automobile, elicoptere, avioane, iar mai recent pentru turbine eoliene. Programul geamăn USAERO tratează prin metoda panourilor curgeri nestaționare și a fost folosit la proiectarea trenurilor de mare viteză sau a iahturilor de curse. Aplicația PMARC a NASA este o dezvoltare a VSAERO, iar CMARC este o variantă a sa. Toate aceste programe tratează curgeri neviscoase.
În domeniul bidimensional, metoda panourilor a fost folosită la proiectarea profilelor aerodinamice. Metoda a fost completată cu o parte care trata stratul limită, ceea ce permitea modelarea efectelor viscozității. Profesorul Richard Eppler de la Universitatea din Stuttgart a scris programul PROFIL, sponsorizat parțial de NASA, program care a devenit disponibil la începutul anilor 1980. Aceste a fost urmat în curând de programul XFOIL, scris de profesorul Mark Drela de la Massachusetts Institute of Technology (MIT). Ambele programe, PROFIL și XFOIL, încorporează metoda panourilor bidimensională, cuplată cu tratarea stratului limită. PROFIL folosește pentru proiectarea inverselor profilelor aerodinamice transformarea conformă, în timp ce XFOIL știe pentru proiectarea profilelor și transformarea conformă, și metoda inversă a panourilor.
O etapă intermediară între programele bazate pe metoda panourilor și cele care tratează curgerile potențiale propriu-zise a fost cea bazată pe ecuațiile micilor perturbații transsonice. Cea mai cunoscută aplicație de acest gen este WIBCO, scrisă la începutul anilor 1980 de Charlie Boppe de la Grumman Aircraft.
Cercetătorii s-au orientat spre programe bazate pe ecuațiile câmpului potențial când au constatat că metoda panourilor nu permitea modelarea curgerilor transsonice. Prima descriere a necesității modelării câmpurilor potențiale a fost publicată în 1970 de Earll Murman și Julian Cole de la Boeing. Frances Bauer, Paul Garabedian și David Korn de la Courant Institute (Institutul pentru Mecanica Fluidelor) al Universității din New York (NYU) au scris în acest scop o serie de programe bidimensionale, cel mai important fiind Program H. Acesta a fost dezvoltat sub numele de Grumfoil de Bob Melnik și colectivul său de la Grumman Aerospace. Antony Jameson, provenind de la Grumman Aircraft și Courant Institute al NYU au colaborat cu David Caughey pentru a scrie în 1975 programul FLO22, un program pentru curgeri potențiale tridimensionale. Din acesta au derivat mai multe aplicații, dintre care Tranair (A633) de la Boeing este utilizat și în prezent.
Următoarea etapă a fost ecuațiile Euler, care promiteau o acuratețe mai mare în domeniul transsonic. Metodologia folosită de Jameson în programul său tridimensional FLO57 din 1981 a fost folosită de alții pentru a scrie programe ca TEAM al lui Lockheed și MGAERO al lui IAI/Analytical Methods. MGAERO este unic prin folosirea unei discretizări carteziene, în timp ce majoritatea celorlalte programe foloseau discretizări structurate adaptate după forma corpului (cu excepția programelor CART3D al NASA, SPLITFLOW al Lockheed și NASCART-GT al Georgia Tech.[12] Antony Jameson a scris și el în 1985 programul tridimensional AIRPLANE, folosind o discretizare cu elemente tetraedrice.
În domeniul bidimensional, Mark Drela și Michael Giles, pe atunci studenți la MIT, au scris în 1986 programul ISES Euler (actual un pachet de programe) pentru proiectarea profilelor aerodinamice. Acest program a fost dezvoltat ulterior ca programul MSES, larg utilizat. O variantă a programului MSES este MISES care permite tratarea rețelelor de profile, variantă scrisă de Harold "Guppy" Youngren când era și el student la MIT.
Ultima țintă a programatorilor a fost modelarea pe baza ecuațiilor Navier–Stokes. NASA e elaborat programul bidimensional ARC2D și programele tridimensionale ARC3D, OVERFLOW, CFL3D, care au stat la baza a numeroase aplicații comerciale.
Bazele teoretice ale modelării curgerilor[modificare | modificare sursă]
Rezolvarea unei probleme de mecanica fluidelor presupune parcurgerea mai multor etape: formularea modelului matematic, alegerea unei metode numerice adecvată ecuațiilor, dezvoltarea unui algoritm de calcul numeric, implementarea algoritmului într-un program de calcul, iar în final validarea programului de calcul și evaluarea performanțelor.[13]
Ecuațiile care descriu fenomenele de curgere sunt ecuații diferențiale cu derivate parțiale. În general, ecuațiile pot fi liniare, în care nu apar produse între varibile și derivatele lor, respectiv neliniare, în care astfel de produse apar. După ordinul derivatelor, ele pot fi de ordinul întâi sau de ordinul al doilea. Acestea din urmă sunt cele mai potrivite pentru modelarea curgerilor. Pentru un domeniu bidimensional, în , forma generală a unei astfel de ecuații este forma Sneddon, care asigură continuitatea derivatelor de ordinul întâi și al doilea:[14][15]

unde este funcția de proprietate (care descrie o anumită proprietate).
Corespunzător expresiei ecuațiile se clasifică astfel:[15]
- pentru în ecuații eliptice,
- pentru în ecuații parabolice,
- pentru în ecuații hiperbolice.
Soluția este o suprafață determinată de liniile (curbele) caracteristice. Ecuațiile eliptice se caracterizează prin faptul că nu există linii caracteristice (ele sunt imaginare), perturbațiile se propagă în toate direcțiile, domeniul soluțiilor este unul închis și este necesară precizarea condițiilor la limită la frontierele domeniului modelat (pt. condiții la limită, v. mai jos).[15] Ecuațiile eliptice sunt adecvate de exemplu pentru modelarea curgerii, a conducției termice staționare, a difuziei, a stratului limită, a reacțiilor chimice.[16]
Ecuațiile parabolice se caracterizează prin faptul că există o singură linie caracteristică, perturbațiile se propagă în direcția liniei caracteristice, domeniul soluțiilor este unul deschis și este necesară precizarea unei condiții inițiale și a două condiții la limită.[15] Ecuațiile parabolice sunt adecvate pentru modelarea de exemplu a conducției termice nestaționare.[17]
Ecuațiile hiperbolice se caracterizează prin faptul că există două linii caracteristice, perturbațiile se propagă în direcția acestor linii, domeniul soluțiilor este unul deschis și este necesară precizarea a două condiții inițiale și a două condiții la limită.[15] Ecuațiile hiperbolice sunt adecvate pentru modelarea propagării undelor.[18]
Similar se pot trata și clasifica și ecuațiile pentru un domeniu tridimensional, în
Ecuații de conservare[modificare | modificare sursă]

În modelarea curgerilor se folosesc ecuații de conservare (respectiv de transport) ale proprietăților. Acestea conțin diferiți termeni, care reflectă influența a diferite fenomene.
Ecuația de continuitate[modificare | modificare sursă]
La curgerea fluidelor conservarea masei este absolut necesară. Conservarea masei este descrisă de ecuația de continuitate a cărei formă vectorială este:[19][20][21]
unde este densitatea fluidului, iar este vectorul vitezelor. Pentru fluide incompresibile densitatea poate fi considerată constantă sau în funcție de temperatură, iar pentru fluide compresibile poate fi obținută dintr-o ecuație de stare adițională, de exemplu ecuația de stare a gazului ideal.[22]
[modificare | modificare sursă]
- Articol principal: Ecuațiile Navier-Stokes.
Ecuațiile Navier–Stokes sunt ecuații de conservare a impulsului. Aceste ecuații se bazează pe a doua lege a lui Newton aplicată mișcării fluidului, împreună cu ipoteza că tensiunea fluidului este proporțională cu gradientul vitezei (fluid Newtonian), la care se adaugă gradientul presiunii. Ecuațiile furnizează componentele vitezei unei particule de fluid.
Forma vectorială a acestor ecuații este:[6][23][24]
unde partea stângă a ecuației reprezintă accelerația, și poate fi compusă din efecte dependente de timp și convective, sau, dacă sunt prezente, efectul coordonatelor neinerțiale. Partea dreaptă reprezintă suma tuturor forțelor care acționează asupra volumului de control, precum gradientul de presiune, tensorul tensiunilor () și alte forțe, cum ar fi forța gravitațională.
Importanța termenilor de transport difuziv (viscozitate) este preponderentă pentru fenomenele modelate de ecuații eliptice,[25] respectiv a celor de transport convectiv fenomenelor modelate de ecuații hiperbolice.[26] Cât de bună este implementarea numerică a modelării termenilor convectivi, respectiv difuzivi este reflectată de performanțele aplicațiilor software la rezolvarea unora sau altora dintre probleme.
Ecuația de conservare a energiei[modificare | modificare sursă]
Este nevoie de o ecuație de conservare a energiei dacă se iau în considerare fenomene de schimb de energie, cum sunt cele de schimb de căldură și lucru mecanic, de exemplu încălzirea fluidului în urma disipației viscoase. Ecuația de conservare a energiei se bazează pe primul principiu al termodinamicii. Deoarece practic toate curgerile formează sisteme termodinamice deschise, ecuația folosită este în formă vectorială:[27][28]
unde este entalpia masică, iar este gradientul temperaturii.
Cuplarea viteză-presiune[modificare | modificare sursă]

Câmpul de presiuni la curgerea unui fluid nu rezultă din ecuațiile de conservare, el reiese indirect din ecuația de continuitate și este determinant pentru curgere, apărând în termenii sursă din celelalte ecuații.[29] Pentru calcului câmpului de presiuni se cunosc doi algorimi: SIMPLE și PISO.
La algoritmul SIMPLE (acronim din engleză Semi-Implicit Method for Pressure Linked Equations), elaborat de Dudley B. Spalding și Suhas V. Patankar, se presupune un câmp de presiuni cu care se determină vitezele, iar apoi se corectează câmpul de presiuni utilizând o ecuație de corecție, pe baza vitezelor calculate. Deoarece viteza se determină într-un punct, iar presiunea pe o suprafață, procedura se repetă de două ori, folosind o grilă decalată.[30] Ulterior au apărut variantele SIMPLER (acronim din engleză SIMPLE Revised,[31]) și SIMPLEC (acronim din engleză SIMPLE Completed).[32] Varianta SIMPLER este mai economică, iar varianta SIMPLEC, deoarece ia în considerare toți termenii, furnizează corecții care nu necesită subrelaxare (pt. subrelaxare, v. mai jos), reducând în final efortul de calcul.[33]
Algoritmul PISO (acronim din engleză Pressure Implicit with Splitting of Operators), este o variantă a algoritmului SIMPLE în care corecțiile de presiune sunt calculate de mai multe ori (uzual de 3 ori). Este un algoritm mai potrivit pentru curgerile nestaționare.[34][35]
Modele de turbulență[modificare | modificare sursă]
Curgerile turbulente sunt caracterizate prin câmpuri de viteze fluctuante stocastic. Aceste fluctuații amestecă mărimile transportate: impulsul, energia și speciile chimice. Scara fluctuațiilor se întinde de la cele mai mari, de nivel planetar (ex. turbulența atmosferică), până la cele mai mici, moleculare (microscările Kolmogorov).
Una din abordările posibile este simularea numerică directă a fluctuațiilor. Deoarece fluctuațiile pot fi de scara mică și de frecvență înaltă, efortul numeric de a le calcula direct este disproporționat. O altă abordare este de a folosi modele semiempirice, modele de turbulență cu zero, una sau două ecuații. Altă posibilitate este medierea fluctuațiilor. Se cunosc două metode de mediere: medierea Reynolds și filtrarea. În urma ambelor medieri în ecuațiile de transport apar însă termeni suplimentari, care la rândul lor trebuiesc modelați, deci trebuiesc scrise noi ecuații pentru a rezolva închiderea setului de ecuații (numărul de ecuații trebuie să corespundă cu numărul de necunoscute). Pentru modelarea termenilor suplimentari se folosesc ipoteze simplificatoare.[36].
Simularea numerică directă[modificare | modificare sursă]

Simularea numerică directă (engleză direct numerical simulation – DNS) calculează toate fluctuațiile, în întreaga gamă a scărilor turbulenței, fără a face nicio ipoteză empirică.[37] Aceasta elimină influența modelelor, dar este extrem de consumatoare de resurse de calcul. Cu cât trebuie modelată o gamă mai largă de scări ale lungimilor și timpului, cu atât efortul de calcul crește. Costul calculului este proporțional cu puterea a treia a numărului Reynolds (Re),[38] ceea ce duce la posibilitatea abordării doar a curgerilor cu Re mic, pentru curgeri simple, în domenii cu geometrii simple. Dificultăți suplimentare apar datorită faptului că termenii de convecție și presiune sunt neliniari. Toate aceste ecuații neliniare trebuie soluționate numeric, cu condițiile inițiale și la limită impuse.
Modele semiempirice[modificare | modificare sursă]
Aceste modele implică folosirea unor ecuații algebrice pentru tensiunile Reynolds (v. mai jos) ecuații care presupun și determinarea viscozității turbulente, ca sumă între viscozitatea dinamică și un termen cu semnificația de viscozitate aparentă. Acuratețea modelării a producerii turbulenței (de obicei prin mărimea energia cinetică turbulentă – k) și a disipației turbulenței (de obicei prin mărimea disipația turbulentă – ε) depinde de gradul de complexitate al modelului. Pentru modelarea acestor mărimi se folosesc ecuații algebrice sau ecuații diferențiale semiempirice, adică în acord cu teoria propusă și cu constantele stabilite pe cale experimentală. Convențional, numărul de ecuații al modelului este cel al ecuațiilor diferențiale. Ca urmare, există modele cu zero, una și două ecuații.[39]
- Modele cu „zero” ecuații
Presupunerea care se face în aceste modele este că producția și disipația turbulenței sunt relativ egale, ca urmare nu este necesară modelarea convecției turbulenței. Această presupunere se îndepărtează mult de fenomenul cunoscut, însă modelul poate fi implementat ușor și în unele domenii rezultatele sunt satisfăcătoare. Exemple de astfel de modele sunt modelul regiunii interioare/exterioare, modelul Cobeci/Smith sau modelul Baldwin–Lomax. În aceste modele atât viscozitatea turbulentă, cât și scările de viteze și timp sunt modelate prin ecuații algebrice.[40]
- Modele cu o ecuație
Aceste modele folosesc o singură ecuație diferențială. Exemple de astfel de modele sunt Baldwin–Barth și Spalart–Allmaras.[41] În modelul Baldwin–Barth atât producția, cât și disipația sunt modelate într-o singură ecuație diferențială, în timp ce pentru viscozitatea turbulentă se folosește o ecuație algebrică.[42] Aceste modele sunt satisfăcătoare la curgerea peste profile aerodinamice, unde disipația turbulentă prezintă mai puțin interes.
- Modele cu două ecuații
În aceste modele atât producția, cât și disipația turbulenței sunt modelate cu câte o ecuație diferențială, ceea ce face ca modelul să fie adecvat pentru curgeri în domenii cu geometrii complexe. Exemple de astfel de modele sunt modelul k-ε[43] și modelul k-ω.[44][45]
Medierea Reynolds[modificare | modificare sursă]

În medierea Reynolds luarea în considerare a efectelor turbulențelor de scări mici se face prin medierea în timp a ecuațiilor exacte,[46] rezultând ecuații care pot fi calculate cu un efort numeric rezonabil.
Componentele vitezei la momentul într-un punct sunt considerate ca suma dintre componenta corespunzătoare a vitezei medii (mediată în timp) și componenta fluctuantă:[47]
Înlocuind această expresie în ecuația de conservare a impulsului se obțin ecuațiile Navier-Stokes mediate Reynolds (engleză Reynolds-averaged Navier–Stokes equations – RANS), care pentru curgerea staționară a unui fluid newtonian incompresibil au forma:
În aceste ecuații termenii adiționali care apar sunt cei de forma , se numesc tensiuni Reynolds și au semnificația de tensiuni aparente.[48]
Există două abordări în modelul RANS:
- Ipoteza Boussinesq
Această metodă presupune rezolvarea unei ecuații algebrice pentru tensiunile Reynolds, care include determinarea viscozității turbulente. Depinde de complexitatea modelului modul în care sunt calculate energia cinetică turbulentă și disipația turbulentă. Asta se poate face cu diferite modele de turbulență semiempirice, prezentate anterior.
- Modelul tensiunilor Reynolds (engleză Reynolds stress model – RSM)
Această metodă rezolvă un set suplimentar de ecuații de transport, pentru tensiunile Reynolds. Rezolvarea acestor ecuații de transport consumă resurse de calcul suplimentare.
Simularea vârtejurilor mari[modificare | modificare sursă]

Simularea vârtejurilor mari (engleză large eddy simulation – LES) este o tehnică în care turbulența este modelată în două moduri. Vârtejurile mai mari decât scara rețelei de discretizare, separate printr-o tehnică de filtrare, sunt modelate ca atare, în timp ce cele mai mici sunt modelate folosind modele de turbulență semiempirice. Asta permite calculul vârtejurilor mari, cu efect important, fără a consuma resurse exagerate pentru calculul turbulențelor la scară mică. Resursele de calcul necesare sunt mai mari ca cele pentru metoda RANS, dar mult mai mici decât cele pentru metoda DNS.[49]
Simularea vârtejurilor detașate[modificare | modificare sursă]
Simularea vârtejurilor detașate (engleză detached eddy simulation – DES) este o metodă hibridă între RANS și LES propusă în 1997 și aplicată în 1999. Zonele de lângă pereți, unde scara turbulenței este mai mică, sunt modelate cu RANS, iar zonele cu scări de turbulență mai mari sunt modelate prin LES. Discretizarea domeniului este mai complicată decât cea doar pentru RANS sau LES, însă nu trebuie să fie așa de fină ca la LES, ceea ce reduce efortul de calcul. Trecerea de la un model la altul nu este pe zone, ceea ce asigură o trecere lină de la valorile calculate cu RANS la cele calculate prin LES.[50]
Simularea coerentă a vorticității[modificare | modificare sursă]
Simularea coerentă a vorticității (engleză coherent vortex simulation – CVS) abordează modelarea mișcării turbulente prin descompunerea curgerii cu vârtejuri într-o parte coerentă, având vorticitate organizată, și o parte incoerentă, cu turbulență stocastică.[51] Este o metodă care face apel la filtrare, fiind asemănătoare cu LES. Diferența față de LES este că filtrarea se face cu funcția wavelet (funcția wavelet are forma de val mic). Farge și Schneider au testat metoda CVS și au arătat că porțiunea din spectrul energetic al părții coerente este semnificativă.[52]
Metode de tip PDF[modificare | modificare sursă]
Metodele de tip funcția densitate a probabilității (engleză probability density function – PDF) au fost introduse în studiul turbulenței de Lundgren, în 1969.[53] Viteza este modelată cu o funcție PDF, care dă probabilitatea vitezei în punctul ca fiind între și . Această abordare este similară cu cea din teoria cinetico-moleculară a gazelor. Metodele PDF se pot aplica în diferite modele ale turbulenței, obținându-se diferite ecuații de transport. De exemplu, în metoda LES, metoda PDF devine metoda PDF filtrată,[54] Metodele PDF se pot folosi și în modelarea reacțiilor chimice,[55][56] unde sunt foarte utile deoarece problema termenilor sursă chimici este închisă, deci nu necesită un model.
MFN în transmiterea căldurii[modificare | modificare sursă]
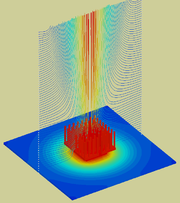
Transmiterea căldurii este un domeniu care face apel la tehnicile folosite în MFN. Căldura se poate transmite prin conducție, convecție și radiație.

Transmiterea prin conducție are loc în special în corpuri solide, conform ecuației Fourier, a cărei formă diferențială este:[57][58]
unde este fluxul termic, este conductivitatea termică, iar este gradientul temperaturii. Conductivitatea termică este considerată adesea constantă, dar în realitate ea depinde de temperatură. În simulări ea poate fi calculată cu o relație algebrică. În caz că materialul nu este izotrop, ea este un tensor.
În ecuația Fourier apare operatorul nabla, ca urmare dezvoltările pentru MFN se pot aplica cu modificări minime la modelarea conducției.[57]
În transmiterea prin convecție rolul conducției este minim, însă rolul turbulenței este foarte important. Metodele MFN pentru modelarea curgerilor turbulente sunt absolut necesare la modelarea schimbului de căldură prin convecție.
Transmiterea căldurii prin radiație ridică dificultăți, deoarece ecuațiile transmiterii căldurii prin radiație sunt ecuații integrale, de forma:
unde este intensitatea radiației, este vectorul de poziție, este vectorul de direcție, este lungimea drumului parcurs, este direcția disipației, este coeficientul de absorbție, este indicele de refracție, este coeficientul de disipație, este constanta Stefan–Bolzmann, este temperatura locală, este funcția de fază, iar este unghiul solid.[59][60]
Ecuația integrală nu poate fi adusă la forma ecuațiilor diferențiale, ca urmare nu poate fi inclusă direct în sistemul de ecuații diferențiale ale MFN, fiind nevoie de modele de radiație. Există diferite modele de radiație, cum ar fi de exemplu modelul P-1[61], modelul Rosseland[62], modelul radiației prin transfer discretizat[63] (engleză discrete transfer radiation model[64] – DTRM), modelul radiației prin ordonate discretizate[63] (engleză discrete ordinates[65] – DO), modelul radiației suprafață către suprafață (engleză surface to surface radiation model – S2S)[66], respectiv modelul sumei ponderate a gazelor gri (engleză the weighted-sum-of-gray-gases model – WSGGM).[67]
MFN în transportul speciilor chimice[modificare | modificare sursă]
Transportul speciilor chimice este un domeniu necesar pentru transmiterea căldurii. Transmiterea căldurii prin mecanismele cunoscute este relativ lentă, adesea mult prea lentă pentru a fi utilă pentru mașinile termice. Aproape întotdeauna introducerea de căldură într-un ciclu termodinamic se face printr-o reacție chimică exotermă. Ca urmare, s-au dezvoltat modele pentru:
- viteza de reacție, transportul speciilor chimice, reacții de suprafață (depuneri, reacții la suprafața particulelor solide),[68]
- reacții de ardere cinetice (engleză premixed[69]) și difuzive (engleză non-premixed[70]).
- aprinderea în motoarele cu ardere internă,[71]
- formarea poluanților în urma arderii.[72]
Condiții la limită[modificare | modificare sursă]
Condițiile la limită sunt restricții impuse pe frontierele domeniului de analiză.[73] Aceste restricții pot fi de două tipuri:
- condiții la limită de tip Dirichlet (numite și esențiale[74][75]), în care se impun valorile variabilei dependente pe frontiera specificată,[73]
- condiții la limită de tip Neumann (numite și naturale[74][75]), în care se impune gradientul variabilei dependente în direcție normală pe frontiera specificată.[73]
Dacă pe frontiera specificată se impun atât condiții Dirichlet, cât și Neumann, se vorbește de condiții de tip Cauchy.[73] Dacă pe frontiera specificată se impun combinații liniare de condiții Dirichlet și Neumann se vorbește despre condiții de tip Robin.[74] Dacă pe diferite părți ale frontierei domeniului se impun condiții la limită de tipuri diferite se spune că este vorba despre condiții mixte.[74]
Discretizarea ecuațiilor[modificare | modificare sursă]
Ținând cont că un computer poate executa doar operații matematice simple, ecuațiile diferențiale prezentate anterior trebuie aduse la o formă algebrică, adecvată programării. Această transformare este cunoscută drept discretizarea ecuațiilor.[76]
Stabilitatea calculului numeric a ecuațiilor discretizate nu poate fi prevăzută analitic, ea se demonstrează în practică. Această stabilitate este pusă la încercare în special în zona discontinuităților. Atât ecuațiile lui Euler, cât și ecuațiile Navier–Stokes admit discontinuități, astfel că uneori stabilitatea este o problemă.
În continuare sunt prezentate diferite metode de discretizare a ecuațiilor.
Metoda diferențelor finite[modificare | modificare sursă]

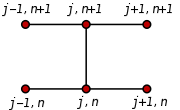
În metoda diferențelor finite (MDF)[76] (engleză finite difference method – FDM), infinitezimalele din derivate sunt transformate în diferențe.[77] Acest procedeu este unul natural, deoarece derivata unei funcții este, prin definiție:
astfel că pentru un mic expresia:
este o aproximare acceptabilă. Astfel este posibilă obținerea soluției fără a calcula derivatele.
În discretizare ecuațiile sunt dezvoltate în serie Taylor, care se trunchiază convenabil.[77] Diferențele se scriu pentru puncte amplasate pe o grilă (rețele ortogonale), existând diferite scheme, una dintre cele mai cunoscute fiind schema Crank–Nicolson.[76]
Istoric, discretizarea prin metoda diferențelor finite a fost prima. Ea este relativ simplă, ușor de programat și nu consumă resurse de calcul mari. Inițial, metoda s-a folosit pe domenii discretizate cu grile ortogonale, care făceau dificilă tratarea geometriilor curbilinii. Dezvoltarea metodei pentru rețele neortogonale a complicat mult situația, anulând practic avantajele inițiale.
Metoda elementelor finite[modificare | modificare sursă]


Metoda elementelor finite(d) (MEF) (în engleză finite element method – FEM), cunoscută în literatura de specialitate din România și ca metoda elementului finit[76] este răspândită în special în analiza structurală a solidelor, dar este aplicabilă și fluidelor. Ideea metodei elementelor finite este de a aproxima soluția ecuațiilor diferențiale cu combinații liniare ale funcțiilor diferențiale liniarizate pe domenii mici (finite) și funcții de ponderare (funcții de interpolare). Obținerea formulării slabe, necesare calculului numeric se poate face prin metoda Galerkin sau prin formularea variațională.[78][79][80][81] Ecuațiile diferențiale care descriu fenomenele (de exemplu ecuațiile Navier–Stokes) se reformulează într-o formă conservativă și apoi se discretizează această nouă formă. Este dificil de reformulat aceste ecuații astfel încât să se obțină o formă conservativă. Dacă însă se reușește (de exemplu pentru fenomenul modelat), calculul numeric este mult mai stabil decât în cazul metodei volumelor finite.[82]
Domeniul de analiză este împărțit în mici subdomenii, elemente finite. În funcție de numărul de dimensiuni ale domeniului pot exista elemente finite unidimensionale, bidimensionale sau tridimensionale. Pentru un element, valorile funcțiilor se calculează într-un număr discret de puncte, numite noduri. De obicei acestea sunt plasate la extremitățile elementelor, dar nu este obligatoriu. Mulțimea nodurilor dintr-un element determină dimensiunea unei matrice locale a elementului. În marea majoritate a cazurilor un nod, de exemplu dintr-un colț al unui element, face parte și din colțul altui element, astfel că este nevoie de asamblarea matricelor locale într-o matrice globală a domeniului. Asamblarea se face cu ajutorul unei matrice de conexiuni, rezultând o matrice a sistemului de rezolvat foarte mare, de ordinul numărului de noduri din domeniu, înmulțit cu numărul de variabile necunoscute.[83]
Problemele teoretice care tratează existența, unicitatea și acuratețea soluțiilor obținute prin aproximarea prin Metoda Elementelor Finite sunt prezentate pe larg în lucrări matematice de specialitate.[84]
Metoda volumelor finite[modificare | modificare sursă]
În metoda volumelor finite (MVF) (engleză finite volume method – FVM) ecuațiile care descriu fenomenele sunt rezolvate pentru mici volume de control,[85] volume finite (celule), în care este impusă conservarea proprietăților la trecerea prin suprafața volumului de control astfel, cantitatea de proprietate care iese dintr-un volum de control intră (este transportată) în volumul de control adiacent. Ca urmare, nu există generare sau eliminare arbitrară a proprietăților. Metoda este consumatoare de resurse, deoarece mărimea transportată printr-o suprafață trebuie să fie egală în ambele volume adiacente, doar cu semn schimbat.[86] Ecuațiile pot fi discretizate atât prin MDF,[87] cât și prin MEF.[88]
Metoda elementelor de frontieră[modificare | modificare sursă]
În metoda elementelor de frontieră (MEFr) (engleză boundary element method – BEM), ecuațiile diferențiale sunt rezolvate doar pe frontieră, care este singura discretizată, rezultând un număr de noduri mai mic, corespunzător unei dimensiuni în minus. Ecuațiile trebuie să fie liniare sau liniarizate. În interiorul domeniului soluția este cea dată de suprafața generată de soluția teoretică, care pe frontieră corespunde soluției calculate.[89]
Rețele de discretizare[modificare | modificare sursă]


Odată stabilită forma domeniului de analiză, acesta trebuie desenat și ulterior discretizat. Desenarea se poate face practic cu orice pachet CAD/CAE. Discretizarea unui domeniu de analiză bidimensional se face de obicei cu triunghiuri sau patrulatere,[90] iar discretizarea unui domeniu tridimensional cu tetraedre, hexaedre, prisme triunghiulare (sau pene), piramide patrulatere,[91] sau, mai nou, cu poliedre neregulate. Discretizarea cu poliedre neregulate duce la scăderea de câteva ori a numărului de celule necesare pentru obținerea aceleiași precizii a rezultatului,[92] însă numărul de noduri (care determină mărimea sistemului de ecuații de rezolvat, respectiv efortul de calcul) nu scade în aceeași măsură. Se pot folosi simultan mai multe tipuri de elemente de discretizare, caz în care rețeaua este hibridă.[93]
În timpul calculului rutina de rezolvare a sistemului de ecuații generat trebuie să știe care sunt celulele adiacente fiecărei celule, respectiv care dintre noduri, laturi și fețe sunt comune la două sau la mai multe celule. Aceste informații sunt stocate în matricea de conexiuni. Dacă nodurile rețelei sunt dispuse regulat, informațiile din matricea de conexiuni pot fi generate în timp real printr-un algoritm, iar existența matricei de conexiuni nu este necesară. Rețeaua de discretizare este în acest caz structurată.[93][94][95] În general rețelele structurate sunt rețele simple. Pentru geometrii sau moduri de discretizare complexe, când nu există un algoritm (ex.: nodurile rețelei au fost distribuite neregulat), sau algoritmul nu este disponibil (ex. rețeaua a fost generată cu altă aplicație, iar algoritmul acesteia nu s-a transmis rutinei de rezolvare) matricea de conexiuni este necesară, iar despre rețea se spune că este nestructurată.[93][96][97] O rețea de discretizare nestructurată poate fi însă adaptată în funcție de rezultatele intermediare ale calculului, ea putând fi rafinată (îndesită) sau rărită în unele zone, după cum se consideră că este necesar.[93][98][99]
Rezolvarea sistemului de ecuații global[modificare | modificare sursă]

Orice metodă de discretizare a ecuațiilor și a domeniului de analiză conduce în cazul problemelor staționare (independente de timp) la rezolvarea unui sistem de ecuații liniare de forma , iar în cazul problemelor nestaționare la rezolvarea unui sistem de ecuații diferențiale, care și el trebuie liniarizat.[100][101] Matricea este o matrice rară.[102] Printr-o renumerotare a nodurilor matricea A devine o matrice bandă,[102] mai ușor de tratat. Prin renumerotarea optimă a nodurilor lățimea benzii matricei poate fi minimizată.[102] Prin înmulțirea la stânga a matricei sistemului de ecuații cu transpusa sa produsul matricial devine o matrice bandă simetrică, cu diagonala principală dominantă, ceea ce asigură stabilitatea și convergența algoritmilor de rezolvare.[103]
Metode de rezolvare a sistemului[modificare | modificare sursă]
Soluționarea sistemului global de ecuații poate fi făcută prin metode directe și metode iterative. Metodele directe rezolvă sistemul global de ecuații printr-o singură trecere. Avantajele lor sunt că rezolvarea se face într-un interval de timp cunoscut, iar la algoritmi buni și o programare îngrijită se pot rezolva sisteme cu câteva mii de ecuații cu o eroare de calcul rezonabilă.[103] Totuși, eroarea de calcul, determinată în special de erorile de trunchiere, nu poate fi controlată în timpul rezolvării, ci doar în testele preliminare. Metodele directe sunt adecvate pentru rezolvări de sisteme liniare cu o singură variabilă. Dacă sistemele au mai multe variabile, a căror comportare este neliniară, rezolvarea lor se poate face numai prin metode iterative.[104]
Metodele iterative rezolvă sistemul global de ecuații prin iterații succesive. Fiecare iterație calculează o nouă soluție, pe baza soluției precedente. Pentru pornirea calculului este nevoie de o soluție inițială, dată de utilizator. Această soluție poate fi destul de departe de soluția reală, însă cu cât soluția inițială este mai bună, cu atât este mai probabil ca stabilitatea calculului să fie mai bună și efortul de calcul mai mic. Pentru îmbunătățirea stabilității, în special la rezolvarea ecuațiilor neliniare, se folosește subrelaxarea, adică corecțiile se iau mai mici decât cele rezultate din calcul.[105] După fiecare iterație sunt verificate reziduurile. Reziduul este dat de expresia , unde este soluția după iterația n. Cu cât reziduul este mai mic, cu atât soluția calculată satisface mai bine sistemul de ecuații. Dacă în timpul calculului reziduul scade, soluția calculată converge spre soluția reală. Când reziduul este suficient de mic, calculul poate fi considerat terminat.[104]
Calcul paralel[modificare | modificare sursă]
MFN, având nevoie de cât mai multă putere de calcul, beneficiază din plin de soluțiile hardware ale calculatoarelor, cum ar fi prelucrarea vectorială (în paralel) sau tehnica pipelined.[106]
O altă posibilitate este rezolvarea în rețea, folosind mai multe unități de calcul în paralel. În acest scop, matricea globală este împărțită conform resurselor disponibile. Există rețele cu memorie distribuită (de exemplu calculatoare individuale conectate în rețea) și stații cu mai multe procesoare, cu memorie partajată. Fiecare procesor prelucrează partea sa de matrice și apoi, după un anumit număr de iterații, schimbă între ele rezultatele. Schimbul de informații în rețele de calculatoare individuale este relativ lent, astfel că algoritmii trebuie să minimizeze aceste schimburi.[106]
Distribuirea sarcinilor se face în funcție de posibilități. De exemplu în sistemul de operare Windows XP un proces nu poate accesa o memorie mai mare de 2G, ca urmare o memorie de 4G nu poate fi exploatată decât „în rețea”, lansând două procese, chiar dacă există o singură unitate de calcul (engleză core), prin partajarea timpului. Evident, se pot folosi mai multe unități de calcul în paralel, eventual și cu partajarea timpului, de exemplu 16 procese lansate pe un procesor quad. Pentru aplicațiile comerciale este însă nevoie de câte o licență pentru fiecare proces.
Etapele unei modelări practice[modificare | modificare sursă]
În cursul unei aplicații practice privind modelarea numerică a curgerii fluidelor sunt parcurse patru etape. Prima etapă este cea a analizei problemei. În această etapă se stabilesc obiectivele modelării, mărimile de interes, adică mărimile necunoscute care vor fi calculate și care sunt semnificative pentru problema studiată, se definește domeniul de analiză, se aleg modelele matematice ce vor fi folosite și se stabilesc condițiile la limită necesare.[107][108] Această etapă solicită din plin competența în domeniu a persoanei care concepe modelarea.
A doua etapă este cea de discretizare a domeniului, etapă în care se stabilește forma geometrică detaliată a domeniului care asigură atât încadrarea spațială a problemei studiate, cât și posibilitatea introducerii corecte a condițiilor la limită. În această etapă se face desenarea acestui domeniu și este discretizat, rezultatul acestei etape fiind rețeaua de discretizare.[107][108] Această etapă este considerată o „preprocesare”, poate fi parcursă independent de cea care urmează și adesea folosește resurse hardware și software diferite de cele folosite de aplicația MFN propriu-zisă. Din punct de vedere al manoperei, această etapă este cea mai solicitantă.
A treia etapă este efectuarea propriu-zisă a modelării cu ajutorul unor resurse hardware și software adecvate aplicației MFN propriu-zise. Este importată rețeaua de discretizare generată în etapa precedentă. Se alege setul de ecuații care modelează fenomenele caracteristice problemei studiate, eventual acest set este completat cu adaosuri programate de persoana care utilizează aplicația. Sunt definite proprietățile fizice ale substanțelor și condițiile la limită. Apoi se trece la soluționarea numerică a problemei.[107][108] Această etapă consumă cele mai mari resurse de calcul.
Rezultatul obținut în etapa de calcul este obținut în formă numerică, formă greu de interpretat direct de om, motiv pentru care în ultima etapă are loc postprocesarea grafică a rezultatelor, în care sunt calculate mărimi derivate din cele obținute în etapa de soluționare numerică și sunt trasate o serie de reprezentări grafice ale rezultatelor.[107][108]
Pentru rezolvarea problemelor netriviale, în afară de resursele hardware și software costisitoare[109] este necesară și o experiență considerabilă, resurse care nu sunt la îndemâna unui agent economic obișnuit.
Exemple de modelări[modificare | modificare sursă]
- Modelări ale curgerilor exterioare
Curgerile exterioare (în jurul corpurilor) diferă de curgerile interioare (în canale) prin faptul că spațiul, teoretic nemărginit, trebuie redus la un domeniu, de obicei cu dimensiunea liniară de câteva ori mai mare decât a corpului. Este nevoie de rețele de doscretizare mai dese în apropierea corpului, rețele care pot deveni tot mai rare cu depărtarea de corp. Dacă curgerea este supersonică (produce unde de șoc), în dreptul saltului de presiune rețeaua trebuie să fie din nou deasă. Cum poziția undei de șoc nu este cunoscută dinainte, tehnicile de rafinare a rețelei de discretizare pe baza rezultatelor intermediare devin strict necesare. Exemple de astfel de aplicații sunt determinarea presiunilor și a liniilor de curgere în aviație, marină și industria automobilelor.
- Curgeri exterioare în jurul unor corpuri
-
Câmp de presiuni în jurul unei navete spațiale.
-
Coeficientul de presiune în jurul unui automobil.
-
Câmp de viteze și presiuni în jurul unei mașini de Formula 1.
-
Câmp de presiuni la prova unei nave.
-
Viteze ale vântului în jurul unei clădiri.
- Modelarea unui domeniu periodic

Un exemplu mai aparte al MFN este posibilitatea exploatării simetriilor și periodicităților domeniului de analiză. Asta se aplică în special în domeniul turbomașinilor, unde este suficientă discretizarea curgerii într-un canal interpaletar, curgerea prin celelalte canale comportându-se practic identic. Curgerea în rotorul unei turbine nu este una plană sau axial-simetrică, ca urmare domeniul de curgere nu poate fi discretizat 2D sau 2½D, fiind nevoie de o discretizare 3D. Apa care curge printr-o turbină hidraulică poate fi considerată incompresibilă, și, deoarece dimensiunile rotorului sunt destul de mari ca influența frecărilor să fie neglijabilă, fluidul poate fi considerat neviscos, astfel că modelarea vitezelor se poate face cu ecuațiile Euler, mai simple ca cele Navier–Stokes. Figura alăturată prezintă unul din rezultatele obținute, și anume, distribuția coeficientului de presiune pe 11 din cele 13 palete ale rotorului (două palete au fost omise la prelucrarea grafică a rezultatelor pentru claritatea imaginii). Odată obținut câmpul de presiuni, se pot face considerații privind regimul cavitațional sau se poate continua simularea introducând un model al cavitației.[110]
- Modelarea unor curgeri cu reacții chimice și transfer termic
Exemplul tipic pentru această combinație este modelarea focarelor cazanelor, în special în contextul reducerii emisiilor poluante. Este nevoie de modele care să trateze curgerea turbulentă din focar, variația densității gazelor cu temperatura, antrenarea fazelor disperse (praf de combustibil) de către mediul fluid, reacțiile chimice exoterme dintre combustibil și oxidant, schimbul de căldură prin radiație, și mecanisme Zeldovici și Fenimore de formare a NO.[111]
- Aspecte ale modelării unui focar al unui cazan de abur
-
Câmpul de viteze.
-
Traiectoriile particulelor de combustibil.
-
Temperaturi.
-
Concentrații ale CO2.
-
Concentrații ale NO.
MFN în România[modificare | modificare sursă]
Preocupări privind MFN în România au apărut prima dată la Universitatea Politehnica din București, Facultatea de Aeronave.[112]
În anii 1990 în cadrul Universității Politehnica din Timișoara a fost scrisă aplicația ROFEM, destinată să ruleze pe computere personale, având la bază ecuația Laplace, aplicație cu care s-au modelat în 2D și 2½D (domenii axial-simetrice) funcția de curent[113] și potențialul vitezei[114] în rețele de profile,[115] contracția jetului liber[116][117] și fenomene termice[103] pe rețele de discretizare cu până la 16 000 de noduri.[118]
Tot în cadrul Universității Politehnica din Timișoara a luat ființă Centrul Național pentru Ingineria Sistemelor cu Fluide Complexe (CNISFC), care dispune de un laborator de calcul paralel cu zece calculatoare legate în rețea, accesibile studenților[119] și stații de calcul paralel destinate cercetării. Aplicația de bază pentru MFN a centrului este ANSYS-FLUENT, iar principalul domeniu de cercetare este cavitația în turbinele hidraulice.[120]
Aplicația ANSYS-FLUENT este folosită și la alte universități din România, ca Universitatea Politehnica din București, Universitatea Tehnică de Construcții din București, Universitatea Tehnică Gheorghe Asachi din Iași, Universitatea Tehnică Cluj-Napoca, Universitatea „Dunărea de Jos”.[121]
Vezi și[modificare | modificare sursă]
Note[modificare | modificare sursă]
- ^ Resiga, 2003
- ^ „Programa analitică pentru disciplina Mecanica Fluidelor și Mașini Hidraulice, Facultatea de Electrotehnică, anul II”. Arhivat din original la . Accesat în .
- ^ Autodesk a realizat un acord de preluare a Blue Ridge Numerics Inc., maxcad.ro, 23 februarie 2011, accesat 2011-03-14
- ^ Broboană, Muntean Vol II p 26
- ^ en Dmitri Kuzmin, Introduction to Computational Fluid Dynamics, uni-dortmund.de, accesat 2011-04-3
- ^ a b Landau, pp. 62-65
- ^ Landau, pp. 11-14
- ^ Landau, pp. 26-31
- ^ en Milne-Thomson, L.M. (). Theoretical Aerodynamics. Dover Publications. ISBN 048661980X.
- ^ en Hess, J.L. (). „Calculation of Potential Flow About Arbitrary Bodies”. Progress in Aeronautics Sciences. 8: 1–138. doi:10.1016/0376-0421(67)90003-6.
- ^ Resiga, 2003, pp.64-70
- ^ en „NASCART”. Daniel Guggenheim School of Aerospace Engineering. Arhivat din original la . Accesat în .
- ^ Resiga, 2003, p. 12
- ^ en Ian N. Sneddon, Elements of Partial Differential Equations, Ed. McGraw Hill, 1957
- ^ a b c d e Chung, pp. 389-390
- ^ Chung, p. 63
- ^ Chung, p. 67
- ^ Chung, p. 77
- ^ Landau, pp. 9-11
- ^ Hoffmann, pp. 12-14
- ^ Resiga, 1999, pp. 23-24
- ^ Oprișa-Stănescu, p. 30
- ^ Hoffmann, pp. 14-28
- ^ Resiga, 2003, pp. 24-25
- ^ Chung, p. 92
- ^ Chung, p. 93
- ^ Hoffmann, pp. 29-37
- ^ Resiga, 1999, pp. 26-27
- ^ Patankar, pp. 113-114
- ^ Patankar, pp. 126-129
- ^ Patankar, pp. 131-134
- ^ Olsen, pp. 28-35
- ^ en Variants of SIMPLE: SIMPLER & SIMPLEC Arhivat în , la Wayback Machine., purdue.edu, accesat 2011-03-26
- ^ J. H. Ferziger, M. Peric, Computational Methods for Fluid Dynamics, Springer, 3rd Ed., 2001
- ^ I. E. Barton Comparison of SIMPLE- and PISO-type algorithms for transient flows International Journal of Numerical Methods in Fluids, vol. 26, Issue 4, pp.459-483, 28 February 1998, DOI: 10.1002/(SICI)1097-0363(19980228)26:4<459::AID-FLD645>3.0.CO;2-U
- ^ Oprișa-Stănescu, p. 43-45
- ^ Sterian Dănăilă ș.a., Metode și soluții moderne în analiza instabilității mișcării laminare și apariției tranziției Arhivat în , la Wayback Machine., contract CNCIS-IDEI nr. 109/2007-10-01, accesat 2011-03-20
- ^ en Pope, S. B. (). Turbulent Flows. Cambridge University Press. ISBN 978-0521598866.
- ^ Chung, p. 194
- ^ Chung, pp. 199-203
- ^ en Philippe R. Spalart, Steve R. Allmaras, A One-Equation Turbulence Model for Aerodynamic Flows. Technical Report AIAA-92-0439, American Institute of Aeronautics and Astronautics, 1992
- ^ Chung, pp. 203-205
- ^ en Brian E. Launder, Dudley B. Spalding, (1974), "The numerical computation of turbulent flows", Computer Methods in Applied Mechanics and Engineering, 3(2): 269-289
- ^ en Wolfgang Rodi, Turbulence models and their application in hydraulics - a state of the art review, International Association for Hydraulic Research, Delft, 3rd edition 1993, Balkema
- ^ Chung, pp. 205-208
- ^ Patankar, pp. 14-15
- ^ Landau, p. 146
- ^ Chung, pp. 195-198
- ^ Oprișa-Stănescu, p. 54
- ^ en Philippe R. Spalart, Detached-Eddy Simulation Arhivat în , la Wayback Machine., Annual Review of Fluid Mechanics, Vol. 41: 181-202 (2009), DOI: 10.1146/annurev.fluid.010908.165130, accesat 2011-03-21
- ^ en Farge, Marie; Schneider, Kai. „Coherent Vortex Simulation (CVS), A Semi-Deterministic Turbulence Model Using Wavelets”. Flow, Turbulence and Combustion. 66 (4): 393–426. doi:10.1023/A:1013512726409.
- ^ en Goldstein, Daniel; Vasilyev, Oleg (). „Stochastic coherent adaptive large eddy simulation method”. Physics of Fluids A. 24: 2497. doi:10.1063/1.1736671.
- ^ en Lundgren, T.S. (). „Model equation for nonhomogeneous turbulence”. Physics of Fluids A. 12 (3): 485–497. doi:10.1063/1.1692511.
- ^ en Colucci, P. J.; Jaberi, F. A; Givi, P.; Pope, S. B. (). „Filtered density function for large eddy simulation of turbulent reacting flows”. Physics of Fluids A. 10 (2): 499–515. doi:10.1063/1.869537.
- ^ en Fox, Rodney (). Computational models for turbulent reacting flows. Cambridge University Press. ISBN 978-0-521-65049-6.
- ^ en Pope, S. B. (). „PDF methods for turbulent reactive flows”. Progress in Energy and Combustion Science. 11: 119–192.
- ^ a b Landau, pp. 227-240
- ^ Patankar, pp. 59-60
- ^ en ANSYS, Radiative Transfer Equation Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ Oprișa-Stănescu, p. 57
- ^ en ANSYS, P-1 Radiation Model Theory Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Rosseland Radiation Model Theory Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ a b Oprișa-Stănescu, pp. 58-65
- ^ en ANSYS, Discrete Transfer Radiation Model (DTRM) Theory Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Discrete Ordinates (DO) Radiation Model Theory Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Surface-to-Surface (S2S) Radiation Model Theory Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, The Weighted-Sum-of-Gray-Gases Model Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Modeling Species Transport and Finite-Rate Chemistry Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Modeling Premixed Combustion Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Modeling Non-Premixed Combustion Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Modeling Engine Ignition Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ en ANSYS, Modeling Pollutant Formation Arhivat în , la Wayback Machine., my.fit.edu, accesat 2011-03-22
- ^ a b c d Chung, pp. 13-14
- ^ a b c d Heinrich, pp. 23-24
- ^ a b Resiga, 2003, p. 30
- ^ a b c d Dorin Lelea, Metode numerice avansate în transferul de căldură, Timișoara: Ed. „Politehnica”, 2007, ISBN 978-973-625-508-3, pp. 17-22
- ^ a b Chumg, pp. 45-46
- ^ Chung, p. 245
- ^ Heinrich, pp. 37-39
- ^ Resiga, 2003, pp. 85-99
- ^ Mihai Gafițanu, Victor-Florin Poterașu, Nicolae Mihalache, Elemente finite și de frontieră cu aplicații la calculul organelor de mașini, București: Ed. Tehnică, 1987
- ^ en Surana, K.A.; Allu, S.; Tenpas, P.W.; Reddy, J.N. (). „k-version of finite element method in gas dynamics: higher-order global differentiability numerical solutions”. International Journal for Numerical Methods in Engineering. 69 (6): 1109–1157. doi:10.1002/nme.1801.
- ^ Chung, p. 247
- ^ Titus Petrila, Călin Ioan Gheorghiu, Metode element finit și aplicații, București, Ed. Academiei, 1987
- ^ Patankar, p. 30
- ^ Chung, p. 219
- ^ Chung, pp. 218-239
- ^ Chung, pp. 491-518
- ^ Chung, p.522
- ^ Olsen, p. 8
- ^ Heinrich, pp. 484-495
- ^ en Martin Spiegel ș.a., Tetrahedral vs. polyhedral mesh size evaluation on flow velocity and wall shear stress for cerebral hemodynamic simulation, informatik.uni-erlangen.de, accesat 2011-03-23
- ^ a b c d Oprișa-Stănescu, pp. 13-16
- ^ Olsen, pp. 9-11
- ^ Heinrich, p. 474
- ^ Olsen, p. 11
- ^ Heinrich, p. 484
- ^ Heinrich, pp. 490-495
- ^ Heinrich, pp. 508-528
- ^ en Shan-Fu Shen, Wagdi G. Habashi, Local linearization of the finite element method and its applications to compressible flows, International Journal for Numerical Methods in Engineering, vol. 10, iss. 3, pp. 565–577, 1976
- ^ Elie Carafoli, Virgiliu N. Constantinescu, Dinamica fluidelor compresibile, București: Editura Academiei, 1986, p. 785
- ^ a b c Heinrich, pp. 495-507
- ^ a b c Paul-Dan Oprișa-Stănescu, Studiul și modelarea fenomenelor de ardere cu aplicație la arderea cărbunelui pulverizat în focarele cazanelor industriale, Teză de doctorat, Universitatea „Politehnica” din Timișoara, 1996
- ^ a b Oprișa-Stănescu, p. 26
- ^ Patankar, p. 67
- ^ a b Chung, pp. 656-665
- ^ a b c d Prisecaru, pp. 6-11
- ^ a b c d Oprișa-Stănescu, p. 8
- ^ en CFD Tutorial Many examples and images, with references to robotic fish], societyofrobots.com, accesat 2011-03-25
- ^ Sebastian Muntean, Analiza numerică a curgerii în turbinele hidraulice Francis, Timișoara, Ed. Orizonturi Universitare, 2008, ISBN 978-973-638-355-7
- ^ Oprișa-Stănescu, pp. 103-129
- ^ Elie Carafoli, Virgiliu N. Constantinescu, Dinamica fluidelor incompresibile, București: Editura Academiei, 1981
- ^ 1999, pp. 138-141
- ^ 1999, pp. 142-143
- ^ Resiga, 1999, pp. 173-191
- ^ Resiga, 1999, pp. 191-210
- ^ Romeo Hidrodinamica jeturilor de mare viteză și aplicații, Teză de doctorat, Universitatea Politehnica din Timișoara, 1996
- ^ en Paul-Dan Oprișa-Stănescu, The "ROFEM" Finite Elements Analysis Package – Structure and Operating Mode, Bul. Șt. al Univ. Politehnica din Timișoara, tom 42(56), Fasc. 1, 1997, p.93-98, ISSN 1224-6077
- ^ Laboratorul de Simulare Numerică și Calcul Paralel al CNISFC Arhivat în , la Wayback Machine., Universitatea Politehnica Timișoara, accesat 2011-03-24
- ^ Sebastian Muntean, Metode numerice pentru determinarea câmpurilor tridimensionale în rotoarele turbinelor Francis, Teză de doctorat, Universitatea Politehnica din Timișoara, 2001
- ^ Vortex Hydrodynamics and Applications Arhivat în , la Wayback Machine., grant CNCSIS, Universitatea Politehnica Timișoara, accesat 2011-03-24
Bibliografie[modificare | modificare sursă]
- fr L.D. Landau, E.M. Lifchitz, Mécanique des fluids, Moscova: Ed. Mir, 1971, traducere după versiunea rusă din 1954.
- en Suhas Patankar, Numerical Heat Transfer and Fluid Flow, Taylor & Francis, 1980, ISBN 0891165223
- en Klaus A. Hoffmann, Steve T. Chang, Shannon Siddiqui, Michael Papadakis, Fundamental Equations of Fluid Mechanics, Wichita, KS: Engineering Education SystemTM, 1996, 67208-1078, ISBN 0-9623731-9-2
- en Juan C. Heinrich, Darell W. Pepper, Intermediate Finite Element Method, Castleton, NY: Hamilton Printing Co., 1999, ISBN 1-156032-309-4
- Romeo Resiga, Complemente de Mecanica Fluidelor și Tehnici de Soluționare Numerică, Timișoara: Ed. Orizonturi Universitare, 1999, ISBN 973-9400-60-4
- en Nils Reidar Bøe Olsen, CFD Algorithms for Hydraulic Engineering, e-book, 2000, ISBN 82-7598-044-5
- Tudor Prisecaru, Simularea numerică a proceselor de ardere a combustibililor gazoși și solizi pulverizați, București: Ed. BREN, 2001, ISBN 973-8143-76-4
- Paul-Dan Oprișa-Stănescu, Cristina Oprea, Simularea numerică a fenomenelor de ardere cu FLUENT, Timișoara: Ed. „Politehnica”, 2001, ISBN 973-8247-46-2
- en Harvard Lomax, Thomas H. Pulliam, David W. Zingg, Fundamentals of Computational Fluid Dynamics, Springer Verlag, 2001, ISBN 978-3540-41607-4
- en T.J. Chung, Computational Fluid Dynamics, Cambridge University Press, 2002, ISBN 0-521-59416-2
- Romeo Resiga, Mecanica Fluidelor Numerică[nefuncțională] (MFN), Timișoara: Ed. Orizonturi Universitare, 2003, ISBN 973-638-014-9
- Diana Broboană, Tiberiu Muntean, Corneliu Bălan, Mecanica fluidelor cu FLUENT, Editura Politehnica Press, 2006, ISBN 973-7838-06-8
- Diana Broboană, Tiberiu Muntean, Corneliu Bălan, Mecanica fluidelor cu FLUENT. Vol. II: Aplicații în dinamica biofluidelor, Editura Politehnica Press, 2011. ISBN 973-7838-06-8.
Bibliografie suplimentară[modificare | modificare sursă]
- en John D. Anderson, Computational Fluid Dynamics: The Basics With Applications, McGraw-Hill Science, 1995, ISBN 0070016852
Legături externe[modificare | modificare sursă]
 Materiale media legate de Mecanica fluidelor numerică la Wikimedia Commons
Materiale media legate de Mecanica fluidelor numerică la Wikimedia Commons- en CFD-Wiki
- en Dmitri Kuzmin, Introduction to CFD (curs), Universitatea Tehnică din Dortmund
- en Listă de aplicații pentru MFN Arhivat în , la Wayback Machine. (libere, respectiv comerciale)




















![{\displaystyle \rho {\frac {\partial {\bar {u}}_{j}{\bar {u}}_{i}}{\partial x_{j}}}=\rho {\bar {f}}_{i}+{\frac {\partial }{\partial x_{j}}}\left[-{\bar {p}}\delta _{ij}+\mu \left({\frac {\partial {\bar {u}}_{i}}{\partial x_{j}}}+{\frac {\partial {\bar {u}}_{j}}{\partial x_{i}}}\right)-\rho {\overline {u_{i}^{\prime }u_{j}^{\prime }}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e6db087ae802dba0be2ebf9f2d53303f3b4d4b2)






































