Dreaptă

| Geometrie |
|---|
 |
|
|
Cvadri- și n-dimensional |
În matematică o dreaptă este o figură geometrică ce are doar o dimensiune, lungimea. Orice dreaptă este de lungime infinită, conține o infinitate de puncte, este de grosime zero și este o curbă perfect "dreaptă". În geometria euclidiană, pentru două puncte fixe există o dreaptă și numai una ce trece prin amândouă. Este o noțiune primitivă a geometriei. Folosită standard, dreapta reprezintă drumul cel mai scurt dintre două puncte.
Generalități[modificare | modificare sursă]
În cazul bidimensional, două drepte diferite pot fi confundate (dacă au toate punctele comune), paralele (dacă sunt disjuncte, adică nu au nici un punct comun) sau concurente (se intersectează, întotdeauna într-un punct și numai unul). În cazurile tri- sau multidimensionale, dreptele pot fi oarecare între ele, însemnând nu numai că nu se intersectează, dar și că nu definesc un plan. Două plane distincte se pot intersecta după o dreaptă comună. Trei sau mai multe puncte care aparțin uneia și aceleiași drepte se numesc coliniare.
Exemple[modificare | modificare sursă]
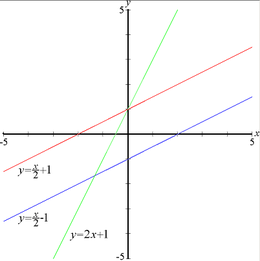
Dreptele dintr-un plan cartezian pot fi definite algebric prin ecuații liniare și funcții liniare. În cazul bi-dimensional, forma cea mai des utilizată este ecuația dreptei în care variabila dependentă (aici, y) este exprimată în "funcție de" variabila independentă (aici, x).
unde
- a este panta dreptei, adică valoarea funcției tangentă a unghiului dintre dreaptă și sensul pozitiv al abscisei (axa orizontală, Ox).
- b este ordonata la origine (distanța măsurată pe axa verticală, 0y, dintre punctul de intersecție al dreptei cu axa 0y și originea sistemului de coordonate.
- x este variabila independentă.
În cazul tridimensional, orice dreaptă este adesea descrisa ca 0y + at
unde
- x, y și z sunt funcții depinzând de aceeași variabilă independentă, t.
- , și reprezintă valorile inițiale ale respectivelor variabile.
- iar a, b și c sunt valori numerice referitoare la panta dreptei, astfel încât vectorul dat de versorii (a, b, c) este paralel cu dreapta.







