4-politop uniform

În geometrie un 4-politop uniform este un politop cvadridimensional izogonal, ale cărui celule sunt poliedre uniforme iar fețele sale sunt poligoane regulate.

Au fost descrise patruzeci și șapte de politopuri uniforme convexe neprismatice, o mulțime finită de forme prismatice convexe și două mulțimi infinite de forme prismatice convexe. Există, de asemenea, un număr necunoscut de forme neconvexe stelate.

Istoria descoperirilor[modificare | modificare sursă]

4-politopurile regulate convexe

În 1852 Ludwig Schläfli a demonstrat în manuscrisul său, Theorie der vielfachen Kontinuität (în română Teoria continuității multiple) că există exact 6 4-politopuri regulate și doar câte 3 în 5 sau mai multe dimensiuni.

4-politopuri stelate regulate

Tot în 1852 Ludwig Schläfli a găsit 4 din cele 10 4-politopuri stelate regulate, fără a număra pe cele 6 cu celule sau figura vârfului {⁵/₂,5} și {5,⁵/₂}.

În 1883 Edmund Hess în cartea sa Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder (în română Introducere în teoria divizării bilelor cu o considerație specială asupra aplicării sale la teoria poliedrelor izoedrice și izogonale) a completat lista celor 10 4-politopuri neconvexe regulate.^[1]

4-politopurile semiregulate convexe

Politopurile semiregulate convexe au avut diferite definiții înainte de definirea categoriei uniforme de către Coxeter.

În 1900 Thorold Gosset în lucrarea sa On the Regular and Semi-Regular Figures in Space of n Dimensions (în română Despre figurile regulate și semiregulate în spațiul cu n dimensiuni) a enumerat lista de politopuri convexe semiregulate neprismatice cu celule regulate (adică poliedre platonice).^[2]

În 1910 Alicia Boole Stott, în lucrarea sa Geometrical deduction of semiregular from regular polytopes and space fillings, (în {{ro|Deducerea geometrică a politopurilor semiregulate din cele regulate și cele care umplu spațiul”, a extins definiția, acceptând și celulele de forma poliedrelor arhimedice și cele prismatice. În urma acestei relaxări a enumerat 45 de 4-politopuri semiregulate.^[3]

În 1911 Pieter Hendrik Schoute a publicat lucrarea Analytic treatment of the polytopes regularly derived from the regular polytopes (în română Tratarea analitică a politopurilor derivate regulat din politopurile regulate), urmat de Boole-Stott, care a notat și enumerat politopurile uniforme convexe în funcție de simetrie, bazat pe 5-celule, 8-celule/16-celule și 24-celule.

În 1912 E. L. Elte a extins independent lista lui Gosset în lucrarea The Semiregular Polytopes of the Hyperspaces (în română Politopurile semiregulate din hiperspații, politopuri cu unul sau două tipuri de fațete semiregulate.^[4]

4-politopurile uniforme convexe

În 1940 căutarea a fost extinsă sistematic de H.S.M. Coxeter în lucrarea sa Regular and Semi-Regular Polytopes (în română Politopuri regulate și semiregulate)

În 1965 John Horton Conway și Michael Guy au publicat în lucrarea lor Four-Dimensional Archimedean Polytopes (în română Politopuri arhimedice cvadridimensionale) lista completă a politopurilor convexe, stabilită prin analiză pe calculator, având și un 4-politop convex newythoffian, marea antiprismă.

În 1966 Norman Johnson în teza sa de doctorat The Theory of Uniform Polytopes and Honeycombs (în română Teoria politopurilor și fagurilor uniformi) elaborată sub conducerea lui Coxeter a completat teoria de bază a politopurilor uniforme din dimensiunile 4 și superioare.

În1986 Coxeter a publicat articolul Regular and Semi-Regular Polytopes II care cuprinde analiza structurii unice a24-celule snub și a simetriei anormalei mari antiprisme.

În 2004 Marco Möller în teza sa de doctorat Vierdimensionale Archimedische Polytope (în română Politopuri arhimedice cvadridimesnionale a dat o demonstrație că setul Conway–Guy este complet.^[5]

În 2008 Conway în The Symmetries of Things (în română Simetriile lucrurilor)^[6] a publicat prima listă tipărită a 4-politopurilor uniforme convexe și a politopurilor din dimensiuni superioare din familia grupului Coxeter, cu diagrame generale ale figurilor vârfurilor pentru fiecare permutare inelată din diagramele Coxeter — snub, marea antiprismă și duoprisme — pe care le-a numit proprisme pentru prismele produsului. El și-a folosit propria schemă de denumire ijk-ambo pentru permutările inelului indexat dincolo de trunchiere și bitrunchiere, iar toate numele lui Johnson au fost incluse în indexul cărții.

4-politopurile stelate uniforme neregulate

Până în 2005, într-o cercetare în colaborare, Jonathan Bowers și George Olshevsky au identificat 1845 de 4-politopuri uniforme (convexe și neconvexe),^[7] iar în 2006 au mai identificat 4.^[8]

Până în 2020–2021 au mai fost descoperite 339 de politopuri noi, ridicând totalul 4-politopurilor uniforme cunoscute la 2188.^[9]

4-politopuri regulate[modificare | modificare sursă]

Articol principal: 4-politop regulat.

4-politopurile regulate sunt un subset al 4-politopurilor uniforme, care îndeplinesc cerințe suplimentare. 4-politopurile regulate sunt descrise de simbolurile Schläfli {p,q,r}, au celule de tipul {p,q}, fețe de tipul {p}, laturi de tipul {r}, și figuri ale vârfului de tipul {q,r}.

Existența unui 4-politop regulat {p,q,r} este condiționată de existența poliedrelor regulate {p,q}, care va fi celulele și {q,r} care va fi figura vârfului.

Existența unui 4-politop finit este condiționată de inegalitatea:^[10]

\sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)>\cos \left({\frac {\pi }{q}}\right).

Cele 16 4-politopuri regulate, având proprietatea că toate celulele, fețele, laturile și vârfurile sunt congruente sunt:

6 4-politopuri regulate convexe: 5-celule {3,3,3}, 8-celule {4,3,3}, 16-celule {3,3,4}, 24-celule {3,4,3}, 120-celule {5,3,3} și 600-celule {3,3,5}.
10 4-politopuri regulate stelate: 120-celule icosaedric {3,5,⁵/₂}, micul 120-celule stelat {⁵/₂,5,3}, marele 120-celule {5,⁵/₂,5}, largul 120-celule {5,3,⁵/₂}, marele 120-celule stelat {⁵/₂,3,5}, largul 120-celule stelat {⁵/₂,5,⁵/₂}, marele larg 120-celule {5,⁵/₂,3}, marele 120-celule icosaedric {3,⁵/₂,5}, largul 600-celule {3,3,⁵/₂} și marele larg 120-celule stelat {⁵/₂,3,3}.

4-politopuri uniforme convexe[modificare | modificare sursă]

Simetria 4-politopurilor uniforme în patru dimensiuni[modificare | modificare sursă]

Subgrupuri ortogonale
Cele 16 oglinzi ale B₄ pot fi descompuse în două grupuri ortogonale, 4A₁ și D₄: = (4 oglinzi) = (12 oglinzi)
Cele 24 oglinzi ale F₄ pot fi descompuse în două grupuri ortogonale, D₄: = (12 oglinzi) = (12 oglinzi)
Cele 10 oglinzi ale B₃×A₁ pot fi descompuse în grupurile ortogonale 4A₁ și D₃: = (3+1 oglinzi) = (6 oglinzi)

Există 5 familii fundamentale de grupuri punctuale de simetrii în oglindă în 4-dimensiuni: A₄ = , B₄ = , D₄ = , F₄ = , H₄ = .^[11] Există și 3 grupuri prismatice: A₃A₁ = , B₃A₁ = , H₃A₁ = și grupurile duoprismatice: I₂(p)×I₂(q) = . Fiecare grup este definit pe domeniul fundamental al unui tetraedru Goursat delimitat de plane de reflexie.

Orice 4-politop uniform construit prin reflexii face parte dintr-unul sau mai multe grupuri punctuale de reflexii în 4 dimensiuni printr-o construcție Wythoff, caracterizată de inele în jurul permutărilor nodurilor într-o diagramă Coxeter. Hiperplanele oglinzilor pot fi grupate folosind noduri colorate separate prin ramuri pare. Grupurile de simetrie de forma [a,b,a], au o simetrie extinsă, [[a,b,a]], dublând ordinul de simetrie. Acestea includ [3,3,3], [3,4,3] și [p,2,p]. Politopurile uniforme din acest grup cu inele simetrice conțin această simetrie extinsă.

Dacă într-un politop uniform dat toate oglinzile de o anumită culoare sunt neinelate (inactive), acesta va avea un ordin de simetrie mai mic prin eliminarea tuturor oglinzilor inactive. Dacă toate nodurile unei anumite culori sunt inelate (active), operatorul alternare poate genera un nou 4-politop cu simetrie chirală, prezentat ca „noduri goale încercuite”, dar geometria nu este întotdeauna susceptibilă de a crea soluții uniforme.

Grup Weyl	Cuaternion Conway	Structură abstractă	Ordin	Notație Coxeter	Subgrup comutator	Număr Coxeter (h)	Oglinzi m=2h
Ireductibile
A₄	+1/60[I×I].21	S₅	120	[3,3,3]	[3,3,3]⁺	5		10
D₄	±1/3[T×T].2	1/2.²S₄	192	[3^1,1,1]	[3^1,1,1]⁺	6		12
B₄	±1/6[O×O].2	²S₄ = S₂≀S₄	384	[4,3,3]	[3^1,1,1]⁺	8	4	12
F₄	±1/2[O×O].2₃	3.²S₄	1152	[3,4,3]	[3⁺,4,3⁺]	12	12	12
H₄	±[I×I].2	2.(A₅×A₅).2	14400	[5,3,3]	[5,3,3]⁺	30		60
Grupuri prismatice
A₃A₁	+1/24[O×O].2₃	S₄×D₁	48	[3,3,2] = [3,3]×[ ]	[3,3]⁺	-		6	1
B₃A₁	±1/24[O×O].2	S₄×D₁	96	[4,3,2] = [4,3]×[ ]	[3,3]⁺	-	3	6	1
H₃A₁	±1/60[I×I].2	A₅×D₁	240	[5,3,2] = [5,3]×[ ]	[5,3]⁺	-		15	1
Grupuri duoprismatice (Use 2p,2q pentru întregi pari)
I₂(p)I₂(q)	±1/2[D_2p×D_2q]	D_p×D_q	4pq	[p,2,q] = [p]×[q]	[p⁺,2,q⁺]	-		p	q
I₂(2p)I₂(q)	±1/2[D_4p×D_2q]	D_2p×D_q	8pq	[2p,2,q] = [2p]×[q]		-	p	p	q
I₂(2p)I₂(2q)	±1/2[D_4p×D_4q]	D_2p×D_2q	16pq	[2p,2,2q] = [2p]×[2q]		-	p	p	q	q

Enumerare[modificare | modificare sursă]

Există 64 de politopuri uniforme convexe, inclusiv cele 6 politopuri convexei regulate, excluzând mulțimile infinite ale duoprismelor și ale prismelor antiprismatice.

5 sunt prisme poliedrice bazate pe poliedrele platonice s (1 se suprapune cu cele regulate, deoarece o hiperprismă cubică este un tesseract)
13 sunt prisme poliedrice bazate pe poliedrele arhimedice
9 sunt în familia grupului autodual regulat A₄ [3,3,3] din familia 5-celule
9 sunt în grupul autodual regulat F₄ [3,4,3] din familia 24-celule (fără 24-celule snub)
15 sunt în grupul regulat B₄ [3,3,4] din familia tesseract/16-celule (3 se suprapun cu camilia 24-celule)
15 sunt în grupul regulat H₄ [3,3,5] din familia 120-celule/600-celule.
1 caz particular snub din grupul [3,4,3] din familia 24-celule.
1 caz particular newythoffian, marea antiprismă.

TOTAL: 68 − 4 = 64

Aceste 64 de politopuri uniforme sunt enumerate mai jos de George Olshevsky. Formele de simetrie repetate sunt indicate între paranteze.

În plus față de cele 64 de mai sus există 2 mulțimi prismatice infinite care generează toate formele convexe rămase:

Mulțimea hiperprismelor antiprismatice uniforme — sr{p,2}×{ } — prisme poliedrice de două antiprisme.
Mulțimea duoprismelor uniforme — {p}×{q} — produsul cartezian al două poligoane.

Familia A₄[modificare | modificare sursă]

5-celule are simetrie 4-simplectică [3,3,3],^[11] de ordinul 120, izomorfă cu permutările a cinci elemente, deoarece toate perechile de vârfuri sunt legate în același mod.

Fațetele (celulele) sunt date, grupate în pozițiile lor din diagrama Coxeter, prin eliminarea nodurilor specificate.

Politopuri uniforme [3,3,3]
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție				Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (5)	Poz. 2 (10)	Poz. 1 (10)	Poz. 0 (5)	Celule	Fețe	Laturi	Vârfuri
1	5-celule^[11]		{3,3,3}	(4) (3.3.3)				5	10	10	5
2	5-celule rectificat		r{3,3,3}	(3) (3.3.3.3)			(2) (3.3.3)	10	30	30	10
3	5-celule trunchiat		t{3,3,3}	(3) (3.6.6)			(1) (3.3.3)	10	30	40	20
4	5-celule cantelat		rr{3,3,3}	(2) (3.4.3.4)		(2) (3.4.4)	(1) (3.3.3.3)	20	80	90	30
7	5-celule cantitrunchiat		tr{3,3,3}	(2) (4.6.6)		(1) (3.4.4)	(1) (3.6.6)	20	80	120	60
8	5-celule runcitrunchiat		t_0,1,3{3,3,3}	(1) (3.6.6)	(2) (4.4.6)	(1) (3.4.4)	(1) (3.4.3.4)	30	120	150	60

Politopuri uniforme [[3,3,3]]
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție			Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3-0 (10)	Poz. 1-2 (20)	Alt	Celule	Fețe	Laturi	Vârfuri
5	*5-celule runcinat		t_0,3{3,3,3}	(2) (3.3.3)	(6) (3.4.4)		30	70	60	20
6	*5-celule bitrunchiat		2t{3,3,3}	(4) (3.6.6)			10	40	60	30
9	*5-celule omnitrunchiat		t_0,1,2,3{3,3,3}	(2) (4.6.6)	(2) (4.4.6)		30	150	240	120
Neuniform	5-celule omnisnub^[12]		ht_0,1,2,3{3,3,3}	(2) (3.3.3.3.3)	(2) (3.3.3.3)	(4) (3.3.3)	90	300	270	60

Cele trei forme de 4-politopuri uniforme marcate cu un asterisc, *, au cea mai mare simetrie 4-tetraedrică extinsă, de ordinul 240, [[3,3,3]] deoarece elementul corespunzător oricărui element al 5-celulei de bază poate fi schimbat cu unul dintre cele corespunzătoare unui element al dualului său. Există un mic subgrup indice [3,3,3]⁺, de ordin 60, sau dublul acestuia [[3,3,3]]⁺, de ordin 120, definind un 5 celule omnisnub care este listat pentru completare, dar nu este uniform.

Familia B₄[modificare | modificare sursă]

Această familie are simetrie 4-ortoplectică [4,3,3],^[11] de ordinul 24 × 16 = 384: 4! = 24 permutări ale celor 4 axe, respectiv 2⁴ = 16 reflexii față de fiecare axă. Există 3 mici subgrupuri indice, dintre care primele două generează 4-politopuri uniforme care se repetă și în alte familii, [1⁺,4,3,3], [4,(3,3)⁺] și [4,3,3]⁺, toate de ordinul 192.

Trunchieri ale tesseractului[modificare | modificare sursă]

Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție					Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (8)	Poz. 2 (24)	Poz. 1 (32)	Poz. 0 (16)	Celule	Fețe	Laturi	Vârfuri
10	tesseract sau 8-celule		{4,3,3}	(4) (4.4.4)				8	24	32	16
11	Tesseract rectificat	r{4,3,3}	(3) (3.4.3.4)			(2) (3.3.3)	24	88	96	32
13	Tesseract trunchiat		t{4,3,3}	(3) (3.8.8)			(1) (3.3.3)	24	88	128	64
14	Tesseract cantelat		rr{4,3,3}	(1) (3.4.4.4)		(2) (3.4.4)	(1) (3.3.3.3)	56	248	288	96
15	Tesseract runcinat (și 16-celule runcinat)		t_0,3{4,3,3}	(1) (4.4.4)	(3) (4.4.4)	(3) (3.4.4)	(1) (3.3.3)	80	208	192	64
16	Tesseract bitrunchiat (și 16-celule bitrunchiat)		2t{4,3,3}	(2) (4.6.6)			(2) (3.6.6)	24	120	192	96
18	Tesseract cantitrunchiat		tr{4,3,3}	(2) (4.6.8)		(1) (3.4.4)	(1) (3.6.6)	56	248	384	192
19	Tesseract runcitrunchiat		t_0,1,3{4,3,3}	(1) (3.8.8)	(2) (4.4.8)	(1) (3.4.4)	(1) (3.4.3.4)	80	368	480	192
21	Tesseract omnitrunchiat (și 16-celule omnitrunchiat)		t_0,1,2,3{3,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.6)	(1) (4.6.6)	80	464	768	384

4-politopuri uniforme asociate cu semitesseractul, [1⁺,4,3,3]
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție					Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (8)	Poz. 2 (24)	Poz. 1 (32)	Poz. 0 (16)	Alt	Celule	Fețe	Laturi	Vârfuri
12	Semitesseract 16-celule		= h{4,3,3}={3,3,4}	(4) (3.3.3)				(4) (3.3.3)	16	32	24	8
[17]	Tesseract cantic (sau 16-celule trunchiat)		= h₂{4,3,3}=t{4,3,3}	(4) (6.6.3)			(1) (3.3.3.3)		24	96	120	48
[11]	Tesseract runcic (sau tesseract rectificat)		= h₃{4,3,3}=r{4,3,3}	(3) (3.4.3.4)			(2) (3.3.3)		24	88	96	32
[16]	Tesseract runcicantic (sau tesseract bitrunchiat)		= h_2,3{4,3,3}=2t{4,3,3}	(2) (3.4.3.4)			(2) (3.6.6)		24	120	192	96
[11]	(Tesseract rectificat)		= h₁{4,3,3}=r{4,3,3}						24	88	96	32
[16]	(Tesseract bitrunchiat)		= h_1,2{4,3,3}=2t{4,3,3}						24	120	192	96
[23]	(24-celule rectificat)		= h_1,3{4,3,3}=rr{3,3,4}						48	240	288	96
[24]	(24-celule trunchiat)		= h_1,2,3{4,3,3}=tr{3,3,4}						48	240	384	192

Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție					Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (8)	Poz. 2 (24)	Poz. 1 (32)	Poz. 0 (16)	Alt	Celule	Fețe	Laturi	Vârfuri
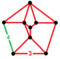
Neuniform	Tesseract omnisnub^[13] (sau 16-celule omnisnub)		ht_0,1,2,3{4,3,3}	(1) (3.3.3.3.4)	(1) (3.3.3.4)	(1) (3.3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)	272	944	864	192

Trunchieri ale 16-celulei[modificare | modificare sursă]

Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție					Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (8)	Poz. 2 (24)	Poz. 1 (32)	Poz. 0 (16)	Alt	Celule	Fețe	Laturi	Vârfuri
[12]	16-celule^[11]		{3,3,4}				(8) (3.3.3)		16	32	24	8
[22]	16-celule rectificat (același cu 24-celule*)		= r{3,3,4}	(2) (3.3.3.3)			(4) (3.3.3.3)		24	96	96	24
17	16-celule trunchiat		t{3,3,4}	(1) (3.3.3.3)			(4) (3.6.6)		24	96	120	48
[23]	16-celule cantelat (același cu 24-celule rectificat*)		= rr{3,3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.3.4)		48	240	288	96
[15]	16-celule runcinat (și 8-celule runcinat)		t_0,3{3,3,4}	(1) (4.4.4)	(3) (4.4.4)	(3) (3.4.4)	(1) (3.3.3)		80	208	192	64
[16]	16-celule bitrunchiat (și 8-celule bitrunchiat)		2t{3,3,4}	(2) (4.6.6)			(2) (3.6.6)		24	120	192	96
[24]	16-celule cantitrunchiat (același cu 24-celule trunchiat*)		= tr{3,3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.6)		48	240	384	192
20	16-celule runcitrunchiat		t_0,1,3{3,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.6)	(1) (3.6.6)		80	368	480	192
[21]	16-celule omnitrunchiat (și 8-celule omnitrunchiat)		t_0,1,2,3{3,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.6)	(1) (4.6.6)		80	464	768	384
[31]	16-celule cantitrunchiat alternat (același cu 24-celule snub)		sr{3,3,4}	(1) (3.3.3.3.3)		(1) (3.3.3)	(2) (3.3.3.3.3)	(4) (3.3.3)	144	480	432	96
Neuniform	16-celule rectificat runcic snub		sr₃{3,3,4}	(1) (3.4.4.4)	(2) (3.4.4)	(1) (4.4.4)	(1) (3.3.3.3.3)	(2) (3.4.4)	176	656	672	192

(*) Așa cum rectificarea tetraedrului produce octaedrul, rectificarea 16-celulei produce 24-celule, membru regulat al familiei următoare.

24-celule snub este repetat în această familie pentru completitudine. Este o alternare a 16-celule cantitrunchiat sau 24-celule trunchiat, cu grupul jumătății de simetrie [(3,3)⁺,4]. Celulele octaedrice trunchiate devin icosaedre. Cuburile devin tetraedre, iar 96 de tetraedre noi sunt create în golurile lăsate de vârfurile eliminate.

Familia F₄[modificare | modificare sursă]

Acestă familie are simetrie octaplectică,^[11] [3,4,3], de ordinul 24 × 48 = 1152: cele 48 de simetrii ale octaedrului pentru fiecare din cele 24 de celule. Există 3 mici subgrupuri indice, dintre care primele două generează 4-politopuri uniforme care se repetă și în alte familii, [3⁺,4,3], [3,4,3⁺] și [3,4,3]⁺, toate de ordinul 576.

4-politopuri uniforme [3,4,3]
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție				Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (24)	Poz. 2 (96)	Poz. 1 (96)	Poz. 0 (24)	Celule	Fețe	Laturi	Vârfuri
22	24-celule^[11] (același cu 16-celule rectificat)		{3,4,3}	(6) (3.3.3.3)				24	96	96	24
23	24-celule rectificat (același cu 16-celule cantelat)		r{3,4,3}	(3) (3.4.3.4)			(2) (4.4.4)	48	240	288	96
24	24-celule trunchiat (același cu 16-celule cantitrunchiat)		t{3,4,3}	(3) (4.6.6)			(1) (4.4.4)	48	240	384	192
25	24-celule cantelat		rr{3,4,3}	(2) (3.4.4.4)		(2) (3.4.4)	(1) (3.4.3.4)	144	720	864	288
28	24-celule cantitrunchiat		tr{3,4,3}	(2) (4.6.8)		(1) (3.4.4)	(1) (3.8.8)	144	720	1152	576
29	24-celule runcitrunchiat		t_0,1,3{3,4,3}	(1) (4.6.6)	(2) (4.4.6)	(1) (3.4.4)	(1) (3.4.4.4)	240	1104	1440	576

4-politopuri uniforme [3⁺,4,3]
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție					Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (24)	Poz. 2 (96)	Poz. 1 (96)	Poz. 0 (24)	Alt	Celule	Fețe	Laturi	Vârfuri
31	24-celule snub^†		s{3,4,3}	(3) (3.3.3.3.3)			(1) (3.3.3)	(4) (3.3.3)	144	480	432	96
Neuniform	24-celule snub runcic		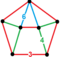s₃{3,4,3}	(1) (3.3.3.3.3)	(2) (3.4.4)		(1) (3.6.6)	(3) Tricup	240	960	1008	288
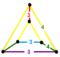
[25]	24-celule snub cantic (același cu 24-celule cantelat)		s₂{3,4,3}	(2) (3.4.4.4)			(1) (3.4.3.4)	(2) (3.4.4)	144	720	864	288
[29]	24-celule snub runcicantic (același cu 24-celule runcitrunchiat)		s_2,3{3,4,3}	(1) (4.6.6)		(1) (3.4.4)	(1) (3.4.4.4)	(2) (4.4.6)	240	1104	1440	576

^† Aici 24-celule snub, în ciuda numelui său comun, nu este analog cu cubul snub; mai degrabă este derivat printr-o alternare a 24-celule trunchiat. Ordinul său de simetrie este de numai 576, (grupul [3⁺,4,3]).

Ca și 5-celule, 24-celule este autodual, astfel că următoarele trei forme au de două ori mai multe simetrii, în total 2304 ([[3,4,3]]).

4-politopuri uniforme [[3,4,3]]
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Nr. celulelor din poziție		Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3-0 (48)	Poz. 2-1 (192)	Celule	Fețe	Laturi	Vârfuri
26	24-celule runcinat		t_0,3{3,4,3}	(2) (3.3.3.3)	(6) (3.4.4)	240	672	576	144
27	24-celule bitrunchiat		2t{3,4,3}	(4) (3.8.8)		48	336	576	288
30	24-celule omnitrunchiat		t_0,1,2,3{3,4,3}	(2) (4.6.8)	(2) (4.4.6)	240	1392	2304	1152

4-politopuri izogonale [[3,4,3]]⁺
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție			Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3-0 (48)	Poz. 2-1 (192)	Alt	Celule	Fețe	Laturi	Vârfuri
Neuniform	24-celule omnisnub^[14]		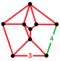ht_0,1,2,3{3,4,3}	(2) (3.3.3.3.4)	(2) (3.3.3.3)	(4) (3.3.3)	816	2832	2592	576

Familia H₄[modificare | modificare sursă]

Această familie are simetrie dodecaplectică,^[11] [5,3,3], de ordinul 120 × 120 = 24 × 600 = 14400: 120 pentru fiecare din cele 120 de dodecaedre, sau 24 pentru fiecare din cele 600 de tetraedre. Există un mic subgrup indice, [5,3,3]⁺, toate de ordinul 7200.

Trunchieri ale 120-celulei[modificare | modificare sursă]

Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție					Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Poz. 3 (120)	Poz. 2 (720)	Poz. 1 (1200)	Poz. 0 (600)	Alt	Celule	Fețe	Laturi	Vârfuri
32	120-celule^[11]		{5,3,3}	(4) (5.5.5)					120	720	1200	600
33	120-celule rectificat		r{5,3,3}	(3) (3.5.3.5)			(2) (3.3.3)		720	3120	3600	1200
36	120-celule trunchiat		t{5,3,3}	(3) (3.10.10)			(1) (3.3.3)		720	3120	4800	2400
37	120-celule cantelat		rr{5,3,3}	(1) (3.4.5.4)		(2) (3.4.4)	(1) (3.3.3.3)		1920	9120	10800	3600
38	120-celule runcinat (și 600-celule runcinat)		t_0,3{5,3,3}	(1) (5.5.5)	(3) (4.4.5)	(3) (3.4.4)	(1) (3.3.3)		2640	7440	7200	2400
39	120-celule bitrunchiat (și 600-celule bitrunchiat)		2t{5,3,3}	(2) (5.6.6)			(2) (3.6.6)		720	4320	7200	3600
42	120-celule cantitrunchiat		tr{5,3,3}	(2) (4.6.10)		(1) (3.4.4)	(1) (3.6.6)		1920	9120	14400	7200
43	120-celule runcitrunchiat		t_0,1,3{5,3,3}	(1) (3.10.10)	(2) (4.4.10)	(1) (3.4.4)	(1) (3.4.3.4)		2640	13440	18000	7200
46	120-celule omnitrunchiat (și 600-celule omnitrunchiat)		t_0,1,2,3{5,3,3}	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.6)	(1) (4.6.6)		2640	17040	28800	14400
Neuniform	120-celule omnisnub^[15] (același cu 600-celule omnisnub)		ht_0,1,2,3{5,3,3}	(1) (3.3.3.3.5)	(1) (3.3.3.5)	(1) (3.3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)	9840	35040	32400	7200

Trunchieri ale 600-celulei[modificare | modificare sursă]

Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Simetrie	Numărul. celulelor din poziție				Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Simetrie	Poz. 3 (120)	Poz. 2 (720)	Poz. 1 (1200)	Poz. 0 (600)	Celule	Fețe	Laturi	Vârfuri
35	600-celule^[11]		{3,3,5}	[5,3,3] ordin 14400				(20) (3.3.3)	600	1200	720	120
[47]	600-celule 20-diminuat (marea antiprismă)		Construcție newythoffiană	[[10,2⁺,10]] ordin 400 indice 36	(2) (3.3.3.5)			(12) (3.3.3)	320	720	500	100
[31]	600-celule 24-diminuat (24-celule snub)		Construcție newythoffiană	[3⁺,4,3] order 576 index 25	(3) (3.3.3.3.3)			(5) (3.3.3)	144	480	432	96
Nonuniform	600-celule bi-24-diminuat		Construcție newythoffiană	ordin 144 index 100	(6) tdi				48	192	216	72
34	600-celule rectificat		r{3,3,5}	[5,3,3]	(2) (3.3.3.3.3)			(5) (3.3.3.3)	720	3600	3600	720
Neuniform	600-celule rectificat 120-diminuat		Construcție newythoffiană	ordin 1200 index 12	(2) 3.3.3.5	(2) 4.4.5		(5) P4	840	2640	2400	600
41	600-celule trunchiat		t{3,3,5}	[5,3,3]	(1) (3.3.3.3.3)			(5) (3.6.6)	720	3600	4320	1440
40	600-celule cantelat		rr{3,3,5}	[5,3,3]	(1) (3.5.3.5)	(2) (4.4.5)		(1) (3.4.3.4)	1440	8640	10800	3600
[38]	600-celule runcinat (și 120-celule runcinat)		t_0,3{3,3,5}	[5,3,3]	(1) (5.5.5)	(3) (4.4.5)	(3) (3.4.4)	(1) (3.3.3)	2640	7440	7200	2400
[39]	600-celule bitrunchiat (și 120-celule bitrunchiat)		2t{3,3,5}	[5,3,3]	(2) (5.6.6)			(2) (3.6.6)	720	4320	7200	3600
45	600-celule cantitrunchiat		tr{3,3,5}	[5,3,3]	(1) (5.6.6)	(1) (4.4.5)		(2) (4.6.6)	1440	8640	14400	7200
44	600-celule runcitrunchiat		t_0,1,3{3,3,5}	[5,3,3]	(1) (3.4.5.4)	(1) (4.4.5)	(2) (4.4.6)	(1) (3.6.6)	2640	13440	18000	7200
[46]	600-celule omnitrunchiat (și 120-celule omnitrunchiat)		t_0,1,2,3{3,3,5}	[5,3,3]	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.6)	(1) (4.6.6)	2640	17040	28800	14400

Familia D₄[modificare | modificare sursă]

Familia semitesseractelor, [3^1,1,1], nu produce noi 4-politopuri uniforme, ci repetă unele construcții alternative. Familia are simetrii de ordinul 12 × 16 = 192: 4!/2 = 12 permutatări ale celor patru axe, alternate la jumătate, 2⁴ = 16 de reflexii față de fiecare axă. Există un mic subgrup indice care formează 4-politopuri, [3^1,1,1]⁺, de ordinul 96.

4-politopuri uniforme [3^1,1,1]
Nr.	Nume	Figura vârfului	Diagramă Coxeter = =	Numărul celulelor din poziție					Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter = =	Poz. 0 (8)	Poz. 2 (24)	Poz. 1 (8)	Poz. 3 (8)	Poz. alt (96)	Celule	Fețe	Laturi	Vârfuri
[12]	Semitesseract (același cu 16-celule)		= h{4,3,3}			(4) (3.3.3)	(4) (3.3.3)		16	32	24	8
[17]	tesseract cantic (același cu 16-celule trunchiat)		= h₂{4,3,3}	(1) (3.3.3.3)		(2) (3.6.6)	(2) (3.6.6)		24	96	120	48
[11]	tesseract runcic (același cu tesseract rectificat)		= h₃{4,3,3}	(1) (3.3.3)		(1) (3.3.3)	(3) (3.4.3.4)		24	88	96	32
[16]	tesseract runcicantic (același cu tesseract bitrunchiat)		= h_2,3{4,3,3}	(1) (3.6.6)		(1) (3.6.6)	(2) (4.6.6)		24	96	96	24

Când nodurile celor 3 ramuri bifurcate sunt inelate identic, simetria poate fi mărită cu 6, ca [3[3^1,1,1]] = [3,4,3], astfel aceste politopuri sunt repetări din familia 24-celule.

4-politopuri uniforme [3[3^1,1,1]]
Nr.	Nume	Figura vârfului	Diagramă Coxeter = =	Numărul celulelor din poziție			Numărul elementelor
Nr.	Nume	Figura vârfului	Diagramă Coxeter = =	Poz. 0,1,3 (24)	Poz. 2 (24)	Poz. alt (96)	Celule	Fețe	Laturi	Vârfuri
[22]	16-celule rectificat (același cu 24-celule)		= = = {3^1,1,1} = r{3,3,4} = {3,4,3}	(6) (3.3.3.3)			48	240	288	96
[23]	16-celule cantelat (același cu 24-celule rectificat)		= = = r{3^1,1,1} = rr{3,3,4} = r{3,4,3}	(3) (3.4.3.4)	(2) (4.4.4)		24	120	192	96
[24]	16-celule cantitrunchiat (același cu 24-celule trunchiat)		= = = t{3^1,1,1} = tr{3,3,4} = t{3,4,3}	(3) (4.6.6)	(1) (4.4.4)		48	240	384	192
[31]	24-celule snub		= = = s{3^1,1,1} = sr{3,3,4} = s{3,4,3}	(3) (3.3.3.3.3)	(1) (3.3.3)	(4) (3.3.3)	144	480	432	96

Și aici, 24-celule snub, cu grupul de simetrie [3^1,1,1]⁺, reprezintă o trunchiere alternată a 24-celule trunchiat, cu 96 de noi tetraedre în pozițiile vârfurilor șterse. Spre deosebire de apariția sa în celelalte grupuri, ca 4-politop parțial snub, numai în cadrul acestui grup de simetrie este complet analog cu snuburile Kepler, adică cubul snub și dodecaedrul snub.

Marea antiprismă[modificare | modificare sursă]

Marea antiprismă este un 4-politop convex uniform newythoffian format din 20 de antiprisme pentagonale care formează două inele perpendiculare unite prin 300 de tetraedrue. Este întrucâtva analog antiprismelor tridimensionale, care constau din două poligoane paralele unite de o bandă de triunghiuri. Însă, spre deosebire de ele, marea antiprismă nu este membrul unei familii infinite de politopuri uniforme.

Simetria sa este grupul Coxeter diminuat ionic, [[10,2⁺,10]], de ordinul 400.

Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Cells by type		Element counts				Net
Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Cells by type		Celule	Fețe	Laturi	Vârfuri	Net
47	Marea antiprismă			Fără simbol	300 (3.3.3)	20 (3.3.3.5)	320	20 {5} 700 {3}	500	100

4-politopuri prismatice uniforme[modificare | modificare sursă]

Un politop prismatic este un produs cartezian din două politopuri din dimensiuni inferioare; exemple familiare sunt [[prismă (geometrie) |prismele] tridimensionale, care sunt produse ale unui poligon și ale unui segment de dreaptă. 4-politopurile uniforme prismatice constau din două familii infinite:

"Prisme poliedrice": produsul unui segment de dreaptă și a unui poliedru uniform. Această familie este infinită deoarece include prismele și antiprismele tridimensionale.
Duoprisme: produsul a două poligoane.

Prisme poliedrice convexe[modificare | modificare sursă]

O familie evidentă de 4-politopuri prismatice este prismele poliedrice, adică produsul unui poliedru cu un segment de dreaptă. Celulele unui astfel de 4-politop sunt două poliedre uniforme identice situate în hiperplane paralele (celulele de bază) și un strat de prisme care le unesc (celulele laterale). Această familie conține prisme pentru cele 75 de poliedre uniforme neprismatice (din care 18 sunt convexe; dintre acestea, una, prisma cub, este prezentată mai sus ca teseract).

Există 18 prisme poliedrice convexe create din cele 5 poliedre platonice și cele 13 poliedre arhimedice, precum și pentru familiile infinite de prisme și antiprisme tridimensionale. Ordinul de simetrie al unei prisme poliedrice este de două ori mai mare decât cel al poliedrului de bază.

Prisme tetraedrice: A₃ × A₁[modificare | modificare sursă]

Acestea au simetrie tetraedrică prismatică [3,3,2], de ordinul 48. Există două subgrupuri indice, [(3,3)⁺,2] și [3,3,2]⁺, dar al doilea nu produce 4-politopuri uniforme.

4-politopuri uniforme [3,3,2]
Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	rowspan=2 colspan=3	Nr. celulelor din poziție	Numărul elementelor				Desfășurată
Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Celule	Fețe	Laturi	Vârfuri			Desfășurată
48	Prismă tetraedrică			{3,3}×{ } t_0,3{3,3,2}	2 3.3.3	4 3.4.4		6	8 {3} 6 {4}	16	8
49	Prismă tetraedrică trunchiată			t{3,3}×{ } t_0,1,3{3,3,2}	2 3.6.6	4 3.4.4	4 4.4.6	10	8 {3} 18 {4} 8 {6}	48	24

4-politopuri uniforme [[3,3],2]</nowiki>
Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	rowspan=2 colspan=3	Nr. celulelor din poziție	Numărul elementelor				Desfășurată
Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Celule	Fețe	Laturi	Vârfuri			Desfășurată
[51]	Prismă tetraedrică rectificată (același cu prismă octaedrică)			r{3,3}×{ } t_1,3{3,3,2}	2 3.3.3.3	4 3.4.4		6	16 {3} 12 {4}	30	12
[50]	Prismă tetraedrică cantelată (același cu prismă cuboctaedrică)			rr{3,3}×{ } t_0,2,3{3,3,2}	2 3.4.3.4	8 3.4.4	6 4.4.4	16	16 {3} 36 {4}	60	24
[54]	Prismă tetraedrică cantitrunchiată (același cu prismă octaedrică trunchiată)			tr{3,3}×{ } t_0,1,2,3{3,3,2}	2 4.6.6	8 6.4.4	6 4.4.4	16	48 {4} 16 {6}	96	48
[59]	Prismă tetraedrică snub (același cu prismă icosaedrică)			sr{3,3}×{ }	2 3.3.3.3.3	20 3.4.4		22	40 {3} 30 {4}	72	24
Neuniform	Antiprismă tetraedrică omnisnub			$s\left\{{\begin{array}{l}3\\3\\2\end{array}}\right\}$	2 3.3.3.3.3	8 3.3.3.3	6+24 3.3.3	40	16+96 {3}	96	24

Prisme octaedrice: B₃ × A₁[modificare | modificare sursă]

Acestea au simetrie octaedrică prismatică [4,3,2], de ordinul 96. Există 6 subgrupuri indice 2, de ordinul 48, care generează 4-politopurile alternate de mai jos. Simetriile, în notația Coxeter sunt [(4,3)⁺,2], [1⁺,4,3,2], [4,3,2⁺], [4,3⁺,2], [4,(3,2)⁺] și [4,3,2]⁺.

Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție				Numărul elementelor				Desfășurată
Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție				Celule	Fețe	Laturi	Vârfuri	Desfășurată
[10]	Prismă cubică (același cu tesseract) (același cu 4-4 duoprismă)			{4,3}×{ } t_0,3{4,3,2}	2 4.4.4	6 4.4.4			8	24 {4}	32	16
50	Prismă cuboctaedrică (același cu prismă tetraedrică cantelată)			r{4,3}×{ } t_1,3{4,3,2}	2 3.4.3.4	8 3.4.4	6 4.4.4		16	16 {3} 36 {4}	60	24
51	prismă octaedrică (același cu prismă tetraerică rectificată) (același cu prismă antiprismatică tringhiulară)			{3,4}×{ } t_2,3{4,3,2}	2 3.3.3.3	8 3.4.4			10	16 {3} 12 {4}	30	12
52	Prismă rombicuboctaedrică			rr{4,3}×{ } t_0,2,3{4,3,2}	2 3.4.4.4	8 3.4.4	18 4.4.4		28	16 {3} 84 {4}	120	48
53	Prismă cubică trunchiată			t{4,3}×{ } t_0,1,3{4,3,2}	2 3.8.8	8 3.4.4	6 4.4.8		16	16 {3} 36 {4} 12 {8}	96	48
54	Prismă octaedrică trunchiată (același cu prismă tetraedrică cantitrunchiată)			t{3,4}×{ } t_1,2,3{4,3,2}	2 4.6.6	6 4.4.4	8 4.4.6		16	48 {4} 16 {6}	96	48
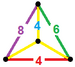
55	Prismă cuboctaedrică trunchiată			tr{4,3}×{ } t_0,1,2,3{4,3,2}	2 4.6.8	12 4.4.4	8 4.4.6	6 4.4.8	28	96 {4} 16 {6} 12 {8}	192	96
56	Prismă cubică snub		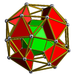	sr{4,3}×{ }	2 3.3.3.3.4	32 3.4.4	6 4.4.4		40	64 {3} 72 {4}	144	48
[48]	Prismă tetraedrică			h{4,3}×{ }	2 3.3.3	4 3.4.4			6	8 {3} 6 {4}	16	8
[49]	Prismă tetraedrică trunchiată			h₂{4,3}×{ }	2 3.3.6	4 3.4.4	4 4.4.6		6	8 {3} 6 {4}	16	8
[50]	Prismă cuboctaedrică			rr{3,3}×{ }	2 3.4.3.4	8 3.4.4	6 4.4.4		16	16 {3} 36 {4}	60	24
[52]	Prismă rombicuboctaedrică			s₂{3,4}×{ }	2 3.4.4.4	8 3.4.4	18 4.4.4		28	16 {3} 84 {4}	120	48
[54]	Prismă octaedrică trunchiată			tr{3,3}×{ }	2 4.6.6	6 4.4.4	8 4.4.6		16	48 {4} 16 {6}	96	48
[59]	Prismă icosaedrică			s{3,4}×{ }	2 3.3.3.3.3	20 3.4.4			22	40 {3} 30 {4}	72	24
[12]	16-celule		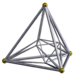	s{2,4,3}	2+6+8 3.3.3.3				16	32 {3}	24	8
Neuniform	Antiprismă tetraedrică omnisnub			sr{2,3,4}	2 3.3.3.3.3	8 3.3.3.3	6+24 3.3.3		40	16+96 {3}	96	24
Neuniform	Antiprismă cubică omnisnub			$s\left\{{\begin{array}{l}4\\3\\2\end{array}}\right\}$	2 3.3.3.3.4	12+48 3.3.3	8 3.3.3.3	6 3.3.3.4	76	16+192 {3} 12 {4}	192	48
Neuniform	4-hosoedru cubic snub runcic			s₃{2,4,3}	2 3.6.6	6 3.3.3	8 cupolă triunghiulară		16	52	60	24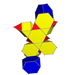

Prisme icosaedrice: H₃ × A₁[modificare | modificare sursă]

Acestea au simetrie icosaedrică prismatică [5,3,2], de ordinul 240. Există două subgrupuri indice 2, [(5,3)⁺,2] and [5,3,2]⁺, dar al doilea nu produce 4-politopuri uniforme.

Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție				Numărul elementelor				Desfășurată
Nr.	Nume	Diagramă Schlegel	Figura vârfului	Diagramă Coxeter și simbol Schläfli	Numărul celulelor din poziție				Celule	Fețe	Laturi	Vârfuri	Desfășurată
57	Prismă dodecaedrică			{5,3}×{ } t_0,3{5,3,2}	2 5.5.5	12 4.4.5			14	30 {4} 24 {5}	80	40
58	Prismă icosidodecaedrică		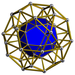	r{5,3}×{ } t_1,3{5,3,2}	2 3.5.3.5	20 3.4.4	12 4.4.5		34	40 {3} 60 {4} 24 {5}	150	60
59	Prismă icosaedrică (același cu prismă tetraedrică snub)			{3,5}×{ } t_2,3{5,3,2}	2 3.3.3.3.3	20 3.4.4			22	40 {3} 30 {4}	72	24
60	Prismă dodecaedrică trunchiată		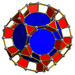	t{5,3}×{ } t_0,1,3{5,3,2}	2 3.10.10	20 3.4.4	12 4.4.10		34	40 {3} 90 {4} 24 {10}	240	120
61	Prismă rombicosidodecaedrică			rr{5,3}×{ } t_0,2,3{5,3,2}	2 3.4.5.4	20 3.4.4	30 4.4.4	12 4.4.5	64	40 {3} 180 {4} 24 {5}	300	120
62	Prismă icosaedrică trunchiată			t{3,5}×{ } t_1,2,3{5,3,2}	2 5.6.6	12 4.4.5	20 4.4.6		34	90 {4} 24 {5} 40 {6}	240	120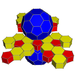
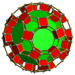
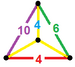
63	Prismă icosidodecaedrică trunchiată			tr{5,3}×{ } t_0,1,2,3{5,3,2}	2 4.6.10	30 4.4.4	20 4.4.6	12 4.4.10	64	240 {4} 40 {6} 24 {10}	480	240
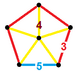
64	Prismă dodecaedrică snub			sr{5,3}×{ }	2 3.3.3.3.5	80 3.4.4	12 4.4.5		94	160 {3} 150 {4} 24 {5}	360	120
Neuniform	Antiprismă dodecahedrică omnisnub			$s\left\{{\begin{array}{l}5\\3\\2\end{array}}\right\}$	2 3.3.3.3.5	30+120 3.3.3	20 3.3.3.3	12 3.3.3.5	184	20+240 {3} 24 {5}	220	120

Duoprisme: [p] × [q][modificare | modificare sursă]

Cea de a doua este familia infinită de duoprisme uniforme, produsul de două poligoane regulate. Diagrama Coxeter–Dynkin a unei duoprisme este . Figura vârfurilor lor este un bisfenoid tetragonal, .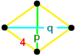

Când unul dintre cele două poligoane „factor” este un pătrat, această familie se suprapune cu prima: produsul este echivalent cu o hiperprismă a cărui bază este o prismă tridimensională. Ordinul de simetrie al unei duoprisme ai cărei factori sunt un p-gon și un q-gon (o duoprismă „p,q”) este de 4pq dacă p ≠ q; dacă factorii sunt ambii p-goane, ordinul de simetrie este 8p². Teseractul poate fi considerat o 4,4-duoprismă.

Elementele unei p,q-duoprisme (p ≥ 3, q ≥ 3) sunt:

celulele: prisme p q-gonale, prisme, q p-gonale;
fețele: pătrate pq, p q-goane, q p-goane;
laturile: 2pq;
vârfurile: pq.

Nu există un analog uniform cvadridimensional cu familia infinită a antiprismelor tridimensionale.

Mulțimea infinită de duoprisme p-q — — prisme p q-gonale, prisme q p-gonale:

Nume	Diagramă Coxeter	Celule	Diagrame Schlegel	Desfășurtă
3-3 duoprismă		3+3 prisme triunghiulare
3-4 duoprismă		3 cubes 4 prisme triunghiulare
4-4 duoprismă (același cu tesseract)		4+4 cuburi
3-5 duoprismă		3 prisme pentagonale 5 prisme triunghiulare
4-5 duoprismă		4 prisme pentagonale 5 cuburi
5-5 duoprismă		5+5 prisme pentagonale
3-6 duoprismă		3 prisme hexagonale 6 prisme triunghiulare
4-6 duoprismă		4 prisme hexagonale 6 cuburi
5-6 duoprismă		5 prisme hexagonale 6 prisme pentagonale
6-6 duoprismă		6+6 prisme hexagonale

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Prisme prismatice poligonale [p] × [ ] × [ ][modificare | modificare sursă]

Mulțimea infinită de prisme prismatice uniforme se suprapune cu duoprismele 4-p: (p ≥ 3) — — p cuburi și 4 prisme p-gonale (toate sunt identice cu duoprisma 4-p ). Al doilea politop din serie este o simetrie inferioară a tesseractului, {4}×{4}.

Prisme prismatice p-gonale convexe^[16]
Nume	{3}×{4}	{4}×{4}	{5}×{4}	{6}×{4}	{7}×{4}	{8}×{4}	{p}×{4}
Diagramă Coxeter
Diagramă Schlegel
Celule	3 {4}×{} 4 {3}×{}	4 {4}×{} 4 {4}×{}	5 {4}×{} 4 {5}×{}	6 {4}×{} 4 {6}×{}	7 {4}×{} 4 {7}×{}	8 {4}×{} 4 {8}×{}	p {4}×{} 4 {p}×{}
Desfășurată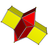

Prisme antiprismatice poligonale: [p] × [ ] × [ ][modificare | modificare sursă]

Mulțimile infinite de prisme antiprismatice uniforme sunt formate din două antiprisme paralele: (p ≥ 2) — — antiprisme 2p-gonale, conectate prin prisme 2p-gonale și 2p prisme triunghiulare.

Prisme antiprismatice p-gonale convexe
Nume	s{2,2}×{}	s{2,3}×{}	{2,4}×{}	s{2,5}×{}	s{2,6}×{}	s{2,7}×{}	s{2,8}×{}	s{2,p}×{}
Diagramă Coxeter
Diagramă Schlegel
Figura vârfului
Celule	2 s{2,2} (2) {2}×{}={4} 4 {3}×{}	2 s{2,3} 2 {3}×{} 6 {3}×{}	2 s{2,4} 2 {4}×{} 8 {3}×{}	2 s{2,5} 2 {5}×{} 10 {3}×{}	2 s{2,6} 2 {6}×{} 12 {3}×{}	2 s{2,7} 2 {7}×{} 14 {3}×{}	2 s{2,8} 2 {8}×{} 16 {3}×{}	2 s{2,p} 2 {p}×{} 2p {3}×{}
Desfășurată

O "prismă antiprismatică p-gonală" are "4p" triunghiuri, "4p" pătrate și 4 fețe p-gonale. Are 10p laturi și 4p vârfuri.

Alternări neuniforme[modificare | modificare sursă]

Coxeter a prezentat doar două soluții uniforme pentru grupurile Coxeter de rangul 4 cu toate inelele alternate (nodurile notate cu cercuri goale). Prima este , s{2^1,1,1} care reprezintă un subgrup indice 24 (simetie [2,2,2]⁺, ordin 8) de forma unui semitesseract, , h{4,3,3} (simetrie [1⁺,4,3,3] = [3^1,1,1], ordin 192). A doua este , s{3^1,1,1}, care este un subgrup indice 6 (simetrie [3^1,1,1]⁺, ordin 96) de forma unui 24-celule snub, , s{3,4,3}, (simetrie [3⁺,4,3], ordin 576).

Alte alternări, ca , o alternare a unui tesseract omnitrunchiat , nu poate fi făcut unifom prin rezolvarea problemei laturilor egale deoarece în general sistemul care-l caracterizează este supradeterminat^⁠(d), având 6 ecuații și doar 4 variabile. Astfel de figuri alternate neuniforme pot fi construite ca 4-politopuri izogonale prin îndepărtarea uneia dintre cele două jumătăți de vârfuri ale figurii complet inelate, dar vor avea lungimi ale laturilor inegale. La fel ca alternările uniforme, vor avea jumătate din simetria figurii uniforme, cum ar fi [4,3,3]⁺, ordin 192, care este simetria tesseractului omnitrunchiat alternat.^[17]

Construcțiile Wythoff cu alternanțe produc figuri izogonale care pot fi făcute echilaterale, dar nu și uniforme, deoarece golurile alternate (în jurul vârfurilor eliminate) creează celule care nu sunt regulate sau semiregulate. Un nume propus pentru astfel de figuri este politopuri scaliforme.^[18] Această categorie admite ca celule un subset de poliedre Johnson, de exemplu cupola triunghiulară.

Fiecare configurație a vârfului dintr-un poliedru Johnson trebuie să existe în figura vârfului. De exemplu, o piramidă pătrată are două configurații ale vârfurilor: 3.3.4 în jurul bazei și 3.3.3.3 la apex.

Desfășuratele și figurile vârfurilor celor două cazuri convexe sunt date mai jos, împreună cu o listă de celule din jurul fiecărui vârf.

Două 4-politopuri convexe izogonale cu celule neuniforme
Diagramă Coxeter	s₃{2,4,3},	s₃{3,4,3},
Relații	24 din 48 de vârfuri ale prismei rombicuboctaedrice	288 din 576 de vârfuri ale 24-celule runcitrunchiat
Desfășurată	4-hosoedru cubic runcic^[19]^[20]	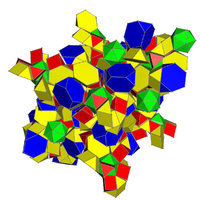24-celule snub runcic^[21]^[22]
Celule
Figura vârfului	(1) 3.4.3.4: cupolă triunghiulară (2) 3.4.6: cupolă triunghiulară (1) 3.3.3: tetraedru (1) 3.6.6: tetraedru trunchiat	(1) 3.4.3.4: cupolă triunghiulară (2) 3.4.6: cupolă triunghiulară (2) 3.4.4: prismă triunghiulară (1) 3.6.6: tetraedru trunchiat (1) 3.3.3.3.3: icosaedru

Derivări geometrice ale celor 46 de 4-politopuri uniforme wythoffiene neprismatice[modificare | modificare sursă]

Cele 46 de politopuri wythoffiene includ cele șase 4-politopuri regulate convexe. Celelalte patruzeci pot fi obținute din 4-politopurile regulate prin operații geometrice care conservă majoritatea sau toate simetriile, prin urmare pot fi clasificate după grupul de simetrie comun.

Diagrama rezumativă a operațiilor de trunchiere	Exemple de poziții ale punctului generator caleidoscopic din domeniul fundamental

Operațiile geometrice prin care se obțin cele 40 de politopuri uniforme din 4-politopurile regulate sunt operații de trunchiere. Un 4-politop poate fi trunchiat la vârfuri, laturi sau fețe, ducând la adăugarea de celule corespunzătoare acelor elemente, fapt prezentat în coloanele tabelelor următoare.

Diagrama Coxeter–Dynkin arată prin noduri cele patru oglinzi ale caleidoscopului wythoffian, iar laturile dintre noduri sunt etichetate cu un număr întreg care arată unghiul dintre oglinzi ( $\pi ,/n$ radiani sau $180^{\circ }/n$ . Nodurile inelate arată care oglinzi sunt active pentru fiecare formă; o oglindă este activă față de un vârf care nu se află pe ea.

Operația	Simbol Schläfli	Simetrie	Descriere
Inițial	t₀{p,q,r}	[p,q,r]	Forma regulată inițială {p,q,r}
Rectificare	t₁{p,q,r}		Trunchierea este aplicată până când laturile inițiale degenerează în puncte.
Birectificare (Dual rectificat)	t₂{p,q,r}		Fețele sunt trunchiate la puncte. Aceeași ca dual rectificat.
Trirectificare (dual)	t₃{p,q,r}		Celulele sunt trunchiate la puncte. Dual regulat {r,q,p}
Trunchiere	t_0,1{p,q,r}		Fiecare vârf este tăiat până la mijlocul fiecărei laturi inițiale. Unde s-a aflat vârful apare o nouă celulă, figura vârfului 4-politopului inițial. Fiecare celulă inițială este, de asemenea, trunchiată.
Bitrunchiere	t_1,2{p,q,r}		O trunchiere între o formă rectificată și forma rectificată duală.
Tritrunchiere	t_2,3{p,q,r}		Dual trunchiat {r,q,p}.
Cantelare	t_0,2{p,q,r}		O trunchiere aplicată laturilor și vârfurilor și definește o progresie între forma regulată rectificată și forma duală rectificată.
Bicantelare	t_1,3{p,q,r}		Dual cantelat {r,q,p}.
Runcinare (sau expandare)	t_0,3{p,q,r}		O trunchiere aplicată celulelor, fețelor și laturilor; definește o progresie între o formă regulată și cea duală.
Cantitrunchiere	t_0,1,2{p,q,r}		Ambele operații de cantelare și trunchiere.
Bicantitrunchiere	t_1,2,3{p,q,r}		Dual cantitrunchiat {r,q,p}.
Runcitrunchiere	t_0,1,3{p,q,r}		Ambele operații de runcinare și trunchiere.
Runcicantelare	t_0,1,3{p,q,r}		Dual runcitrunchiat {r,q,p}.
Omnitrunchiere (runcicantitrunchiere)	t_0,1,2,3{p,q,r}		Toate trei operațiile de cantelare, runcinare și trunchiere.
Înjumătățire	h{2p,3,q}	[1⁺,2p,3,q] =[(3,p,3),q]	Alternare a , aceeași cu
Cantic	h₂{2p,3,q}		Aceeași cu
Runcic	h₃{2p,3,q}		Aceeași cu
Runcicantic	h_2,3{2p,3,q}		Aceeași cu
Sfertuire	q{2p,3,2q}	[1⁺,2p,3,2q,1⁺]	Aceeași cu
Snub	s{p,2q,r}	[p⁺,2q,r]	Trunchiere alternată
Snub cantic	s₂{p,2q,r}		Trunchiere alternată cantelată
Snub runcic	s₃{p,2q,r}		Trunchiere alternată runcinată
Snub runcicantic	s_2,3{p,2q,r}		Trunchiere alternată runcicantelată
Snub rectificat	sr{p,q,2r}	[(p,q)⁺,2r]	Trunchiere alternată rectificată
	ht_0,3{2p,q,2r}	[(2p,q,2r,2⁺)]	Runcinare alternată
Bisnub	2s{2p,q,2r}	[2p,q⁺,2r]	Bitrunchiere alternată
Omnisnub	ht_0,1,2,3{p,q,r}	[p,q,r]⁺	Omnitrunchiere alternată

Dacă două politopuri sunt duale (de exemplu tesseractul și 16-celule, sau 120-celule și 600-celule), atunci „bitrunchierea”, „runcinarea” sau omnitrunchierea produc aceeași figură ca aceeași operație aplicată celuilalt. Astfel, acolo unde în tabel apare doar unul dintre cazuri, trebuie înțeles că se aplică oricăruia dintre cele două 4-politopuri inițiale.

Rezumatul construcțiilor prin simetrie extinsă[modificare | modificare sursă]

Cele 46 de 4-politopuri uniforme construite din simetriile A₄, B₄, F₄ și H₄ sunt date în acest tabel prin simetria lor extinsă completă și diagramele Coxeter. Alternările sunt grupate după simetria lor chirală. Toate alternările sunt date, deși 24-celule snub, cu 3 familii de construcții, este singurul care este uniform. Numerele din paranteză sunt fie repetări, fie neuniforme. Diagramele Coxeter sunt date cu indici 1 până la 46. Sunt incluse familiile duoprismatice 3-3 și 4-4, a doua pentru relația sa cu familia B₄.

Grup Coxeter	Simetrie extinsă	4-politopuri		Simetrie extinsă chirală	Faguri alternați
[3,3,3]	[3,3,3] (order 120)	6	₍₁₎ \| ₍₂₎ \| ₍₃₎ ₍₄₎ \| ₍₇₎ \| ₍₈₎
[3,3,3]	[2⁺[3,3,3]] (order 240)	3	₍₅₎\| ₍₆₎ \| ₍₉₎	[2⁺[3,3,3]]⁺ (order 120)	(1)	₍₋₎
[3,3^1,1]	[3,3^1,1] (order 192)	0	(nu există)
	[1[3,3^1,1]]=[4,3,3] = (order 384)	(4)	₍₁₂₎ \| ₍₁₇₎ \| ₍₁₁₎ \| ₍₁₆₎
	[3[3^1,1,1]]=[3,4,3] = (order 1152)	(3)	₍₂₂₎ \| ₍₂₃₎ \| ₍₂₄₎	[3[3,3^1,1]]⁺ =[3,4,3]⁺ (order 576)	(1)	₍₃₁₎ (= ) ₍₋₎
[4,3,3]	[3[1⁺,4,3,3]]=[3,4,3] = (order 1152)	(3)	₍₂₂₎ \| ₍₂₃₎ \| ₍₂₄₎
	[4,3,3] (order 384)	12	₍₁₀₎ \| ₍₁₁₎ \| ₍₁₂₎ \| ₍₁₃₎ \| ₍₁₄₎ ₍₁₅₎ \| ₍₁₆₎ \| ₍₁₇₎ \| ₍₁₈₎ \| ₍₁₉₎ ₍₂₀₎ \| ₍₂₁₎	[1⁺,4,3,3]⁺ (order 96)	(2)	₍₁₂₎ (= ) ₍₃₁₎ ₍₋₎
	[4,3,3] (order 384)	12		[4,3,3]⁺ (order 192)	(1)	₍₋₎
[3,4,3]	[3,4,3] (order 1152)	6	₍₂₂₎ \| ₍₂₃₎ \| ₍₂₄₎ ₍₂₅₎ \| ₍₂₈₎ \| ₍₂₉₎	[2⁺[3⁺,4,3⁺]] (order 576)	1	₍₃₁₎
[3,4,3]	[2⁺[3,4,3]] (order 2304)	3	₍₂₆₎ \| ₍₂₇₎ \| ₍₃₀₎	[2⁺[3,4,3]]⁺ (order 1152)	(1)	₍₋₎
[5,3,3]	[5,3,3] (order 14400)	15	₍₃₂₎ \| ₍₃₃₎ \| ₍₃₄₎ \| ₍₃₅₎ \| ₍₃₆₎ ₍₃₇₎ \| ₍₃₈₎ \| ₍₃₉₎ \| ₍₄₀₎ \| ₍₄₁₎ ₍₄₂₎ \| ₍₄₃₎ \| ₍₄₄₎ \| ₍₄₅₎ \| ₍₄₆₎	[5,3,3]⁺ (order 7200)	(1)	₍₋₎
[3,2,3]	[3,2,3] (order 36)	0	(nu există)	[3,2,3]⁺ (order 18)	0	(nu există)
	[2⁺[3,2,3]] (order 72)	0		[2⁺[3,2,3]]⁺ (order 36)	0	(nu există)
	[[3],2,3]=[6,2,3] = (order 72)	1		[1[3,2,3]]=[[3],2,3]⁺=[6,2,3]⁺ (order 36)	(1)
	[(2⁺,4)[3,2,3]]=[2⁺[6,2,6]] = (order 288)	1		[(2⁺,4)[3,2,3]]⁺=[2⁺[6,2,6]]⁺ (order 144)	(1)
[4,2,4]	[4,2,4] (order 64)	0	(nu există)	[4,2,4]⁺ (order 32)	0	(nu există)
	[2⁺[4,2,4]] (order 128)	0	(nu există)	[2⁺[(4,2⁺,4,2⁺)]] (order 64)	0	(nu există)
	[(3,3)[4,2*,4]]=[4,3,3] = (order 384)	(1)	₍₁₀₎	[(3,3)[4,2*,4]]⁺=[4,3,3]⁺ (order 192)	(1)	₍₁₂₎
	[[4],2,4]=[8,2,4] = (order 128)	(1)		[1[4,2,4]]=[[4],2,4]⁺=[8,2,4]⁺ (order 64)	(1)
	[(2⁺,4)[4,2,4]]=[2⁺[8,2,8]] = (order 512)	(1)		[(2⁺,4)[4,2,4]]⁺=[2⁺[8,2,8]]⁺ (order 256)	(1)

4-politopuri stelate uniforme[modificare | modificare sursă]

În afară de familiile infinite de prisme și antiprisme menționate mai sus, care au infinit de mulți membri neconvecși, au fost descoperite multe 4-politopuri stelate uniforme. Din 1990 până în 2006 Jonathan Bowers și George Olshevsky, împreună cu alți diverși matematicieni, au găsit sute de 4-politopuri stelate uniforme. Numărul lor exact depinde de definiția utilizată: dacă celulele „exotice” (un n-politop este considerat „exotic” de Bowers dacă orice (n–2)-față conține mai mult de două (n–1)-fețe.^[23]) cele coincidente și cele „fisionare” (un n-politop este considerat „fisionar” de Bowers dacă figura vârfului este o figură compusă.^[23]) sunt admise, au fost descoperite 8190 de 4-politopuri uniforme; în caz contrar, numărul scade la 1849. Bowers a sugerat folosirea numelui uniform polychoroid (în română 4-politopic uniform) pentru membrii grupului extins și uniform polychoron (în română 4-politop uniform) pentru membrii celui restrâns.^[8] În special, aceste 1849 au fost adăugate la software Stella4D, unde pot fi vizualizate și manevrate.^[24]

Note[modificare | modificare sursă]

^ de Edmund Hess, Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder, von dr. Edmund Hess. Mit sechzehn lithographierten tafeln., umich.edu, accesat 2021-05-01
^ en Thorold Gosset, On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
^ en „Archived copy” (PDF). Arhivat din original (PDF) la 29 decembrie 2009. Accesat în 13 august 2010.
^ Elte (1912)
^ de Möller, Marco (2004). Vierdimensionale Archimedische Polytope (PDF) (Doctoral thesis). University of Hamburg.
^ Conway (2008)
^ en [1] Convex and Abstract Polytopes workshop (2005), N.Johnson — "Uniform Polychora" abstract
^ ^a ^b en „Uniform Polychora”. www.polytope.net. Accesat în 20 februarie 2020.
^ en „Uniform Polychora”. www.polytope.net. Accesat în 6 iunie 2021.
^ Coxeter, Regular polytopes, 7.7 Schlaefli's criterion eq 7.78, p.135
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Johnson (2015), Chapter 11, section 11.5 Spherical Coxeter groups, 11.5.5 full polychoric groups
^ en Incidence matrix, bendwavy.org, accesat 2021-05-03
^ en Incidence matrix, bendwavy.org, accesat 2021-05-04
^ en Incidence matrix, bendwavy.org, accesat 2021-05-05
^ en Incidence matrix], bendwavy.org, accesat 2021-05-05
^ Conway (2008), cap. 26
^ en H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, Math. Zeit. 188 (1985) p. 582-588 2.7 The four-dimensional analogues of the snub cube
^ en Politop scaliform, bendwavy.org, accesat 2021-05-07
^ en invtut, bendwavy.org, accesat 2021-05-07
^ en Category S1: Simple Scaliforms: tutcup, polytope.net, accesat 2021-05-07
^ en prissi, bendwavy.org, accesat 2021-05-07
^ en Category S3: Special Scaliforms: prissi, polytope.net, accesat 2021-05-07
^ ^a ^b en Glossary, polytope.net, accesat 2021-05-08
^ en Webb, Robert. „Stella: Polyhedron Navigator”.

Bibliografie[modificare | modificare sursă]

en A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
en B. Grünbaum Convex Polytopes, New York ; London : Springer, c2003. ISBN: 0-387-00424-6.
Second edition prepared by Volker Kaibel, Victor Klee, and Günter M. Ziegler.
en Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen, ISBN 1-4181-7968-X [2] [3]
H.S.M. Coxeter:

H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londen, 1954
H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973

en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6

(Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
(Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

en H.S.M. Coxeter and W. O. J. Moser. Generators and Relations for Discrete Groups 4th ed, Springer-Verlag. New York. 1980 p. 92, p. 122.
en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26)
en John H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
en N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
en N.W. Johnson: Geometries and Transformations, (2015) Chapter 11: Finite symmetry groups
en Richard Klitzing, Snubs, alternated facetings, and Stott-Coxeter-Dynkin diagrams, Symmetry: Culture and Science, Vol. 21, No.4, 329-344, (2010) [4]
en Schoute, Pieter Hendrik (1911), „Analytic treatment of the polytopes regularly derived from the regular polytopes”, Verhandelingen der Koninklijke Akademie van Wetenschappen Te Amsterdam, 11 (3): 87 pp Googlebook, 370-381

Legături externe[modificare | modificare sursă]

4-politopuri uniforme convexe

de Uniform, convex polytopes in four dimensions, Marco Möller
en George Olshevsky, Uniform Polytopes in Four Dimensions

George Olshevsky, Convex uniform polychora based on the pentachoron
George Olshevsky, Convex uniform polychora based on the tesseract/16-cell
George Olshevsky, Convex uniform polychora based on the 24-cell
George Olshevsky, Convex uniform polychora based on the 120-cell/600-cell
George Olshevsky, Anomalous convex uniform polychoron: (grand antiprism)
George Olshevsky, Convex uniform prismatic polychora
George Olshevsky, Uniform polychora derived from glomeric tetrahedron B4

4-politopuri uniforme neconvexe

en Uniform polychora by Jonathan Bowers
en Stella4D Stella (software) produces interactive views of known uniform polychora including the 64 convex forms and the infinite prismatic families.

Alte materiale

en Klitzing, Richard. „4D uniform polytopes”.
en 4D-Polytopes and Their Dual Polytopes of the Coxeter Group W(A4) Represented by Quaternions International Journal of Geometric Methods in Modern Physics,Vol. 9, No. 4 (2012) Mehmet Koca, Nazife Ozdes Koca, Mudhahir Al-Ajmi (2012) [5]

Portal Matematică

v • d • m Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10
Familie	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Poligoane regulate	Triunghi	Pătrat	p-gon	Hexagon	Pentagon
Poliedre uniforme	Tetraedru	Octaedru • Cub	Semicub		Dodecaedru • Icosaedru
4-politopuri uniforme	5-celule	16-celule • Tesseract	Semitesseract	24-celule	120-celule • 600-celule
5-politopuri uniforme	5-simplex	5-ortoplex • 5-cub	5-semicub
6-politopuri uniforme	6-simplex	6-ortoplex • 6-cub	6-semicub	1₂₂ • 2₂₁
7-politopuri uniforme	7-simplex	7-ortoplex • 7-cub	7-semicub	1₃₂ • 2₃₁ • 3₂₁
8-politopuri uniforme	8-simplex	8-ortoplex • 8-cub	8-semicub	1₄₂ • 2₄₁ • 4₂₁
9-politopuri uniforme	9-simplex	9-ortoplex • 9-cub	9-semicub
10-politopuri uniforme	10-simplex	10-ortoplex • 10-cub	10-semicub
n-politopuri uniforme	n-simplex	n-ortoplex • n-cub	n-semicub	1_k2 • 2_k1 • k₂₁	n-politop pentagonal
Topicuri: Familii de politopuri • Politop regulat

[1] Edmund Hess, Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder, von dr. Edmund Hess. Mit sechzehn lithographierten tafeln., umich.edu, accesat 2021-05-01

[2] Thorold Gosset, On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900

[3] „Archived copy” (PDF). Arhivat din original (PDF) la 29 decembrie 2009. Accesat în 13 august 2010.

[4] Elte (1912)

[5] Möller, Marco (2004). Vierdimensionale Archimedische Polytope (PDF) (Doctoral thesis). University of Hamburg.

[6] Conway (2008)

[7] [1] Convex and Abstract Polytopes workshop (2005), N.Johnson — "Uniform Polychora" abstract

[BO-8] „Uniform Polychora”. www.polytope.net. Accesat în 20 februarie 2020.

[9] „Uniform Polychora”. www.polytope.net. Accesat în 6 iunie 2021.

[10] Coxeter, Regular polytopes, 7.7 Schlaefli's criterion eq 7.78, p.135

[grupuri_4D-11] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Johnson (2015), Chapter 11, section 11.5 Spherical Coxeter groups, 11.5.5 full polychoric groups

[12] Incidence matrix, bendwavy.org, accesat 2021-05-03

[13] Incidence matrix, bendwavy.org, accesat 2021-05-04

[14] Incidence matrix, bendwavy.org, accesat 2021-05-05

[15] Incidence matrix], bendwavy.org, accesat 2021-05-05

[16] Conway (2008), cap. 26

[17] H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, Math. Zeit. 188 (1985) p. 582-588 2.7 The four-dimensional analogues of the snub cube

[18] Politop scaliform, bendwavy.org, accesat 2021-05-07

[19] vtut, bendwavy.org, accesat 2021-05-07

[20] Category S1: Simple Scaliforms: tutcup, polytope.net, accesat 2021-05-07

[21] rissi, bendwavy.org, accesat 2021-05-07

[22] Category S3: Special Scaliforms: prissi, polytope.net, accesat 2021-05-07

[glosar-23] Glossary, polytope.net, accesat 2021-05-08

[24] Webb, Robert. „Stella: Polyhedron Navigator”.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]