120-celule
| 120-celule regulat (dodecaplex) | |
 Diagramă Schlegel (vârfuri și laturi) | |
| Tip | 4-politop regulat convex |
|---|---|
| Simbol Schläfli | {5,3,3} |
| Diagramă Coxeter | |
| Celule | 120 {5,3} |
| Fețe | 720 {5} |
| Laturi | 1200 |
| Vârfuri | 600 |
| Figura vârfului |  Tetraedru |
| Poligon Petrie | 30-gon |
| Grup Coxeter | H4, [3,3,5], ordin 1440 |
| Dual | 600-celule |
| Proprietăți | convex, izogonal, izotoxal, izoedric |
| Index uniform | 32 |

În geometrie 120-celule[a] este un obiect din spațiul cvadridimensional, unul dintre cele șase 4-politopuri convexe regulate descrise pentru prima dată de matematicianul elvețian Ludwig Schläfli la mijlocul secolului al XIX-lea. Mai este cunoscut sub numele de dodecaplex (prescurtare a expresiei „complex de dodecaedre”), hiperdodecaedru sau C120.[1]
Poate fi considerat analogul în 4 dimensiuni al dodecaedrului regulat. Așa cum un dodecaedru poate fi construit din 12 pentagoane, câte 3 în jurul fiecărui vârf, „dodecaplexul” poate fi construit din 120 celule dodecaedrice, care se întâlnesc câte 3 în jurul fiecărei laturi și câte 4 în fiecare vârf.
Elemente[modificare | modificare sursă]
- Are 120 de celule, 720 de fețe pentagonale, 1200 de laturi și 600 de vârfuri.
- La fiecare vârf se întâlnesc câte 4 dodecaedre, 6 pentagoane și 4 laturi.
- La fiecare latură se întâlnesc câte 3 dodecaedre și 3 pentagoane.
- Politopul său dual este 600-celule.
- Împreună cu dualul său formează compusul de 120-celule și 600-celule.
- Figura vârfului 120-celule este un tetraedru.
- Unghiul diedru (între hiperplanele fațetelor este 144°.[2]
Configurație[modificare | modificare sursă]
Matricea de configurație de mai jos descrie 120-celule. Rândurile și coloanele corespund vârfurilor, laturilor, fețelor și celulelor. Numerele de pe diagonale spun câte din fiecare element apar în întreagul 120-celule. Celelalte numere indică câte dintre elementele coloanei apar în sau la elementul rândului.[3][4]
Tabelul următor arată configurația extinsă cu k-elemente de față și k-figuri. Numărul de elemente diagonale reprezintă ordinul întregului grup Coxeter, 14400, împărțit la ordinul subgrupului cu eliminarea oglinzii.
| H4 | k-față | fk | f0 | f1 | f2 | f3 | k-fig | Note | |
|---|---|---|---|---|---|---|---|---|---|
| A3 | ( ) | f0 | 600 | 4 | 6 | 4 | {3,3} | H4/A3 = 14400/24 = 600 | |
| A1A2 | { } | f1 | 2 | 720 | 3 | 3 | {3} | H4/A2A1 = 14400/6/2 = 1200 | |
| H2A1 | {5} | f2 | 5 | 5 | 1200 | 2 | { } | H4/H2A1 = 14400/10/2 = 720 | |
| H3 | {5,3} | f3 | 20 | 30 | 12 | 120 | ( ) | H4/H3 = 14400/120 = 120 |
Coordonate carteziene[modificare | modificare sursă]
Cele 600 de vârfuri ale unui 120-celule cu o lungime a laturii de 2φ2 = 3–√5 și o rază de la centru la vârf de √8 = 2√2 include toate permutările:[5]
- (0, 0, ±2, ±2)
- (±1, ±1, ±1, ±√5)
- (±φ−2, ±φ, ±φ, ±φ)
- (±φ−1, ±φ−1, ±φ−1, ±φ2)
și toate permutările pare ale:
- (0, ±φ−2, ±1, ±φ2)
- (0, ±φ−1, ±φ, ±√5)
- (±φ−1, ±1, ±φ, ±2)
unde φ este secțiunea de aur, 1 + √52.
Având în vedere matricea de adiacență a vârfurilor reprezentând graful său poliedric, diametrul grafului este 15, conectând fiecare vârf cu cel de la negativul coordonatelor sale, la o distanță de 4√2. Există 24 de căi diferite de a le conecta de-a lungul laturilor politopului. Din fiecare vârf există 4 vârfuri la distanța 1, 12 la distanța 2, 24 la distanța 3, 36 la distanța 4, 52 la distanța 5, 68 la distanța 6, 76 la distanța 7, 78 la distanța 8, 72 la distanță 9, 64 la distanță 10, 56 la distanță 11, 40 la distanță 12, 12 la distanță 13, 4 la distanță 14 și 1 la distanță 15. Matricea de adiacență are 27 de valori proprii distincte variind de la 2φ2, cu o multiplicitate de 4, la 4, cu o multiplicitate de 1. Multiplicitatea valorii proprii 0 este 18, iar rangul matricei de adiacență este 582.
Vizualizare[modificare | modificare sursă]
120-celule este format din 120 de celule dodecaedrice. În scopul vizualizării este convenabil ca dodecaedrele să fie aliniate (o trăsătură pe care o au și celulele tesseractului și 24-celulei). Se pot alinia dodecaedrele față la față pe o dreaptă îndoită în a 4-a dimensiune într-un cerc mare cu o circumferință de 10 celule. Pornind de la această construcție inițială de zece celule, există două vizualizări obișnuite care pot fi folosite: o proiecție stereografică stratificată și o structură de inele care se împletesc.
Proiecția stereografică stratificată[modificare | modificare sursă]
Pozițiile celulelor se pretează la o descriere hipersferică. Fie un dodecaedru arbitrar etichetat „polul nord”. Douăsprezece arce de cercuri mari meridiane (lungi de patru celule) sunt distribuite radial în 3 dimensiuni, convergând într-o a cincea celulă, „polul sud”. Acest schelet reprezintă 50 din cele 120 de celule (2 + 4 × 12).
Începând de la polul nord, în tabelul de mai jos se construiește 120-celule în 9 straturi pe latitudine, în stilul topografiei terestre a 2-sferei. Cu excepția polilor, centroizii celulelor fiecărui strat se află pe o 2-sferă separată, cu centroizii ecuatoriali care se află pe o mare 2-sferă. Centroizii celor 30 de celule ecuatoriale formează vârfurile unui icosidodecaedru, cu meridianele (așa cum s-a descris mai sus) trecând prin centrul fiecărei fețe pentagonale. Celulele etichetate „interstițiale” în tabelul următor nu sunt pe cercurile mari meridiane.
| Nr. strat | Nr. celule | Descriere | Colatitudine | Regiune |
|---|---|---|---|---|
| 1 | 1 | Polul nord | 0° | Emisfera nordică |
| 2 | 12 | Primul strat al celulelor meridionale / "Cercul Arctic" | 36° | |
| 3 | 20 | Nemeridian / interstițial | 60° | |
| 4 | 12 | Al doilea strat al celulelor meridionale / "Tropicul Cancerului" | 72° | |
| 5 | 30 | Nemeridian / interstițial | 90° | Ecuator |
| 6 | 12 | Al treilea strat al celulelor meridionale / "Tropicul Capricornului" | 108° | Emisfera sudică |
| 7 | 20 | Nemeridian / interstițial | 120° | |
| 8 | 12 | Al patrulea strat al celulelor meridionale / "Cercul Antarctic" | 144° | |
| 9 | 1 | Polul sud | 180° | |
| Total | 120 celule | |||
Celulele straturilor 2, 4, 6 și 8 sunt situate peste fețele celulelor polare. Celulele straturilor 3 și 7 sunt situate direct pe vârfurile celulelor polare. Celulele stratului 5 sunt situate pe laturile celulelor polare.
Structura de inele care se împletesc[modificare | modificare sursă]


120-celule poate fi divizat în 12 inele de cercuri mari de câte 10 celule, disjuncte, formând o fibrare Hopf discretă/cuantificată. Începând cu un inel cu 10 celule, se poate așeza un alt inel alături de el, care spiralează în jurul primului inel, executând o revoluție completă la 10 celule. Cinci astfel de inele cu 10 celule pot fi plasate adiacent inelului inițial. Deși inelele exterioare „spiralează” în jurul inelului interior (și fiecare în jurul fiecăruia), ele nu au de fapt o formă elicoidală torsionată. Toate sunt echivalente. Spiralarea este rezultatul curburii 3-sferei. Inelul „interior” și cele cinci inele „exterioare” formează acum un tor cu șase inele și 60 de celule. Se poate continua adăugarea de inele cu 10 celule adiacente celor anterioare, dar este mai instructivă construcția unui al doilea tor, disjunct de cel de mai sus, din celelalte 60 de celule, care se interconectează cu primul. 120-celule, ca și 3-sfera, este reuniunea acestor două toruri (Clifford). Dacă inelul central al primului tor este un cerc mare meridian așa cum s-a definit mai sus, inelul central al celui de-al doilea tor este cercul mare ecuatorial care este centrat pe cercul meridian. De reținut că învelișul spiralat de 50 de celule în jurul unui inel central poate fi pe stânga sau pe drepta. Este doar o chestiune de divizare diferită a celulelor, adică de alegerea unui alt set de cercuri mari disjuncte.
Alte construcții ale cercului mare[modificare | modificare sursă]
Există o altă cale a cercurilor mari care prezintă interes, cea care trece alternativ prin vârfurile celulelor opuse, apoi de-a lungul unei laturi. Această cale este formată din 6 celule și 6 margini. Ambele căi ale cercurilor mari de mai sus au căi duale ale cercurilor mari în 600-celule. Calea precedentă de 10 celule față la față se aplică pe calea celor 10 vârfuri care trece de-a lungul laturilor 600-celulei, formând un decagon. Calea alternată celulă/latură de mai sus se aplică pe o cale constând din 12 tetraedre care se întâlnesc alternat față la față, apoi vârf la vârf (șase bipiramide triunghiulare) în 600-celule. Această din urmă cale corespunde unui inel format din șase icosaedre care se întâlnesc față la față în 24-celule snub (sau piramidă icosaedrică în 600-celule).
Proiecții[modificare | modificare sursă]
Proiecții ortogonale[modificare | modificare sursă]
Proiecția ortogonală a unui 120-celule se poate face în 2D prin definirea a doi vectori de bază ortonormali pentru o direcție specifică de vizualizare. Proiecția 30-gonală a fost realizată în 1963 de B.L. Chilton.[6]
Proiecția H3 decagonală arată planul poligonului van Oss.
| H4 | – | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] |
 [6] |
 [4] |
Proiecțiile ortogonale tridimensionale pot fi realizate cu trei vectori de bază ortonormali și afișate ca model 3D, apoi proiectând o anumită perspectivă tridimensională într-o imagine 2D.
 Proiecție izometrică 3D |
Rotație cvadridimensională animată |
Proiecții în perspectivă[modificare | modificare sursă]
Acestea sunt proiecții în perspectivă, dintr-un punct de vedere din spațiul cvadridimensional, și proiectează modelul ca o imagine 3D. Prin urmare, fețele și celulele care par mai mari sunt doar mai aproape de punctul de vedere 4D. Diagrama Schlegel folosește perspectiva pentru a afișa figuri cvadridimensionale, alegând un punct deasupra unei anumite celule, făcând astfel celula să fie anvelopa 3D, iar alte celule sunt văzute mai mici în interiorul ei. Proiecția stereografică utilizează aceeași abordare, dar sunt prezentate cu laturile curbate, reprezentând politopul ca o teselare a unei 3-sfere.
În tabelul următor se prezintă o comparație a proiecțiilor în perspectivă ale unui dodecaedru (tridimensional) și a unui 120-celule (cvadridimensional).
| Proiecție | Dodecaedru | 120-celule |
|---|---|---|
| Diagramă Schlegel |  12 fețe pentagonale bidimensionale |
 120 de celule dodecaedrice tridimensionale |
| Proiecție stereografică | 
|
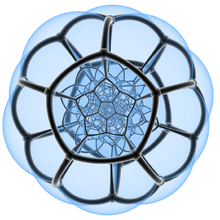 Cu fețe transparente |

|
Proiecție în perspectivă cu o celulă în față, de la de 5 ori distanța de la punctul de vedere la un vârf, cu aceste modificări:
|

|
Proiecție în perspectivă cu un vârf în față, de la de 5 ori distanța de la punctul de vedere la un vârf, cu aceste modificări:
|
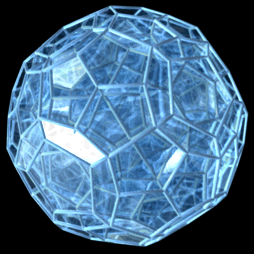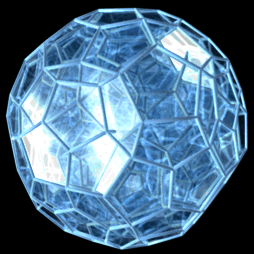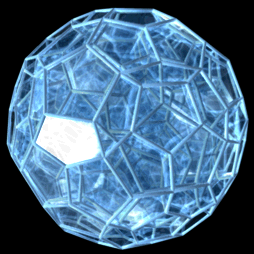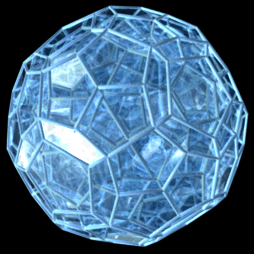
|
O proiecție 3D a unui 120-celule care efectuează o rotație simplă. |

|
O proiecție 3D a unei 120-celule care efectuează o rotație simplă (văzută din interior). |
| Rotație cvadridimensională animată. |
Poliedre și faguri asociați[modificare | modificare sursă]
120-celule este unul dintre cele 15 politopuri regulate și uniforme cu aceeași simetrie [3,3,5]:
| Familia de politopuri H4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 120-celule | 120-celule rectificat |
120-celule trunchiat |
120-celule cantelat |
120-celule runcinat |
120-celule cantitrunchiat |
120-celule runcitrunchiat |
120-celule omnitrunchiat | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||

|

|

|

|

|

|

|

| ||||

|

|

|

|

|

|

| |||||
| 600-celule | 600-celule rectificat |
600-celule trunchiat |
600-celule cantelat |
600-celule bitrunchiat |
600-celule cantitrunchiat | 600-celule runcitrunchiat |
600-celule omnitrunchiat | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||
Este similar cu trei 4-politopuri regulate din spațiul cvadridimensional euclidian: 5-celule {3,3,3}, tesseract {4,3,3}, și fagurele pavare hexagonală din spațiul hiperbolic. Toate acestea au tetraedrul ca figura vârfului.
| Politopuri {p,3,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spațiu | S3 | H3 | |||||||||
| Formă | Finit | Paracompact | Necompact | ||||||||
| Nume | {3,3,3} | {4,3,3} | {5,3,3} | {6,3,3} | {7,3,3} | {8,3,3} | ...{∞,3,3} | ||||
| Imagine | 
|

|

|

|

|

|

| ||||
| Celule {p,3} |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞,3} | ||||
Acest fagure face parte dintr-o secvență de 4-politopuri și faguri cu celule dodecaedrice:
| Politopuri {5,3,p} | |||||||
|---|---|---|---|---|---|---|---|
| Spațiu | S3 | H3 | |||||
| Formă | Finit | Compact | Paracompact | Necompact | |||
| Nume | {5,3,3} | {5,3,4} | {5,3,5} | {5,3,6} | {5,3,7} | {5,3,8} | ... {5,3,∞} |
| Imagine | 
|

|

|

|

|
|

|
| Figura vârfului |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} |
Note explicative[modificare | modificare sursă]
- ^ „120-celule” este o prescurtare a expresiei din limba română „un politop cvadridimensional format din 120 de celule”, plural „două sau mai multe politopuri cvadridimesnsionale formate din câte 120 de celule”, expresii care se acordă corespunzător, deci se vorbește despre „un/acel 120-celule”, nu „o/acea 120-celule”, respectiv „unele/acele 120-celule”', nu „unii/acei 120-celule”. La fel la celelalte politopuri ale căror nume este de forma „n-celule”.
Note[modificare | modificare sursă]
- ^ en N.W. Johnson: Geometries and Transformations, (2018) ISBN: 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249
- ^ Coxeter, Regular polytopes, p.293
- ^ Coxeter, Regular Polytopes, sec 1.8 Configurations
- ^ Coxeter, Complex Regular Polytopes, p. 117
- ^ Eric W. Weisstein, 120-cell la MathWorld.
- ^ en B.L. Chilton, "B.+L.+Chilton"+polytopes On the projection of the regular polytope {5,3,3} into a regular triacontagon, Canadian Mathematical Bulletin, 1964, p. 385–398
Bibliografie[modificare | modificare sursă]
- en H.S.M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN: 0-486-61480-8.
- en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, Math. Zeit. 46 (1940) 380-407, MR 2,10
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, Math. Zeit. 188 (1985) 559-591
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, Math. Zeit. 200 (1988) 3-45
- en John Horton Conway, Michael Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- en Davis, Michael W. (), „A hyperbolic 4-manifold”, Proceedings of the American Mathematical Society, 93 (2): 325–328, doi:10.2307/2044771, ISSN 0002-9939, JSTOR 2044771, MR 0770546
- Norman Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- de Four-dimensional Archimedean Polytopes (German), Marco Möller, PhD dissertation Arhivat în , la Wayback Machine., 2004
Legături externe[modificare | modificare sursă]
 Materiale media legate de 120-celule la Wikimedia Commons
Materiale media legate de 120-celule la Wikimedia Commons- en Eric W. Weisstein, 120-Cell la MathWorld.
- en George Olshevsky. „Hecatonicosachoron”. Glossary for Hyperspace. Arhivat din original la .
- en Klitzing, Richard. „4D uniform polytopes (polychora) o3o3o5x - hi”.
- de Der 120-Zeller (120-cell) Marco Möller's Regular polytopes in R4 (German)
- en 120-cell explorer – A free interactive program that allows you to learn about a number of the 120-cell symmetries. The 120-cell is projected to 3 dimensions and then rendered using OpenGL.
- en Construction of the Hyper-Dodecahedron
- en YouTube animation of the construction of the 120-cell Gian Marco Todesco.
| Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familie | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Poligoane regulate | Triunghi | Pătrat | p-gon | Hexagon | Pentagon | |||||||
| Poliedre uniforme | Tetraedru | Octaedru • Cub | Semicub | Dodecaedru • Icosaedru | ||||||||
| 4-politopuri uniforme | 5-celule | 16-celule • Tesseract | Semitesseract | 24-celule | 120-celule • 600-celule | |||||||
| 5-politopuri uniforme | 5-simplex | 5-ortoplex • 5-cub | 5-semicub | |||||||||
| 6-politopuri uniforme | 6-simplex | 6-ortoplex • 6-cub | 6-semicub | 122 • 221 | ||||||||
| 7-politopuri uniforme | 7-simplex | 7-ortoplex • 7-cub | 7-semicub | 132 • 231 • 321 | ||||||||
| 8-politopuri uniforme | 8-simplex | 8-ortoplex • 8-cub | 8-semicub | 142 • 241 • 421 | ||||||||
| 9-politopuri uniforme | 9-simplex | 9-ortoplex • 9-cub | 9-semicub | |||||||||
| 10-politopuri uniforme | 10-simplex | 10-ortoplex • 10-cub | 10-semicub | |||||||||
| n-politopuri uniforme | n-simplex | n-ortoplex • n-cub | n-semicub | 1k2 • 2k1 • k21 | n-politop pentagonal | |||||||
| Topicuri: Familii de politopuri • Politop regulat | ||||||||||||

