Geometrie în spațiu

Hiperboloid cu o pânză

În matematică geometria în spațiu este numele tradițional pentru geometria spațiului euclidian tridimensional.

Stereometria este ramura geometriei în spațiu care se ocupă cu măsurarea volumului corpurilor solide, cum ar fi piramidele și trunchiurile de piramidă, prismele și alte poliedre, cilindrii; conurile și trunchiurile de con, bilele mărginite de sfere etc.

Istoric

Școala pitagoreică s-a ocupat de poliedrele platonice, dar piramida, prisma, conul și cilindrul nu au fost studiate până la platonicieni. Eudoxus din Knidos a stabilit măsurarea acestora, dovedind că piramida și conul au o treime din volumul unei prisme, respectiv a unui cilindru cu aceeași bază și de aceeași înălțime. Probabil că a fost și descoperitorul unei demonstrații că volumul înconjurat de o sferă este proporțional cu cubul razei sale.

Subiecte

Subiecte de bază în geometria în spațiu și stereometrie:

• Chestiuni de situare în plane și drepte
• Unghi diedru și unghi solid
• Cub și paralelipiped
• Tetraedru și alte piramide
• Prisme
• Octaedru, dodecaedru, icosaedru
• Cilindru și con
• Sferă
• Cuadrice: elipsoid, paraboloid și hiperboloid.

Subiecte avansate:

• Geometrie proiectivă tridimensională (conducând la demonstrarea teoremei lui Desargues folosind o dimensiune suplimentară)
• Geometrie descriptivă
• Alte poliedre.

Corpuri în spațiu

O sferă este suprafața unei bile, dar uneori este ambiguu dacă termenul se referă la suprafața figurii sau la volumul inclus în aceasta, la fel și la cilindru. Următorul tabel cuprinde tipuri majore de forme care fie constituie, fie definesc un volum.

Figură	Definiții	Imagini
Paralelipiped	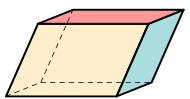Un poliedru cu șase fețe în formă de paralelogram Un hexaedru cu trei perechi de fețe paralele O prismă a cărei bază este un paralelogram
Romboedru	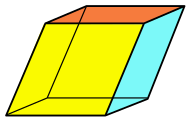Un paralelipiped cu toate laturile de aceeași lungime Un paralelipiped cu fețe rombice
Paralelipiped dreptunghic	Un poliedru convex cu fețe dreptunghiulare, ale cărui graf poliedric este la fel cu al cubului
Poliedru	Cu fețe poligonale, laturi drepte și vârfuri ascuțite	Micul dodecaedru stelat Poliedru toroidal
Poliedru uniform	Cu fețe poligoane regulate și tranzitiv pe vârfuri	Tetraedru Dodecaedru snub
Prismă	Un poliedru cu baza un poligon cu n laturi, o a doua bază obținută prin translația fără rotație a primei baze și n fețe laterale, obligatoriu paralelograme, care unesc laturile corespondente ale bazelor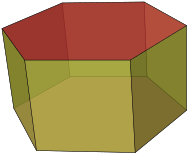
Con	Figură care se îngustează de la o bază plată (frecvent, deși nu neapărat, circulară) până la un punct numit vârf sau apex	Con circular drept și oblic
Cilindru	Suprafață laterală formată din drepte paralele și o secțiune transversală generată de o curbă închisă (de obicei un cerc sau o elipsă)	Cilindru eliptic Cilindri circulari, drept și oblic
Elipsoid	O suprafață care poate fi obținută dintr-o sferă prin scalare direcțională, sau, mai general printr-o transformare afină⁠(d)	Exemple de elipsoizi cu ecuația ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1$ sferă (sus, a=b=c=4), sferoid (jos stânga, a=b=5, c=3), elipsoid (jos dreapta, a=4.5, b=6, c=3)
Hiperboloid	Suprafață generată prin rotația unei hiperbole în jurul unei axe a sa

Tehnici

În geometria în spațiu sunt utilizate diverse tehnici și instrumente. Printre acestea, tehnicile geometria analitică și vectorii euclidieni au un impact major, permițând utilizarea sistematică a sistemelor de ecuații liniare și a algebrei matriciale, care sunt importante pentru dimensiuni superioare.

Bibliografie

• en Kiselev, A. P. (2008). Geometry. Book II. Stereometry. Tradus de Givental, Alexander. Sumizdat.