Mecanică clasică

Diagrama mișcării orbitale a unui satelit în jurul Pământului, care prezintă vectori perpendiculari cu viteza și accelerația (forță).

Mecanica clasică descrie mișcarea obiectelor macroscopice, de la proiectile la părți de mașinării și obiecte astronomice precum nave spațiale, planete, stele și galaxii.

Dacă starea actuală a unui obiect este cunoscută, este posibil să prezicem prin legile mecanicii clasice cum se va mișca în viitor (determinism) și cum s-a mișcat în trecut (reversibilitate).

Cea mai timpurie dezvoltare a mecanicii clasice este adesea denumită mecanică newtoniană. Este formată din conceptele fizice folosite și metodele matematice inventate de Isaac Newton, Gottfried Wilhelm Leibniz și alții în secolul al XVII-lea pentru a descrie mișcarea corpurilor sub influența unui sistem de forțe.

Ulterior, au fost dezvoltate metode mai abstracte, ceea ce a dus la reformularea mecanicii clasice cunoscute sub numele de mecanica lagrangiană și mecanica hamiltoniană. Aceste progrese, realizate cu precădere în secolele al XVIII-lea și al XIX-lea, se extind substanțial dincolo de activitatea lui Newton, în special prin utilizarea lor de mecanica analitică. Acestea sunt utilizate, cu unele modificări, în toate domeniile fizicii moderne.

Mecanica clasică oferă rezultate extrem de precise atunci când sunt studiate obiecte mari care nu sunt extrem de masive și viteze care nu se apropie de viteza luminii. Atunci când obiectele examinate au aproximativ dimensiunea unui diametru de atom, devine necesară introducerea celuilalt subdomeniu major al mecanicii: mecanica cuantică. Pentru a descrie viteze care nu sunt mici în raport cu viteza luminii, este nevoie de relativitatea restrânsă. În cazul în care obiectele devin extrem de masive, se aplică relativitatea generală. Totuși, o serie de surse moderne includ mecanica relativistă în fizica clasică, care în opinia lor reprezintă mecanica clasică în forma ei cea mai dezvoltată și precisă.

Descrierea teoriei

Analiza mișcării proiectilelor este o parte a mecanicii clasice.

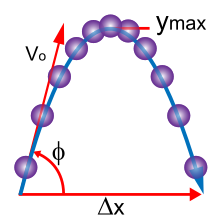
Următorul text introduce conceptele de bază ale mecanicii clasice. Pentru simplitate, modelează adesea obiectele din lumea reală sub formă de particule punctiforme (obiecte cu dimensiuni neglijabile). Mișcarea unei particule punctiforme este caracterizată de un număr mic de parametri: poziție, masă și forțele aplicate acesteia. Fiecare dintre acești parametri este discutat pe rând.

În realitate, genul de obiecte pe care le poate descrie mecanica clasică au întotdeauna o mărime diferită de zero. (Fizica particulelor foarte mici, cum ar fi electronul, este descrisă mai precis de mecanica cuantică). Obiectele cu mărimea non-zero au un comportament mai complicat decât particulele punctiforme ipotetice, din cauza gradelor suplimentare de libertate. Rezultatele particulelor punctiforme pot fi utilizate pentru a studia astfel de obiecte tratându-le ca obiecte compuse, făcute dintr-un număr mare de particule punctiforme cu acțiune colectivă. Centrul de masă al unui obiect compus se comportă ca o particulă punctiformă.

Mecanica clasică folosește noțiuni de bun-simț despre modul în care materia și forțele există și interacționează. Presupune că materia și energia au atribute definite și cunoscute, precum amplasarea în spațiu și viteza. Mecanica non-relativistă presupune, de asemenea, că forțele acționează instantaneu.

Poziția și derivatele sale

Articol principal: Cinematică.

Poziția unei particule punctiforme este definită în raport cu un sistem de coordonate centrat pe un punct de referință fix arbitrar în spațiu numit originea O. Un sistem simplu de coordonate poate descrie poziția unei particule P cu un vector notat de o săgeată etichetată r care arată sensul de la originea O până la punctul P. În general, particula punctiformă nu trebuie să fie staționată în raport cu O. În cazurile în care P se deplasează în raport cu O, r este definit ca funcție a timpului t. În relativitatea pre-Einstein (cunoscută sub numele de relativitate galileeană), timpul este considerat un lucru absolut, adică intervalul de timp între oricare pereche de evenimente, este același pentru toți observatorii. Pe lângă faptul că se bazează pe timpul absolut, mecanica clasică presupune geometria euclidiană pentru structura spațiului.

Viteza vectorială și scalară

Articole principale: Viteză și Viteză liniară.

Cantitățile cinemice ale unei particule clasice: masa m, poziția r, viteza v, accelerația a.

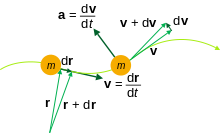
Viteza sau rata de schimbare a poziției în timp, este definită ca derivată a poziției în raport cu timpul:

$\mathbf {v} ={\mathrm {d} \mathbf {r} \over \mathrm {d} t}\,\!$

În mecanica clasică, vitezele sunt direct aditive și substractive. De exemplu, dacă o mașină se deplasează spre est cu 60 km/h și depășește o altă mașină care călătorește în aceeași direcție cu 50 km/h, mașina mai lentă percepe mașina mai rapidă ca deplasându-se spre est cu 60-50 = 10 km/h. Din perspectiva mașinii mai rapide, mașina mai lentă se deplasează cu 10 km/h spre vest, adesea notată ca -10 km/h, unde semnul implică direcție opusă. Vitezele sunt direct aditive sub formă de cantități vectoriale; ele trebuie tratate folosind analiza vectorială.

Accelerație

Articol principal: Accelerație.

Accelerația sau rata de schimbare a vitezei, este derivata vitezei în raport cu timpul (a doua derivată a poziției în raport cu timpul):

$\mathbf {a} ={\mathrm {d} \mathbf {v} \over \mathrm {d} t}={\mathrm {d^{2}} \mathbf {r} \over \mathrm {d} t^{2}}$

Accelerația reprezintă schimbarea vitezei în timp. Viteza poate fi modificată fie în mărime, fie în direcție, sau în ambele. Ocazional, o scădere a mărimii vitezei "v" este denumită decelerație, dar, în general, orice schimbare a vitezei în timp, inclusiv decelerația, este denumită pur și simplu accelerație.

Sistem de referință

Articol principal: Sistem de referință inerțial.

Parte a seriei de articole despre
Mecanică clasică
${\vec {F}}=m{\vec {a}}$ Principiul al II-lea al mecanicii
Istorie Cronologie
Ramuri Cinematică Dinamică Mecanică cerească aplicată a mediilor continue statistică Statică
Concepte Accelerație Energie cinetică potențială de rotație Forță aparentă contact frecare suprafață volum Impuls Inerție Lucru mecanic virtual Masă Moment cinetic de inerție Principiul lui D'Alembert Putere Randament mecanic Sistem de referință inerțial neinerțial Spațiu Timp Viteză relativă
Formulări Legile lui Newton Mecanică analitică Mecanică lagrangiană Mecanică hamiltoniană Ecuația Hamilton–Jacobi
Subiecte de bază Deplasare Legea atracției universale Mișcare ecuații armonică rectilinie Solid rigid
Rotație Rotație Sistem de referință în rotație Viteză unghiulară Accelerație unghiulară Forță centripetă centrifugă Forța Coriolis Frecvență Oscilație oscilator armonic amortizare Pendul conic Vibrație
Oameni de știință Galileo Huygens Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
Categorii Mecanică clasică

În timp ce poziția, viteza și accelerația unei particule pot fi descrise cu privire la orice observator în orice stare de mișcare, mecanica clasică presupune existența unei familii speciale de sisteme de referință în care legile mecanice ale naturii iau o formă relativ simplă. Aceste sisteme speciale de referință se numesc sisteme inerțiale. Un sistem inerțial este un sistem de referință idealizat în cadrul căruia un obiect nu are nici o forță externă care acționează asupra lui. Deoarece nu există nici o forță externă care acționează asupra sa, obiectul are o viteză constantă; adică este în repaus sau se deplasează uniform în linie dreaptă.

Un concept cheie al sistemului inerțial este metoda de identificare a acestora. Pentru scopuri practice, sistemele de referință care nu accelerează în raport cu stelele îndepărtate (un punct extrem de îndepărtat) sunt considerate bune aproximații la sisteme inerțiale. Sistemele de referință non-inerțiale accelerează în raport cu un sistem inerțial existent. Ele constituie baza relativității lui Einstein. Datorită mișcării relative, particulele din cadrul sistemului non-inerțial par să se miște în moduri care nu sunt explicate de forțele din câmpurile existente în sistemul de referință. Prin urmare, se pare că există alte forțe care intră în ecuațiile mișcării numai ca urmare a accelerării relative. Aceste forțe sunt denumite forțe aparente, forțe de inerție sau pseudo-forțe.

Conceptul de forță și a doua lege a lui Newton

Articole principale: Forță și Legile lui Newton.

O forță în fizică este orice acțiune care determină schimbarea vitezei unui obiect. O forță provine din interiorul unui câmp, cum ar fi un câmp electrostatic (cauzat de sarcini electrice statice), câmp electromagnetic (cauzat de sarcini în mișcare) sau câmp gravitațional (cauzat de masă), printre altele.

Newton a fost primul care a exprimat matematic relația dintre forță și impuls. Unii fizicieni interpretează a doua lege a mișcării a lui Newton ca o definiție a forței și a masei, în timp ce alții o consideră un postulat fundamental, o lege a naturii. Fiecare interpretare are aceleași consecințe matematice, cunoscută istoric ca „A doua lege a lui Newton”:

$\mathbf {F} ={\mathrm {d} \mathbf {p} \over \mathrm {d} t}={\mathrm {d} (m\mathbf {v} ) \over \mathrm {d} t}$

unde $\mathbf {p} =m\mathbf {v}$ se numește impuls și este un concept important al mecanicii clasice.

Principiul al II-lea al dinamicii se enunță în felul urmator: Forța este derivata de ordinul întâi al impulsului în raport cu timpul.

Forța netă asupra unei particule este astfel egală cu viteza de schimbare a impulsului particulei cu timpul. Deoarece definiția accelerației este a = dv/dt, a doua lege poate fi scrisă sub forma simplificată și mai familiară:

$\mathbf {F} =m\mathbf {a} \,$

Atâta timp cât este cunoscută forța care acționează asupra unei particule, a doua lege a lui Newton este suficientă pentru a descrie mișcarea unei particule. Odată ce relațiile independente pentru fiecare forță care acționează asupra unei particule sunt disponibile, ele pot fi înlocuite în a doua lege a lui Newton pentru a obține o ecuație diferențială obișnuită, care se numește ecuația mișcării.

Ca exemplu, presupunem că frecarea este singura forță care acționează asupra particulei și că poate fi modelată ca funcție a vitezei particulei, de exemplu:

$\mathbf {F} _{\rm {R}}=-\lambda \mathbf {v} \,,$

unde λ este o constantă pozitivă, semnul negativ afirmă că forța este opusă sensului vitezei. Atunci ecuația mișcării este

$-\lambda \mathbf {v} =m\mathbf {a} =m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}\,$

Acest lucru poate fi integrat pentru a obține

$\mathbf {v} =\mathbf {v} _{0}e^{\frac {-\lambda t}{m}}$

unde v₀ este viteza inițială. Aceasta înseamnă că viteza acestei particule scade exponențial la zero pe măsură ce timpul progresează. În acest caz, un punct de vedere echivalent este faptul că energia cinetică a particulei este absorbită prin frecare (ceea ce o transformă în energie termică în conformitate cu conservarea energiei), iar particula încetinește. Această expresie poate fi suplimentată pentru a obține poziția r a particulei în funcție de timp.

Lucrul mecanic și energia

Dacă o forță constantă F este aplicată asupra unei particule pe o distanță ${\textstyle \Delta }$r atunci lucrul mecanic efectuat de acea forță este egal cu produsul scalar dintre forță si distanța parcursă.

L = F $\cdot$ $\Delta$r

Într-un mod mai general, dacă forța variază ca o funcție de poziție, de la r₁ la r₂ de-a lungul unei curbe C, putem scrie astfel

$\int \limits _{C}$ F(r) dr

Dacă lucrul mecanic efectuat este același indiferent de drumul parcurs, atunci forța este conservativă. De exemplu forța de frecare este o forță neconservativă iar forța de greutate este conservativă.

Energia cinetică a unei particule de masă m și viteză v este dată de relația

E_c = ${\frac {1}{2}}\cdot$ m $\cdot$ v ²

Lucrul mecanic total efectuat asupra unui corp este egal cu variația energiei cinetice a acestuia, altfel spus L = $\Delta$E_c = E_cf $-$ E_ci

Forțele conservative pot fi exprimate de asemenea ca gradientul unei funcții scalare denumită energie potențială.

F = $-$$\nabla$E_p

Variația energiei potențiale este egală în modul cu variația energiei cinetice dar de semn opus.

$-\Delta$E_p = $\Delta$E_c $\rightarrow$ $\Delta$E = 0 (Variația energiei totale)

Relația anterioară este cunoscută drept Conservarea Energiei. De aici rezultă că variația energiei totale este constantă în timp.

$\sum$ E = E_c + E_p

Dincolo de legile lui Newton

Mecanica clasică descrie, de asemenea, mișcările mai complexe ale obiectelor non-punctiforme extinse. Legile lui Euler oferă extinderi la legile lui Newton în acest domeniu. Conceptul de moment cinetic se bazează pe același calcul folosit pentru a descrie mișcarea unidimensională. Ecuația lui Țiolkovski^⁠(d) extinde noțiunea de rată de schimbare a impulsului unui obiect, astfel încât să includă efectele unui obiect care „pierde masă”.

Există două formulări alternative importante ale mecanicii clasice: mecanica lagrangiană și mecanica hamiltoniană. Acestea și alte formulări moderne, ocolesc de obicei conceptul de „forță”, referindu-se în schimb la alte mărimi fizice, cum ar fi energia, viteza și impulsul, pentru descrierea sistemelor mecanice în coordonate generalizate.

Expresiile date mai sus pentru impuls și energie cinetică sunt valabile numai atunci când nu există o contribuție electromagnetică semnificativă. În electromagnetism, cea de-a doua lege a lui Newton pentru cabluri purtătoare de curent nu mai este valabilă, cu excepția cazului în care se include contribuția câmpului electromagnetic la impulsul sistemului așa cum este exprimat de vectorul Poynting împărțit la c², unde c este viteza luminii în spațiul liber.

Istorie

Articol principal: Istoria mecanicii clasice.

Studiul mișcării corpurilor este unul antic, făcând mecanica clasică una dintre cele mai vechi și mai mari materii în știință, inginerie și tehnologie.

Unii filosofi greci din antichitate, printre care Aristotel, fondatorul fizicii aristotelice, au fost primii care au menținut ideea că „totul se întâmplă pentru un motiv” și că principiile teoretice pot ajuta la înțelegerea naturii. Ulterior, teoria matematică și experimentul controlat au devenit factori decisivi în formarea științei moderne, iar aplicarea lor timpurie a devenit cunoscută sub numele de mecanică clasică.

Prima explicație cauzală publicată a mișcărilor planetelor a fost Astronomia nova a lui Johannes Kepler, publicată în 1609. El a concluzionat, pe baza observațiilor lui Tycho Brahe asupra orbitei lui Marte, că orbitele planetei sunt eliptice. Această rupere de gândirea antică se petrece în timp ce Galileo propune legi matematice abstracte pentru mișcarea obiectelor. Este posibil (sau nu) să fi făcut faimosul experiment de a arunca două bile de tun de greutăți diferite din turnul Pisa, arătând că ambele au lovit pământul în același timp. Realitatea acelui experiment special este contestată, însă el a efectuat experimente prin rularea bilelor pe un plan înclinat. Teoria sa despre mișcarea accelerată a fost derivată din rezultatele unor astfel de experimente și formează o piatră de temelie a mecanicii clasice.

Sir Isaac Newton (1643–1727), o figură influentă în istoria fizicii și ale cărui trei legi ale mișcării stau la baza mecanicii clasice.

Newton și-a întemeiat principiile filosofiei naturale pe trei legi ale mișcării: legea inerției, a doua sa lege a accelerației și legea acțiunii și reacțiunii. Atât a doua, cât și a treia lege a lui Newton au primit tratamentul științific și matematic adecvat în Philosophiæ Naturalis Principia Mathematica. Legile se disting de încercările anterioare de a explica fenomene similare, încercări care au fost fie incomplete, incorecte, fie au propus o expresie matematică inexactă. Newton a enunțat, de asemenea, principiile conservării impulsului și a momentului cinetic. În mecanică, Newton a fost, de asemenea, primul care a furnizat prima formulare științifică și matematică corectă a gravitației în Legea atracției universale. Combinația dintre legile de mișcare și gravitație ale lui Newton oferă descrierea cea mai completă și cea mai exactă a mecanicii clasice. El a demonstrat că aceste legi se aplică atât obiectelor cotidiene, cât și obiectelor cerești. În special, el a obținut o explicație teoretică a legilor lui Kepler de mișcare a planetelor.

Cea mai mare contribuție a lui Hamilton este probabil reformularea mecanicii newtoniene, numită astăzi mecanică hamiltoniană.

Newton și majoritatea contemporanilor săi, cu excepția notabilă a lui Huygens, au presupus că mecanica clasică va fi în măsură să explice toate fenomenele, inclusiv lumina, sub forma opticii geometrice. Chiar când a descoperit așa-numitele inele ale lui Newton (un fenomen de interferență a undelor), el și-a menținut propria teorie corpusculară a luminii.

După Newton, mecanica clasică a devenit un domeniu principal de studiu atât în matematică, cât și în fizică. Câteva re-formulări au permis progresiv găsirea de soluții la un număr mare de probleme. Prima re-formulare notabilă a fost în 1788 de Joseph Louis Lagrange. Mecanica lagrangiană a fost, la rândul ei, re-formulată în 1833 de William Rowan Hamilton.

La sfârșitul secolului al XIX-lea au fost descoperite unele dificultăți care nu puteau fi soluționate decât de o fizică mai modernă. Unele dintre aceste dificultăți au fost legate de compatibilitatea cu teoria electromagnetică și celebrul experiment Michelson – Morley. Rezolvarea acestor probleme a dus la teoria restrânsă a relativității, adesea considerată parte a mecanicii clasice.

Un al doilea set de dificultăți au fost legate de termodinamică. Când este combinată cu termodinamica mecanica clasică duce la paradoxul Gibbs al mecanicii statistice clasice, în care entropia nu este o cantitate bine definită. Radiația corpului negru nu a fost explicată fără introducerea cuantei. Pe măsură ce experimentele au atins nivelul atomic, mecanica clasică nu a reușit să explice, nici măcar aproximativ, lucruri de bază precum nivelul de energie și dimensiunile atomilor și efectul fotoelectric. Efortul de soluționare a acestor probleme a dus la dezvoltarea mecanicii cuantice.

De la sfârșitul secolului XX, mecanica clasică în fizică nu a mai fost o teorie independentă. În schimb, mecanica clasică este considerată acum o teorie aproximativă a mecanicii cuantice mai generale. Accentul a trecut la înțelegerea forțelor fundamentale ale naturii ca în Modelul Standard și extensiile sale mai moderne într-o teorie a întregului. Mecanica clasică este o teorie utilă pentru studiul mișcării particulelor mecanice non-cuantice, cu energie redusă în câmpuri gravitaționale slabe. De asemenea, a fost extinsă în domeniul complex, unde mecanica clasică complexă prezintă comportamente foarte similare cu mecanica cuantică.

Legături externe

• ro Dumitru Luca, Cristina Stan: "Curs de mecanică clasică"