16-celule
| 16-celule regulat (4-ortoplex) | |
 Diagramă Schlegel (vârfuri și laturi) | |
| Tip | 4-politop regulat convex |
|---|---|
| Simbol Schläfli | {3,3,4} |
| Diagramă Coxeter | |
| Celule | 16 {3,3} |
| Fețe | 32 {3} |
| Laturi | 24 |
| Vârfuri | 8 |
| Figura vârfului |  Octaedru |
| Poligon Petrie | octogon |
| Grup Coxeter | B4, [3,3,4], ordinul 384 D4, ordinul 192 |
| Dual | Tesseract |
| Proprietăți | convex, izogonal, izotoxal, izoedric |
| Index uniform | 12 |

În geometrie 16-celule[a] este un obiect din spațiul cvadridimensional, fiind mărginit de de 16 celule tetraedrice. Este unul dintre cele șase 4-politopuri convexe regulate descrise pentru prima dată de matematicianul elvețian Ludwig Schläfli la mijlocul secolului al XIX-lea. Mai este cunoscut sub numele de 4-ortoplex sau C16.[1]
Face parte din familia infinită de ortoplecși și este analog cu octaedrul din trei dimensiuni. Este politopul notat de Coxeter .[2] Numele de ortoplex i-a fost dat de Conway. Politopul său dual este tesseractul (4-cubul), cu care se poate combina formând compusul de tesseract și 16-celule. 16-celule are 16 celule după cum tesseractul are 16 vârfuri.
Geometrie
[modificare | modificare sursă]Este mărginit de 16 celule, toate fiind tetraedre regulate. Are 32 de fețe triunghiulare, 24 de laturi și 8 vârfuri. Cele 24 de laturi mărginesc 6 pătrate din cele 6 plane ale coordonatelor.
Cele opt vârfuri ale unui 16-celule au coordonatele (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). Toate vârfurile sunt conectate prin laturi, cu excepția perechilor de vârfuri opuse.
Simbolul Schläfli al unui 16-celule este {3,3,4}. Figura vârfului său este un octaedru regulat. În fiecare vârf se întâlnesc câte 8 tetraedre, 12 triunghiuri și 6 laturi. Figura laturii este un pătrat. Pe fiecare latură se întâlnesc 4 tetraedre și 4 triunghiuri.
16-celule poate fi descompus în două lanțuri circulare disjuncte similare de câte opt tetraedre, fiecare lanț având lungimea a patru muchii. Fiecare lanț, atunci când este întins drept, formează o elice Boerdijk–Coxeter. Această descompunere poate fi văzută într-o construcție a unei 4-4 duoantiprisme a 16-celule: ![]()
![]()
![]()
![]()
![]()
![]()
![]() sau
sau ![]()
![]()
![]()
![]()
![]()
![]()
![]() , simbol Schläfli {2}⨂{2} sau s{2}s{2}, simetrie 4,2+,4, ordinul 64.
, simbol Schläfli {2}⨂{2} sau s{2}s{2}, simetrie 4,2+,4, ordinul 64.
Un 16-celule poate fi divizat în două piramide octaedrice, care au în comun o nouă bază octaedrică prin centrul 16-celulei.
Configurație
[modificare | modificare sursă]Un 16-celule poate fi descris de o matrice de configurație care conține numărul elementelor sale componente. Rândurile și coloanele corespund vârfurilor, laturilor, fețelor și celulelor. Numerele de pe diagonala principală (din stânga sus în dreapta jos) arată câte din fiecare tip de element apar în întregul 16-celule. Celelalte numere arată câte elemente ale coloanei apar pentru sau la elementul rândului. de o matrice a configurației.
Imagini
[modificare | modificare sursă]
|

|

|
| Proiecție 3D a unui 16-celule executând o rotație simplă |
Proiecție 3D a unui 16-celule executând o rotație |
Proiecție stereografică |
Proiecții ortogonale
[modificare | modificare sursă]| Planul Coxeter | B4 | B3 / D4 / A2 | B2 / D3 | F4 | A3 |
|---|---|---|---|---|---|
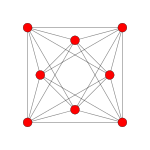
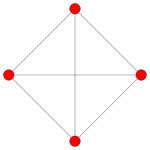
| Graf | 
|

|

|
|
|
| Simetrie diedrală | [8] | [6] | [4] | [12/3] | [4] |
Teselări
[modificare | modificare sursă]Spațiul cvadridimensional euclidian poate fi teselat cu 16-celule regulate. Aceasta se numește fagure 16-celule și are simbolul Schläfli {3,3,4,3}. Prin urmare, 16-celule are un unghi diedru de 120°.[3] Fiecare 16-celule are 16 vecini cu care are în comun un tetraedru, 24 vecini cu care are în comun o latură și 72 de vecini cu care are în comun doar câte un singur punct. 24 de 16-celule se întâlnesc în fiecare vârf al aceastei teselări.
Teselarea duală este fagurele 24-celule, {3,4,3,3}, format din 24-celule regulate. Împreună cu fagurele teseractic, {4,3,3,4}, acestea sunt singurele trei teselări regulate din R< sup>4.
Elicea Boerdijk–Coxeter
[modificare | modificare sursă]
Un 16-celule poate fi construit din două elice Boerdijk–Coxeter formate din câte opt tetraedre, fiecare lanț fiind pliat într-un inel cvadridimensional. Cele 16 fețe triunghiulare pot fi văzute într-o desfășurată 2D într-o pavare triunghiulară, cu 6 triunghiuri în jurul fiecărui vârf. Marginile purpurii reprezintă poligonul Petrie al 16-celulei.
Proiecții
[modificare | modificare sursă]
Proiecția ortogonală în 3-spațiu a unui 16-celule cu o celulă în față are o anvelopă cubică. Celula cea mai apropiată și cea ma depărtată sunt proiectate prin tetraedrele înscrise în cub, corespunzând celor două posibilități de a înscrie un tetraedru regulat într-un cub. În jurul fiecăruia dintre aceste două tetraedre sunt alte 4 volume tetraedrice (neregulate), care sunt imaginile celor 4 celule tetraedrice din jur, umplând spațiul dintre tetraedrul încris și cub. Restul de 6 celule sunt proiectate pe fețele pătrate ale cubului. În această proiecție a 16-celulei, toate marginile sale se află pe fețele anvelopei cubice.
Proiecția în perspectivă cu o celulă în față are o anvelopă tetraedrică trakis. Dispunerea celulelor din acest anvelopă este analoagă cu cea a proiecției paralele cu o celulă în față.
Proiecția ortogonală cu o față în față are o anvelopă bipiramidă hexagonală, iar proiecția ortogonală cu o latură în față are o anvelopă oactaedrică scrurtată.
Proiecția ortogonală cu un vârf în față are o anvelopă octaedrică. Acest octaedru poate fi împărțit în 8 volume tetraedrice, prin tăierea de-a lungul planelor coordonatelor. Fiecare dintre aceste volume este imaginea unei perechi de celule din 16-celule. Cel mai apropiat vârf al 16-celulei se proiectează în centrul octaedrului.
Diagrama Venn a 4-sferei
[modificare | modificare sursă]proiecția unui 16-celule având aceeași orientare
Proiecția tridimensională a 16-celule și a 4-sferă care se intersectează (o diagramă Venn de 4 seturi) sunt topologic echivalente:
Construcții cu diferite simetrii
[modificare | modificare sursă]Există o formă a 16-celule cu un număr inferior de simetrii, numită semitesseract sau 4-semicub, un membru al familiei semihipercuburilor, reprezentată de h{4,3,3} și diagramele Coxeter ![]()
![]()
![]()
![]()
![]()
![]()
![]() sau
sau ![]()
![]()
![]()
![]()
![]() . Aceasta pot fi colorată bicolor alternând celulele tetraedriece.
. Aceasta pot fi colorată bicolor alternând celulele tetraedriece.
Poate fi văzut și sub formă de antiprismă tetraedrică, tot cu un număr inferior de simetrii, construit din 2 tetraedre paralele în configurații duale, conectate prin 8 tetraedre (posibil alungite). Este reprezentat de s{2,4,3} și diagrama Coxeter: ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Poate fi văzut și ca un 4-hiperdreptunghi snub, reprezentat de s{21,1,1} și diagramele Coxeter: ![]()
![]()
![]()
![]()
![]()
![]()
![]() sau
sau ![]()
![]()
![]()
![]()
![]() .
.
Considerând tesseractul ca fiind o 4-4 duoprismă, 16-celule poate fi văzut ca dualul său, o 4-4 duopiramidă.
| Nume | Diagramă Coxeter | Simbol Schläfli | Notația Coxeter | Ordin | Figura vârfului |
|---|---|---|---|---|---|
| 16-celule regulat | {3,3,4} | [3,3,4] | 384 | ||
| Semitesseract 16-celule cvasiregulat |
h{4,3,3} {3,31,1} |
[31,1,1] = [1+,4,3,3] | 192 | ||
| 4-4 duoprismă alternată | 2s{4,2,4} | [[4,2+,4]] | 64 | ||
| Antiprismă tetraedrică | s{2,4,3} | [2+,4,3] | 48 | ||
| Prismă pătrată prismatică alternată | sr{2,2,4} | [(2,2)+,4] | 16 | ||
| 4-hiperdreptunghi snub | s{21,1,1} | [2,2,2]+ = [21,1,1]+ | 8 | ||
| 4-fusil | |||||
| {3,3,4} | [3,3,4] | 384 | |||
| {4}+{4} or 2{4} | [[4,2,4]] = [8,2+,8] | 128 | |||
| {3,4}+{ } | [4,3,2] | 96 | |||
| {4}+2{ } | [4,2,2] | 32 | |||
| { }+{ }+{ }+{ } or 4{ } | [2,2,2] | 16 |
Poligoane complexe asociate
[modificare | modificare sursă]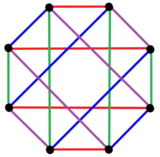
|

|
| În planul Coxeter B4, 2{4}4 are 8 vârfuri și 16 laturi, în 4 seturi colorate diferit. | Cele 8 vârfuri sunt grupate în 2 seturi (roșu și albastru), fiecare vârf fiind conectat prin laturi doar la vârfurile din celălalt set, făcând ca acest poligon să fie un graf bipartit complet, K4,4.[4] |
Poligonul Möbius–Kantor este un poligon complex regulat 3{3}3, ![]()
![]()
![]() , în are aceleași vârfuri cu 16-celule. Are 8 vârfuri și 8 3-fețe.[5][6]
, în are aceleași vârfuri cu 16-celule. Are 8 vârfuri și 8 3-fețe.[5][6]
Poligonul complex regulat 2{4}4, ![]()
![]()
![]() , în are o reprezentare reală ca 16-celule în spațiul cvadridimensional, cu 8 vârfuri, 16 laturi (2-fețe), doar jumătate din laturile unui 16-celule. Simetria sa este 4[4]2, ordinul 32.[7]
, în are o reprezentare reală ca 16-celule în spațiul cvadridimensional, cu 8 vârfuri, 16 laturi (2-fețe), doar jumătate din laturile unui 16-celule. Simetria sa este 4[4]2, ordinul 32.[7]
Politopuri și faguri uniformi asociați
[modificare | modificare sursă]16-celule regulat împreună cu tesseractul fac parte dintr-un set de 15 4-politopuri uniforme cu aceeași simetrie. De asemenea, face parte dintre politopurile uniforme cu simetria D4.
De asemenea, acest 4-politop este legat de fagurele cubic, fagurele dodecaedric de ordinul 4 și fagurele pavare hexagonală de ordinul 4 care toate au figuri ale vârfului octaedriece.
Este într-o secvență de 4-politopuri regulate: împreună cu 5-celule {3,3,3}, 600-celule {3,3,5} din 4-spațiul euclidian și cu fagurele tetraedric de ordinul 6 {3,3,6} din spațiu hiperbolic. Toți aceștia au celule tetraedrice.
Este primul din secvența politopurilor și fagurilor cvasiregulați h{4,p,q} și a secvenței formelor cu simetria pe jumătate {p,3,4} regulate.
Note explicative
[modificare | modificare sursă]- ^ „16-celule” este o prescurtare a expresiei din limba română „un politop cvadridimensional format din 16 celule”, plural „două sau mai multe politopuri cvadridimesnsionale formate din câte 16 celule”, expresii care se acordă corespunzător, deci se vorbește despre „un/acel 16-celule”, nu „o/acea 16-celule”, respectiv „unele/acele 16-celule”', nu „unii/acei 16-celule”. La fel la celelalte politopuri ale căror nume este de forma „n-celule”.
Note
[modificare | modificare sursă]- ^ en N.W. Johnson: Geometries and Transformations, (2018) ISBN: 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249
- ^ Coxeter 1973, p. 121, §7.21. see illustration Fig 7.2B.
- ^ Coxeter 1973, p. 293.
- ^ Regular Complex Polytopes, p. 114
- ^ Coxeter, Shephard, 1991, p. 30, 47
- ^ Coxeter, Shephard, 1992
- ^ Regular Complex Polytopes, p. 108
Bibliografie
[modificare | modificare sursă]- en T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- en H.S.M. Coxeter:
- Coxeter, H.S.M. (). Regular Polytopes (ed. 3rd). New York: Dover.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- en Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
Legături externe
[modificare | modificare sursă] Materiale media legate de 16-celule la Wikimedia Commons
Materiale media legate de 16-celule la Wikimedia Commons- en Eric W. Weisstein, 16-Cell la MathWorld.
- de Der 16-Zeller (16-cell) Marco Möller's Regular polytopes in R4
- en Description and diagrams of 16-cell projections Arhivat în , la Wayback Machine.
- en Klitzing, Richard. „4D uniform polytopes (polychora) x3o3o4o - hex”.
| Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familie | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Poligoane regulate | Triunghi | Pătrat | p-gon | Hexagon | Pentagon | |||||||
| Poliedre uniforme | Tetraedru | Octaedru • Cub | Semicub | Dodecaedru • Icosaedru | ||||||||
| 4-politopuri uniforme | 5-celule | 16-celule • Tesseract | Semitesseract | 24-celule | 120-celule • 600-celule | |||||||
| 5-politopuri uniforme | 5-simplex | 5-ortoplex • 5-cub | 5-semicub | |||||||||
| 6-politopuri uniforme | 6-simplex | 6-ortoplex • 6-cub | 6-semicub | 122 • 221 | ||||||||
| 7-politopuri uniforme | 7-simplex | 7-ortoplex • 7-cub | 7-semicub | 132 • 231 • 321 | ||||||||
| 8-politopuri uniforme | 8-simplex | 8-ortoplex • 8-cub | 8-semicub | 142 • 241 • 421 | ||||||||
| 9-politopuri uniforme | 9-simplex | 9-ortoplex • 9-cub | 9-semicub | |||||||||
| 10-politopuri uniforme | 10-simplex | 10-ortoplex • 10-cub | 10-semicub | |||||||||
| n-politopuri uniforme | n-simplex | n-ortoplex • n-cub | n-semicub | 1k2 • 2k1 • k21 | n-politop pentagonal | |||||||
| Topicuri: Familii de politopuri • Politop regulat | ||||||||||||










