Fagure cubic

Fagure cubic

Tip	fagure regulat, din familia fagurilor hipercubici
Simbol Schläfli	{4,3,4}
Diagramă Coxeter
Celule	{4,3}
Fețe	pătrat {4}
Laturi	[{4,3}]⁴
Figura vârfului	(octaedru)
Grup Coxeter	${\tilde {C}}_{3}$ , [4,3,4]
Grup de simetrie	Pm3m (221)
Dual	autodual
Proprietăți	Fagure regulat, convex, tranzitiv pe vârfuri, laturi și fețe
Index uniform	J_11,15, A₁, W₁, G₂₂^[1]

Un fagure cubic este singura teselare regulată (sau fagure) a spațiului euclidian tridimensional cu celule cubice. Este tranzitiv pe vârfuri, având câte 8 cuburi în jurul fiecărui vârf. Este tranzitiv pe laturi, cu câte 4 cuburi în jurul fiecărei laturi. De asemenea, este tranzitiv pe fețe, cu câte 2 cuburi în jurul fiecărei fețe. Este autodual, cu simbolul Schläfli {4,3,4}.

Faguri înrudiți[modificare | modificare sursă]

Face parte dintr-o familie multidimensională de faguri hipercubici, cu simboluri Schläfli de forma {4,3,...,3,4}, începând cu pavarea pătrată {4,4} în plan.

Este unul dintre cei 28 de faguri uniformi convecși^⁠(d) cu celule poliedre uniforme convexe.

Izometriile rețelelor cubice simple[modificare | modificare sursă]

Rețelele cubice simple pot fi distorsionate în simetrii inferioare, reprezentate de sisteme cristaline inferioare:

Sistem cristalin	Monoclinic Triclinic	Ortorombic	Tetragonal	Hexagonal	Cubic
Celulă	Paralelipiped	Cuboid dreptunghic	Cuboid pătrat	Trapezoedru trigonal	Cub
Grup punctual^⁠(d) Ordin Subgrup de rotație	[ ], (*) Ordin 2 [ ]⁺, (1)	[2,2], (*222) Ordin 8 [2,2]⁺, (222)	[4,2], (*422) Ordin 16 [4,2]⁺, (422)	[3], (*33) Ordin 6 [3]⁺, (33)	[4,3], (*432) Ordin 48 [4,3]⁺, (432)
Formă
Grup spațial^⁠(d) Subgrup de rotație	Pm (6) P1 (1)	Pmmm (47) P222 (16)	P4/mmm (123) P422 (89)	R3m (160) R3 (146)	Pm3m (221) P432 (207)
Notația Coxeter	-	[∞]_a×[∞]_b×[∞]_c	[4,4]_a×[∞]_c	-	[4,3,4]_a
Diagramă Coxeter	-			-

Colorare uniformă[modificare | modificare sursă]

Există un număr mare de colorări uniforme, derivate din diferite simetrii. Acestea includ:

Notația Coxeter Grup spațial	Diagramă Coxeter	Simbol Schläfli	Culorile pe litere
[4,3,4] Pm3m (221)	=	{4,3,4}	1: aaaa/aaaa
[4,3^1,1] = [4,3,4,1⁺] Fm3m (225)	=	{4,3^1,1}	2: abba/baab
[4,3,4] Pm3m (221)		t_0,3{4,3,4}	4: abbc/bccd
[[4,3,4]] Pm3m (229)		t_0,3{4,3,4}	4: abbb/bbba
[4,3,4,2,∞]	or	{4,4}×t{∞}	2: aaaa/bbbb
[4,3,4,2,∞]		t₁{4,4}×{∞}	2: abba/abba
[∞,2,∞,2,∞]		t{∞}×t{∞}×{∞}	4: abcd/abcd
[∞,2,∞,2,∞] = [4,(3,4)^*]	=	t{∞}×t{∞}×t{∞}	8: abcd/efgh

Proiecții[modificare | modificare sursă]

Fagurele cubic poate fi proiectat ortogonal în planul euclidian cu diverse aranjamente de simetrie. Cea mai înaltă formă de simetrie (hexagonală) se proiectează într-o pavare triunghiulară. O proiecție cu simetrie pătrată formează o pavare pătrată.

Proiecții ortogonale
Simetrie	p6m (*632)	p4m (*442)	pmm (*2222)
Imagine
Cadru de sârmă

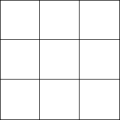
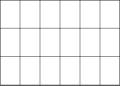
Politopuri și faguri înrudiți[modificare | modificare sursă]

Este înrudit cu 4-politopul regulat tesseract, simbol Schläfli {4,3,3}, care există în spațiul cvadridimensional și are doar 3 cuburi în jurul fiecărei laturi. Este, de asemenea, legat de fagurele cubic de ordinul 5, simbolul Schläfli {4,3,5}, din spațiul hiperbolic, cu 5 cuburi în jurul fiecărei laturi.

Apare în succesiunea de politopuri și faguri cu figura vârfului octaedrul:

Faguri regulați {p,3,4}
Spațiu	S³	E³	H³
Formă	Finit	Afin	Compact	Paracompact	Necompact
Nume	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	... {∞,3,4}
Imagine
Celule	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Face parte din șirul de politopuri regulate și faguri cu celule cubice:

Faguri regulați {4,3,p}
Spațiu	S³	E³	H³
Formă	Finit	Afin	Compact	Paracompact	Necompact
Nume	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	... {4,3,∞}
Imagine
Figura vârfului	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Faguri regulați {p,3,p}
Spațiu	S³	E³	H³
Formă	Finit	Afin	Compact	Paracompact	Necompact
Nume	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Imagine
Celule	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Figura vârfului	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Note[modificare | modificare sursă]

^ en For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).

Bibliografie[modificare | modificare sursă]

en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN: 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
en H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8 p. 296, Table II: Regular honeycombs
en George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
en Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6 [1]

(Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)

it Alfredo Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative, Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
en Klitzing, Richard. „3D Euclidean Honeycombs x4o3o4o - chon - O1”.
en Uniform Honeycombs in 3-Space: 01-Chon
en The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN: 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space Arhivat în 10 iunie 2016, la Wayback Machine.) Table III
en Norman Johnson, Ruth Kellerhals, J. G. Ratcliffe, S. T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H³: p130. [2]

Portal Matematică

v • d • m Faguri convecși regulați și uniformi în dimensiunile 2–8
Spațiu	Familia	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
E²	Pavare uniformă	{3^[3]}	δ₃	hδ₃	qδ₃	Hexagonală
E³	Fagure convex uniform	{3^[4]}	δ₄	hδ₄	qδ₄
E⁴	4-fagure uniform	{3^[5]}	δ₅	hδ₅	qδ₅	Fagure 24-celule
E⁵	5-fagure uniform	{3^[6]}	δ₆	hδ₆	qδ₆
E⁶	6-fagure uniform	{3^[7]}	δ₇	hδ₇	qδ₇	2₂₂
E⁷	7-fagure uniform	{3^[8]}	δ₈	hδ₈	qδ₈	1₃₃ • 3₃₁
E⁸	8-fagure uniform	{3^[9]}	δ₉	hδ₉	qδ₉	1₅₂ • 2₅₁ • 5₂₁
E^n-1	(n−1)-fagure uniform	{3^[n]}	δ_n	hδ_n	qδ_n	1_k2 • 2_k1 • k₂₁

[1] For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).

[1]