Coordonate polare

În matematică, sistemul de coordonate polare este un sistem de coordonate bidimensional în care fiecărui punct din plan i se asociază un unghi și o distanță. Sistemul coordonatelor polare este util mai ales în situații în care relația dintre două puncte este mai ușor de exprimat în funcție de distanțe și direcții (unghiuri); în sistemul cartezian sau ortogonal, o astfel de relație poate fi găsită doar cu ajutorul formulelor trigonometrice.
Deoarece sistemul de coordonate este bidimensional, fiecare punct este determinat de două coordonate polare: coordonata radială și coordonata unghiulară. Coordonata radială (notată de obicei cu r) reprezintă distanța unui punct față de un punct central, numit pol (echivalent cu originea din sistemul cartezian). Coordonata unghiulară (cunoscută și sub numele de unghi polar, sau azimut, și notată cu θ sau t) reprezintă unghiul, în sens trigonometric sau invers orar (invers acelor de ceasornic) necesar pentru a ajunge la el de la direcția de 0°, numită axa polară (echivalentă cu axa absciselor din coordonatele carteziene plane).[1]
Istoric[modificare | modificare sursă]
Conceptele de unghi și rază erau deja folosite de popoarele antice din primul mileniu î.e.n.. Astronomul grec Hipparchus (190–120 î.e.n.) este creatorul unei tabele de funcții armonice care dădeau lungimea unui arc pentru fiecare unghi, și există unele referințe despre utilizarea de către el a coordonatelor polare pentru stabilirea poziției stelelor.[2] În Despre spirale, Arhimede descrie Spirala lui Arhimede, o funcție a cărei rază depinde de unghi. Lucrările grecești, însă, nu s-au extins la un întreg sistem de coordonate.
Începând cu secolul al VIII-lea e.n., astronomii au dezvoltat metode de aproximare și calcul al direcției către Mecca (qibla)—și a distanței până acolo—din orice loc de pe Pământ.[3] Prin secolul al IX-lea începeau să folosească metode de trigonometrie sferică și proiecție cartografică pentru a determina cu precizie aceste valori. Calculul era în esență o transformare a coordonatelor polare ecuatoriale(d) ale Meccăi (adică longitudinea și latitudinea) în coordonate polare (adică qibla și distanța) relative la un sistem al cărui meridian de referință era marele cerc ce trecea prin locația dată și prin polii Pământului și a cărui axă polară este linia ce trece prin locația respectivă și prin punctul său antipodal.[4]
Există mai multe relatări despre introducerea coordonatelor polare ca parte dintr-un sistem oficial. Întreaga istorie este descrisă de profesorul Julian Coolidge(d) de la Universitatea Harvard în lucrarea sa Originea coordonatelor polare.[5] Grégoire de Saint-Vincent și Bonaventura Cavalieri au introdus independent unul de altul aceste concepte la jumătatea secolului al XVII-lea. Saint-Vincent scria despre ele în particular în 1625 și își publică lucrarea în 1647, iar Cavalieri în 1635, cu o versiune corectată apărută în 1653. Cavalieri a utilizat primul coordonatele polare pentru a rezolva o problemă legată de aria din interiorul unei spirale a lui Arhimede. Ulterior, Blaise Pascal a utilizat coordonate polare pentru calculul arcelor parabolice.
Sir Isaac Newton a examinat și el transformările în coordonate polare, pe care le-a denumit "Al șaptelea mod; pentru spirale", și nouă alte sisteme de coordonate.[6] Într-un articol din periodicul Acta Eruditorum (1691), Jakob Bernoulli folosea un sistem cu un punct pe o linie,[7] numite pol, respectiv axă polară. Coordonatele erau specificate prin distanța de la pol și unghiul față de axa polară. Lucrarea lui Bernoulli se ocupă de găsirea razei de curbură a curbelor exprimate în aceste coordonate.
Termenul efectiv coordonate polare îi este atribuit lui Gregorio Fontana și era utilizat de scriitorii italieni ai secolului al XVIII-lea. Alexis Clairaut a fost primul care s-a gândit la o generalizare a coordonatelor polare în trei dimensiuni, iar Leonhard Euler a fost primul care le-a dezvoltat.[5]
Trasarea punctelor în coordonate polare[modificare | modificare sursă]

Fiecare punct din sistemul de coordonate polare poate fi descris folosind două coordonate polare, numite uzual r (coordonata radială) și θ (coordonata unghiulară, unghiul polar, sau azimutul, uneori reprezentat ca φ sau t). Coordonata r reprezintă distanța radială de pol, și coordonata θ reprezintă unghiul în sens trigonometric (invers acelor de ceasornic) de la direcția de 0° (numită uneori axă polară), cunoscută ca axa pozitivă a absciselor în sistemul coordonatelor carteziene plane.[1]
De exemplu, coordonatele polare (3, 60°) ar fi reprezentate în plan ca un punct aflat la 3 unități depărtare de pol pe direcția de 60°. Coordonatele (−3, 240°) ar fi reprezentate prin același punct deoarece o distanță radială negativă este măsurată ca o distanță pozitivă pe aceeași direcție în sens opus (direcția reflectată față de origine, care diferă de direcția originară cu 180°).
Aceasta ilustrează un aspect important al sistemului de coordonate polare, aspect care lipsește la cel cartezian: un singur punct poate fi exprimat printr-o infinitate de coordonate diferite. În general, punctul (r, θ) poate fi reprezentat ca (r, θ ± n × 360°) sau ca (−r, θ ± (2n + 1)180°), unde n este orice număr întreg.[8] Coordonatele arbitrare (0, θ) sunt utilizate prin convenție pentru reprezentarea polului, pentru că indiferent de coordonata θ, un punct de rază 0 va fi mereu în pol.[9] Pentru a obține o reprezentare unică a unui punct, este uzual a limita r la numere nenegative r ≥ 0 și pe θ la intervalul [0, 360°) sau (−180°, 180°] (sau, în radiani, [0, 2π) sau (−π, π]).[10]
Unghiurile în notație polară sunt în general exprimate fie în grade, fie în radiani, utilizând conversia 2π rad = 360°. Alegerea depinde de context. Aplicațiile nautice folosesc gradele, în timp ce unele aplicații din fizică (mai ales mecanica rotației) și aproape toată literatura matematică legată de analiza matematică folosesc radiani.[11]
Conversia între coordonate polare și coordonate carteziene[modificare | modificare sursă]

Cele două coordonate polare r și θ pot fi convertite în coordonate carteziene x și y prin utilizarea funcțiilor trigonometrice sinus și cosinus:
în timp ce două coordonate carteziene x și y pot fi transformate în coordonata polară r prin
- (prin aplicarea teoremei lui Pitagora).
Pentru a determina coordonata polară θ, trebuie să fie luate în considerare următoarele două aspecte:
- Pentru r = 0, θ poate fi orice număr real.
- Pentru r ≠ 0, pentru a obține o unică reprezentare a lui θ, aceasta trebuie limitată la un interval de lungime 2π. Alegeri convenționale pentru acest interval sunt [0, 2π) și (−π, π].
Pentru a obține θ în intervalul [0, 2π), se poate folosi următoarea expresie ( reprezintă inversa funcției tangentă):
Pentru a obține θ în intervalul (−π, π], se poate folosi următoarea expresie:[12]
Ecuații polare[modificare | modificare sursă]
Ecuațiile care definesc o curbă algebrică exprimată în coordonate polare este o ecuație polară. În multe cazuri, o astfel de ecuație poate fi specificată doar prin definirea r ca funcție de θ. Curba rezultată constă atunci din punctele de forma (r(θ), θ) și poate fi privită ca graficul funcției polare r.
Diferite forme de simetrie pot fi deduse din ecuația unei funcții polare . Dacă r(−θ) = r(θ), curba va fi simetrică față de direcția orizontală (0°/180°); dacă r(π−θ) = r(θ), ea va fi simetrică față de verticală (90°/270°); iar dacă r(θ−α°) = r(θ) ea va avea simetrie radială de α° în sens trigonometric în jurul polului.
Deoarece natura circulară a sistemului coordonatelor polare, multe curbe pot fi descrise de o ecuație polară relativ simplă, pe când forma lor carteziană e mult mai complicată. Printre cele mai cunoscute astfel de curbe este roza polară, spirala lui Arhimede, lemniscata lui Bernoulli, melcul lui Pascal, și cardioida.
Cercul[modificare | modificare sursă]

Ecuația generală a unui cerc cu centrul în (r0, φ) și de rază a este
Aceasta poate fi simplificată în numeroase feluri, pentru a se conforma unor cazuri particulare, cum ar fi ecuația
pentru un cerc cu centrul în pol și de rază a.[13]
Dreapta[modificare | modificare sursă]
Dreptele radiale (cele care trec prin pol) sunt reprezentate de ecuația
- ,
unde φ este unghiul de înclinație a dreptei; adică, φ = arctan m unde m este panta dreptei în coordonate carteziene. Dreapta neradială perpendiculară pe dreapta radială θ = φ în punctul (r0, φ) are ecuația
Roza polară[modificare | modificare sursă]

Roza polară este o curbă matematică celebră care arată ca o floare cu petale și care poate fi exprimată ca o ecuație polară simplă,
pentru orice constantă (inclusiv 0). Dacă n este întreg, această ecuație produce o roză cu n petale, dacă n este impar, sau cu 2n petale dacă este par. Dacă n este rațional dar nu întreg, o formă asemănătoare cu roza ar putea apărea, dar va avea petale suprapuse. Dacă n este irațional, curba formează un disc deoarece fiecare punct din planul de coordonate cu va satisface ecuația pentru o oarecare valoare a lui . Se observă că aceste ecuații nu definesc niciodată o roză cu 2, 6, 10, 14, etc. petale. Variabila a reprezintă lungimea petalelor rozei.
Spirala lui Arhimede[modificare | modificare sursă]

Spirala lui Arhimede este o spirală celebră descoperită de Arhimede, spirală ce poate fi exprimată sub forma unei ecuații polare simple. Ea este reprezentată de ecuația:
Schimbarea parametrului a va roti spirala, pe când b controlează distanța dintre brațe, care pentru o spirală dată este mereu constantă. Spirala lui Arhimede are două brațe, unul pentru θ > 0 și unul pentru θ < 0. Cele două brațe sunt conectate la origine și spirala este derivabilă în acel punct. Luând imaginea în oglindă a unui braț al său peste linia de la 90°/270° se obține un alt braț. Această curbă este notabilă ca una din primele curbe, după secțiunile conice, care a fost descrisă într-un tratat matematic, și ca prim exemplu de curbă mai bine definită sub formă de ecuație polară.
Secțiuni conice[modificare | modificare sursă]

O secțiune conică cu un focar în origine și celălalt undeva pe semidreapta de 0° (astfel încât axa majoră este în lungul axei polare) este dată de:
unde e este excentricitatea și distanța perpendiculară la focar de la axa majoră la curbă. Dacă e > 1, această ecuație definește o hiperbolă; dacă e = 1, ea definește o parabolă; iar dacă e < 1, definește o elipsă. Cazul special e = 0 are ca rezultat un cerc de rază .
Numere complexe[modificare | modificare sursă]

Toate numerele complexe pot fi reprezentate ca un punct în planul complex, și pot astfel să fie exprimate specificând fie coordonatele carteziene ale punctului, fie pe cele polare (numite formă polară). Numărul complex z poate fi reprezentat în formă carteziană ca
unde i este unitatea imaginară, sau poate fi scris în formă polară (trigonometrică)
și de aici ca
unde e este numărul lui Euler. Acestea sunt echivalente conform formulei lui Euler.[14] (Această formulă, ca orice formulă care implică exponențialele unor unghiuri, presupune că θ este exprimat în radiani.)


Formula lui Euler, evidențiată prima dată de Roger Cotes în formă logaritmică, face conversia între forma carteziană și cea polară a unui număr complex.
Pentru operațiile de înmulțire, împărțire, și exponențiere de numere complexe, este în general mai simplu de lucrat cu numere complexe exprimate în formă polară decât în formă carteziană prin proprietățile exponențierii:
- Înmulțire:
- Împărțire:
- Exponențiere (Formula lui de Moivre):
Analiza matematică[modificare | modificare sursă]
Se poate aplica analiză matematică pe ecuațiile exprimate în coordonate polare.[15][16]
Coordonata unghiulară θ este exprimată în radiani, alegere standard în analiza matematică.
Calcul diferențial[modificare | modificare sursă]
Sunt valabile formulele:
Pentru a găsi panta carteziană a tangentei la o curbă polară r(θ) în orice punct dat, curba este întâi exprimată ca sistem de ecuații parametrice.
Derivând ambele ecuații în raport cu θ rezultă
Împărțind a doua ecuație la prima, rezultă panta carteziană a tangentei la curbă în punctul (r, r(θ)):
Calcul integral[modificare | modificare sursă]

Fie R regiunea cuprinsă între o curbă r(θ) și razele θ = a și θ = b, unde 0 < b − a < 2π. Atunci, aria lui R este

Acest rezultat poate fi găsit după cum urmează. Întâi, intervalul [a, b] este divizat în n subintervale, unde n este un întreg pozitiv arbitrar. Astfel Δθ, lungimea fiecărui subinterval, este egală cu b − a (lungimea totală a intervalului), împărțită la n, numărul de subintervale. Pentru fiecare subinterval i = 1, 2, …, n, fie θi mijlocul fiecărui subinterval. Se construiește un sector cu centrul în pol, raza r(θi), și unghiul la centru Δθ. Aria fiecărui sector construit este deci egală cu . Deci, aria totală a tuturor sectoarelor însumate este
Cu creșterea numărului de subintervale n, aproximarea ariei continuă să se îmbunătățească. La limită, când n → ∞, suma devine suma Riemann a integralei de mai sus.
Generalizare[modificare | modificare sursă]
Folosind coordonate carteziene, un element de arie infinitezimal poate fi calculat ca dA = dx dy. Regula de substituție pentru integralele multiple afirmă că, la folosirea altor coordonate, trebuie să fie considerat determinantul Jacobian al formulei de conversie de coordonate:
Astfel un element de arie în coordonate polare poate fi scris sub forma
Acum, o funcție dată în coordonate polare poate fi integrată după cum urmează:
Aici, R este aceeași regiune ca și mai sus, și anume regiunea cuprinsă între o curbă r(θ) și razele θ = a și θ = b.
Formula pentru aria lui R menționat mai sus este obținută luând f identic egal cu 1. O aplicație surprinzătoare a acestui rezultat furnizează integrala gaussiană
Analiza vectorială[modificare | modificare sursă]
Calculul vectorial poate fi și el aplicat în coordonate polare. Fie vectorul poziție , cu r și funcții de timpul t, versorul în direcția și vector unitate în unghi drept cu . Primele derivate ale poziției sunt
Trei dimensiuni[modificare | modificare sursă]
Sistemul de coordonate polare este extins în trei dimensiuni la două sisteme de coordonate diferite: sistemul de coordonate sferice și cel de coordonate cilindrice; ambele având sistemul de coordonate polare în plan ca subset. În esență, sistemul de coordonate cilindrice extinde coordonatele polare adăugând o coordonată de distanță adițională, iar sistemul sferic mai introduce o coordonată unghiulară.
Coordonate cilindrice[modificare | modificare sursă]
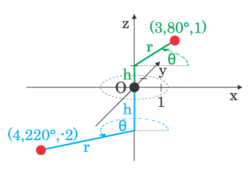
Sistemul de coordonate cilindrice este un sistem de coordonate care extinde sistemul de coordonate polare în două dimensiuni prin adăugarea unei a treia coordonate care măsoară distanța între un punct și plan, similar cu felul în care sistemul de coordonate carteziene este extins în trei dimensiuni. A treia coordonată este de obicei notată cu h, rezultând cele trei coordonate cilindrice (r, θ, h).
Cele trei coordonate cilindrice pot fi convertite în coordonate carteziene prin transformarea:
Coordonate sferice[modificare | modificare sursă]

Coordonatele polare pot fi extinse în trei dimensiuni folosind și coordonatele (ρ, φ, θ), unde ρ este distanța de la origine, φ este unghiul făcut cu axa z (numită colatitudine sau zenit și măsurată de la 0 la 180°) iar θ este unghiul cu axa x (ca și în coordonate polare). Acest sistem de coordonate, numit sistemul de coordonate sferice, este similar cu sistemul de latitudine și longitudine folosit pentru Pământ, cu originea în centrul Pământului, latitudinea δ fiind complementul lui φ, determinat de relația δ = 90° − φ, iar longitudinea l fiind măsurată ca l = θ − 180°.[17]
Cele trei coordonate sferice pot fi convertite în coordonate carteziene prin transformarea:
Aplicații[modificare | modificare sursă]
Coordonatele polare sunt bidimensionale și deci pot fi folosite doar acolo unde locațiile punctelor se află într-un plan bidimensional. Sunt folosite în orice context în care fenomenul luat în considerare este inerent legat de direcția și distanța de un punct central. De exemplu, ecuații polare elementare sunt suficiente pentru a defini unele curbe – astfel este spirala lui Arhimede – a cărei ecuație în coordonate carteziene ar fi mai complexă. Mai mult, multe sisteme fizice – cum ar fi cele ce tratează corpuri în mișcare în jurul unui punct central sau cu fenomene ce își au originea dintr-un punct central – sunt mai simplu și mai intuitiv de modelat în coordonate polare. Motivația inițială pentru introducerea sistemului polar a fost studiul mișcării circulare și orbitale.
[modificare | modificare sursă]
Coordonatele polare sunt folosite adesea în navigație, întrucât destinația sau direcția deplasării pot fi date ca unghiul și distanța de la obiectul luat în considerație. De exemplu, avioanele folosesc o versiune ușor modificată a coordonatelor polare la navigație. În acest sistem, cel folosit în general pentru orice fel de navigație, raza de 0° este în general numită direcția 360, iar unghiurile continuă în sens orar, și nu trigonometric, ca în sistemele matematice. Direcția 360 corespunde nordului magnetic, iar direcțiile 90, 180, și 270 corespund estului magnetic, sudului, și vestului, respectiv.[18]
Modelare[modificare | modificare sursă]

Sistemele care prezintă simetrie radială furnizează contexte naturale pentru sistemele de coordonate polare, cu centrul de simetrie comportându-se ca pol. Un prim exemplu de astfel de sistem este ecuația de curgere a apelor subterane aplicată puțurilor cu simetrie radială. Sistemele cu o forță radială sunt și ele bune candidate pentru utilizarea sistemului de coordonate polare. Aceste sisteme includ câmpuri gravitaționale, care respectă legea invers pătratică, precum și sisteme cu surse punctiforme, cum ar fi antenele radio.
Și sistemele radial asimetrice pot fi modelate în coordonate polare. De exemplu, răspunsul proporțional al unui microfon la un sunet exterior poate fi reprezentat prin curbe polare. Curba unui microfon cardioid standard, cel mai comun microfon direcțional, poate fi reprezentată de ecuația r = 0.5 + 0.5 sin θ.[19]
Modelarea tridimensională a disipării puterii date de boxe se poate utiliza pentru a le prezice comportamentul. Sunt necesare mai multe grafice polare, la o gamă largă de frecvențe, șablonul de distribuție a energiei variind puternic cu frecvența. Graficele polare arată că multe boxe tind spre omnidirecționalitate la frecvențe joase.
Note[modificare | modificare sursă]
- ^ a b Brown, Richard G. (). Andrew M. Gleason, ed. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. Evanston, Illinois: McDougal Littell. ISBN 0-395-77114-5.
- ^ Friendly, Michael. „Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization”. Accesat în .
- ^ King, David A. (). „The Sacred Geography of Islam”. În Koetsier, Teun; Luc, Bergmans. Mathematics and the Divine: A Historical Study. Amsterdam: Elsevier. pp. 162–78. ISBN 0-444-50328-5.
- ^ King (2005, p. 169). Calculele erau atât de precise cât se putea în condițiile limitărilor impuse de presupunerea că Pământul este o sferă perfectă.
- ^ a b Coolidge, Julian (). „The Origin of Polar Coordinates”. American Mathematical Monthly. 59: 78–85.
- ^ Boyer, C. B. (). „Newton as an Originator of Polar Coordinates”. American Mathematical Monthly. 56: 73–78.
- ^ „Math93.com”. Arhivat din original la . Accesat în .
- ^ „Polar Coordinates and Graphing” (PDF). 2006-04-13. Arhivat din original (PDF) la 2012-02-09. Accesat în 2006-09-22. Verificați datele pentru:
|date=(ajutor) - ^ Lee, Theodore (). Precalculus: With Unit-Circle Trigonometry (ed. Fourth Edition). Thomson Brooks/Cole. ISBN 0534402305.
- ^ Stewart, Ian (). Complex Analysis (the Hitchhiker's Guide to the Plane). Cambridge University Press. ISBN 0521287634.
- ^ Serway, Raymond A. (). Principles of Physics. Brooks/Cole—Thomson Learning. ISBN 0-534-49143-X.
- ^ Torrence, Bruce Follett (). The Student's Introduction to Mathematica®. Cambridge University Press. ISBN 0521594618.
- ^ Claeys, Johan. „Polar coordinates”. Arhivat din original la . Accesat în .
- ^ Smith, Julius O. (). „Euler's Identity”. Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. ISBN 0-9745607-0-7. Arhivat din original la . Accesat în .
- ^ Husch, Lawrence S. „Areas Bounded by Polar Curves”. Arhivat din original la . Accesat în .
- ^ Lawrence S. Husch. „Tangent Lines to Polar Graphs”. Arhivat din original la . Accesat în .
- ^ Wattenberg, Frank (). „Spherical Coordinates”. Arhivat din original la . Accesat în .
- ^ Santhi, Sumrit. „Aircraft Navigation System”. Accesat în .
- ^ Eargle, John (). Handbook of Recording Engineering (ed. Fourth Edition). Springer. ISBN 0387284702.
Bibliografie[modificare | modificare sursă]
- en Adams, Robert; Christopher Essex (). Calculus: a complete course (în engleză) (ed. Eighth). Pearson Canada Inc. ISBN 978-0-321-78107-9.
- en Anton, Howard; Irl Bivens; Stephen Davis (). Calculus (în engleză) (ed. Seventh Edition). Anton Textbooks, Inc. ISBN 0-471-38157-8.
- en Finney, Ross; George Thomas; Franklin Demana; Bert Waits (). Calculus: Graphical, Numerical, Algebraic (în engleză) (ed. Single Variable Version). Addison-Wesley Publishing Co. ISBN 0-201-55478-X.
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
- en FooPlot (online function plotter in polar coordinates) Arhivat în , la Wayback Machine.
- en Online conversion tool between polar and Cartesian coordinates
















































