Snub

Cub snub sau
Cuboctaedru snub

Dodecaedru snub sau
Icosidodecaedru snub

În geometrie, snub este o operație aplicată unui poliedru. Termenul provine din numele date de Kepler la două poliedre arhimedice: cubul snub (cubus simus) și dodecaedrul snub (dodecaedron simum).^[1] În general, snuburile au simetrie chirală cu două forme: cu orientare în sensul acelor de ceasornic sau în sens invers acelor de ceasornic. După numele lui Kepler, un snub poate fi văzut ca o expandare a unui poliedru regulat: deplasarea fețelor, răsucirea lor în jurul centrelor lor, adăugarea de poligoane noi centrate pe vârfurile originale și adăugarea de perechi de triunghiuri care se încadrează între marginile originale.

Terminologia a fost generalizată de Coxeter, cu o definiție ușor diferită, pentru o gamă mai largă de politopuri uniforme.

Snubul Conway

John Conway a explorat operatorii poliedrici generalizați, definind ceea ce acum se numește acum notația Conway a poliedrelor, care poate fi aplicată poliedrelor și pavărilor. Conway numește operația așa cum a fost definită de Coxeter semisnub.

În această notație, operatorul snub (s) este definit de operatorii dual (d) și giro (g) drept s = dg și este echivalent cu o alternare a unei trunchieri a operatorului ambo. Notația Conway evită operația de alternare (half) a lui Coxeter, deoarece se aplică numai la poliedre cu fețe poligonale cu un număr par de laturi.

Figuri regulate snub
Forme pentru snub	Poliedre			Pavări euclidiene		Pavări hiperbolice
Nume	Tetraedru	Cub or octaedru	Icosaedru sau dodecaedru	Pavare pătrată	Pavare hexagonală sau Pavare triunghiulară	Pavare heptagonală sau Pavare triunghiulară de ordinul 7
Imagini
Notația Conway	sT	sC = sO	sI = sD	sQ	sH = sΔ	sΔ₇
Imagini

În 4 dimensiuni Conway propune că 24-celule snub ar trebui numit 24-celule semisnub, deoarece, spre deosebire de poliedrele snub tridimensionale, sunt forme omnitrunchiate alternate, nu este un 24-celule omnitrunchiat alternat. În schimb, este de fapt un 24-celule trunchiat alternat.^[2]

Snubul Coxeter, regulat și cvasiregulat

Un cub snub poate fi construit dintr-un rombicuboctaedru prin rotirea celor 6 fețe pătrate albastre până când cele 12 fețe pătrate albe devin perechi de fețe triunghiulare echilaterale

Terminologia lui Coxeter este ușor diferită, înseamnând o trunchiere alternată, obținâmd cubul snub ca un cuboctaedru snub, iar dodecaedrul snub ca un icosidodecaedru snub. Această definiție este utilizată în denumirile a două poliedre Johnson: bisfenoidul snub și antiprisma pătrată snub, precum și în politopuri din dimensiuni superioare, cum ar fi 4-dimensionalul 24-celule snub, cu simbolul Schläfli extins s{3,4,3} și diagrama Coxeter .

Un poliedru regulat (sau pavare), cu simbolul Schläfli ${\begin{Bmatrix}p,q\end{Bmatrix}}$ , și diagrama Coxeter are trunchierea definită ca $t{\begin{Bmatrix}p,q\end{Bmatrix}}$ și , și are snubul definit ca trunchierea alternată $ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}$ și . Această construcție alternată necesită ca q să fie par.

Un poliedru cvasiregulat, cu simbolul Schläfli ${\begin{Bmatrix}p\\q\end{Bmatrix}}$ sau r{p,q} și diagrama Coxeter sau , are trunchierea cvasiregulată definită ca $t{\begin{Bmatrix}p\\q\end{Bmatrix}}$ sau tr{p,q} și sau și are snubul cvasiregulat definit ca rectificarea trunchiată alternată $ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}$ or htr{p,q} = sr{p,q} și sau .

Cub snub, obținut din cub sau cuboctaedru
Nume	Cub	Cuboctaedru Cub rectificat	Cuboctaedru trunchiat Cub cantitrunchiat	Cuboctaedru snub Cub rectificat snub
	Sămânță	Rectificat r	Trunchiat t	Alternat h
Notația Conway	C	CO rC	tCO trC or trO	htCO = sCO htrC = srC
Simbol Schläfli	{4,3}	${\begin{Bmatrix}4\\3\end{Bmatrix}}$ or r{4,3}	$t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ or tr{4,3}	$ht{\begin{Bmatrix}4\\3\end{Bmatrix}}=s{\begin{Bmatrix}4\\3\end{Bmatrix}}$ htr{4,3} = sr{4,3}
Diagramă Coxeter		sau	sau	sau
Imagine

De exemplu, cubul snub al lui Kepler este obținut din cuboctaedrul cvasiregulat, cu un simbol Schläfli vertical ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ și diagrama Coxeter , iar așa este mai explicit numit cuboctaedru snub, exprimat de un simbol Schläfli vertical $s{\begin{Bmatrix}4\\3\end{Bmatrix}}$ și o diagramă Coxeter . Cuboctaedrul snub este alternarea cuboctaedrului trunchiat, $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ și .

Poliedrele regulate cu fețe cu un număr par de vârfuri pot fi, de asemenea, snubate ca trunchieri alternate, cum ar fi octaedru snub, așa cum $s{\begin{Bmatrix}3,4\end{Bmatrix}}$ , , este alternarea octaedrului trunchiat, $t{\begin{Bmatrix}3,4\end{Bmatrix}}$ și .. Octaedru snub reprezintă pseudoicosaedrul, un icosaedru regulat cu simetrie piritoedrică.

Tetratetraedrul snub, ca $s{\begin{Bmatrix}3\\3\end{Bmatrix}}$ și , este alternarea formei cu simetrie tetraedică, trunchiate, $t{\begin{Bmatrix}3\\3\end{Bmatrix}}$ și .

Nume	Octaedru	Octaedru trunchiat	Octaedru snub
	Sămânță	Trunchiat t	Alternat h
Notația Conway	O	tO	htO or sO
Simbol Schläfli	{3,4}	t{3,4}	ht{3,4} = s{3,4}
Diagramă Coxeter
Imagine

Operația snub definită de Coxeter permite să se definească n-antiprismele ca $s{\begin{Bmatrix}2\\n\end{Bmatrix}}$ sau $s{\begin{Bmatrix}2,2n\end{Bmatrix}}$ , bazate pe n-prismele $t{\begin{Bmatrix}2\\n\end{Bmatrix}}$ or $t{\begin{Bmatrix}2,2n\end{Bmatrix}}$ , unde ${\begin{Bmatrix}2,n\end{Bmatrix}}$ este un n-hosoedru regulat, un poliedru degenerat, dar o pavare validă a sferei cu fețe în formă de digoane sau lentile.

Hosoedre snub, {2,2p}
Imagine
Diagrame Coxeter							... ...
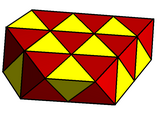
SimboluriSchläfli	s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,12}	s{2,14}	s{2,16}...	s{2,∞}
SimboluriSchläfli	sr{2,2} $s{\begin{Bmatrix}2\\2\end{Bmatrix}}$	sr{2,3} $s{\begin{Bmatrix}2\\3\end{Bmatrix}}$	sr{2,4} $s{\begin{Bmatrix}2\\4\end{Bmatrix}}$	sr{2,5} $s{\begin{Bmatrix}2\\5\end{Bmatrix}}$	sr{2,6} $s{\begin{Bmatrix}2\\6\end{Bmatrix}}$	sr{2,7} $s{\begin{Bmatrix}2\\7\end{Bmatrix}}$	sr{2,8}... $s{\begin{Bmatrix}2\\8\end{Bmatrix}}$ ...	sr{2,∞} $s{\begin{Bmatrix}2\\\infty \end{Bmatrix}}$
Notația Conway	A2 = T	A3 = O	A4	A5	A6	A7	A8...	A∞

Același proces se aplică pavărilor snub:

Pavare triunghiulară Δ	Pavare triunghiulară trunchiată tΔ	Pavare triunghiulară snub htΔ = sΔ
{3,6}	t{3,6}	ht{3,6} = s{3,6}

Exemple

Snuburi bazate pe {p,4}
Spațiu	Sferic		Euclidian	Hiperbolic
Imagine
Diagramă Coxeter								...
Simbol Schläfli	s{2,4}	s{3,4}	s{4,4}	s{5,4}	s{6,4}	s{7,4}	s{8,4}	s{∞,4}

Snuburi cvasiregulate bazate pe r{p,3}
Notația Conway	Sferic				Euclidian	Hiperbolic
Imagine
Diagramă Coxeter								...
Simbol Schläfli	sr{2,3}	sr{3,3}	sr{4,3}	sr{5,3}	sr{6,3}	sr{7,3}	sr{8,3}	... sr{∞,3}
Simbol Schläfli	$s{\begin{Bmatrix}2\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}3\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}4\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}5\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}6\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}7\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}8\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}\infty \\3\end{Bmatrix}}$
Notație Conway	A3	sT	sC sau sO	sD sau sI	sΗ sau sΔ

Snuburi cvasiregulate bazate pe r{p,4}
Spațiu	Sferic		Euclidian	Hiperbolic
Imagine
Diagramă Coxeter								...
Simbol Schläfli	sr{2,4}	sr{3,4}	sr{4,4}	sr{5,4}	sr{6,4}	sr{7,4}	sr{8,4}	...sr{∞,4}
Simbol Schläfli	$s{\begin{Bmatrix}2\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}3\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}4\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}5\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}6\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}7\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}8\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}\infty \\4\end{Bmatrix}}$
Notația Conway	A4	sC sau sO	sQ

Poliedre neuniforme snub

Poliedrele neuniforme cu toate fețele având un număr par de vârfuri pot fi snubate, inclusiv unele seturi infinite; de exemplu:

Bipiramide snub sdt{2,p}
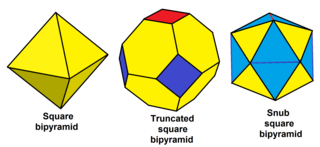
Bipiramidă pătrată snub


Bipiramidă hexagonală snub

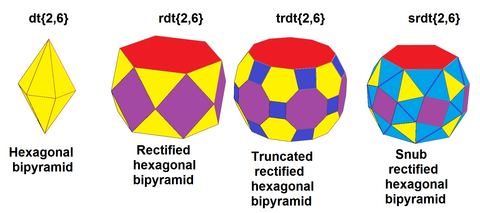
Bipiramide rectificate snub srdt{2,p}

Antiprisme snub s{2,2p}
Imagine				...
Simbol Schläfli	ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}...
Simbol Schläfli	ssr{2,2} $ss{\begin{Bmatrix}2\\2\end{Bmatrix}}$	ssr{2,3} $ss{\begin{Bmatrix}2\\3\end{Bmatrix}}$	ssr{2,4} $ss{\begin{Bmatrix}2\\4\end{Bmatrix}}$	ssr{2,5}... $ss{\begin{Bmatrix}2\\5\end{Bmatrix}}$

Poliedrele stelate uniforme snub (Coxeter)

Poliedrele stelate snub se construiesc pe baza triunghiurilor Schwarz (p q r), cu unghiurile reflexiilor ordonate rațional, iar toate oglinzile sunt active și alternate.

Poliedre stelate uniforme snub
s{3/2,3/2}	s{(3,3,5/2)}	sr{5,5/2}	s{(3,5,5/3)}	sr{5/2,3}
sr{5/3,5}	s{(5/2,5/3,3)}	sr{5/3,3}	s{(3/2,3/2,5/2)}	s{3/2,5/3}

Politopuri și faguri snub din dimensiuni superioare (Coxeter)

În general, un 4-politop regulat cu simbolul Schläfli ${\begin{Bmatrix}p,q,r\end{Bmatrix}}$ , și diagrama Coxeter , are snubul cu simbolul Schläfli extins $s{\begin{Bmatrix}p,q,r\end{Bmatrix}}$ și .

Un 4-politop rectificat ${\begin{Bmatrix}p\\q,r\end{Bmatrix}}$ = r{p,q,r}, și are simbolul snubului $s{\begin{Bmatrix}p\\q,r\end{Bmatrix}}$ = sr{p,q,r} și .

Exemple

Există un singur 4-politop convex uniform snub, 24-celule snub. 24-celule regulat are simbolul Schläfli ${\begin{Bmatrix}3,4,3\end{Bmatrix}}$ și diagrama Coxeter , iar 24-celule snub este reprezentat de $s{\begin{Bmatrix}3,4,3\end{Bmatrix}}$ și diagrama Coxeter diagram . El are și o construcție cu o simetrie indice 6 ca $s\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}$ sau s{3^1,1,1} și , și o subsimetrie indice 3 ca $s{\begin{Bmatrix}3\\3,4\end{Bmatrix}}$ sau sr{3,3,4} și sau .

Fagurele 24-celule snub asociat poate fi văzut ca $s{\begin{Bmatrix}3,4,3,3\end{Bmatrix}}$ sau s{3,4,3,3} și , iar cu simetrie mai mică $s{\begin{Bmatrix}3\\3,4,3\end{Bmatrix}}$ sau sr{3,3,4,3} și sau , iar cu o formă cu simetrie mai mică ca $s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}$ sau s{3^1,1,1,1} și .

Un fagure euclidian este un fagurele sleb hexagonal alternat, s{2,6,3} și sau sr{2,3,6} și sau sr{2,3^[3]} și .

Alt fagure euclidian (scaliform) este fagurele sleb pătrat alternat, s{2,4,4} și sau sr{2,4^1,1} și :

Unicul fagure uniform hiperbolic snub este fagurele pavare hexagonală snub, ca s{3,6,3} și , care poate fi construit și ca un fagure pavare hexagonală alternată, h{6,3,3}, . El poate fi construit și ca s{3^[3,3]} și .

Alt fagure hiperbolic (scaliform) este fagurele octaedric snub de ordinul 4, s{3,4,4} și .

Note

^ la Kepler, Harmonices Mundi, 1619
^ Conway, 2008, p. 401 Gosset's Semi-snob Polyoctahedron

Bibliografie

en Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). „Uniform polyhedra”. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. The Royal Society. 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446.
en Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8 (pp. 154–156 8.6 Partial truncation, or alternation)
en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6 [1], Googlebooks [2]
- (Paper 17) H.S.M. Coxeter, The Evolution of Coxeter–Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233–248]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
en H.S.M. Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN: 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
en Norman Johnson Uniform Polytopes, Manuscript (1991)
en N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5
en Eric W. Weisstein, Snubification la MathWorld.
en Richard Klitzing, Snubs, alternated facetings, and Stott–Coxeter–Dynkin diagrams, Symmetry: Culture and Science, Vol. 21, No.4, 329–344, (2010) [3]

v • d • m Operatori poliedrici
Sămânță	Trunchiere	Rectificare	Bitrunchiere	Dual	Expandare	Omnitrunchiere	Alternări


t₀{p,q} {p,q}	t₀₁{p,q} t{p,q}	t₁{p,q} r{p,q}	t₁₂{p,q} 2t{p,q}	t₂{p,q} 2r{p,q}	t₀₂{p,q} rr{p,q}	t₀₁₂{p,q} tr{p,q}	ht₀{p,q} h{q,p}	ht₁₂{p,q} s{q,p}	ht₀₁₂{p,q} sr{p,q}

[1] Kepler, Harmonices Mundi, 1619

[2] Conway, 2008, p. 401 Gosset's Semi-snob Polyoctahedron

[1]

[2]