Coordonate generalizate (fizică)

Parte a seriei de articole despre
Mecanică clasică
${\vec {F}}=m{\vec {a}}$ Principiul al II-lea al mecanicii
Istorie Cronologie
Ramuri Cinematică Dinamică Mecanică cerească aplicată a mediilor continue statistică Statică
Concepte Accelerație Energie cinetică potențială Forță aparentă frecare Impuls Inerție Lucru mecanic virtual Masă Moment cinetic de inerție Principiul lui D'Alembert Putere Sistem de referință inerțial neinerțial Spațiu Timp Viteză relativă
Formulări Legile lui Newton Mecanică analitică Mecanică lagrangiană Mecanică hamiltoniană Ecuația Hamilton–Jacobi
Subiecte de bază Deplasare Legea atracției universale Mișcare ecuații armonică rectilinie Solid rigid
Rotație Rotație Sistem de referință în rotație Viteză unghiulară Accelerație unghiulară Forță centripetă centrifugă Forța Coriolis Frecvență Oscilație oscilator armonic amortizare Pendul conic Vibrație
Oameni de știință Galileo Huygens Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
Categorii Mecanică clasică

În mecanica analitică, coordonatele generalizate constituie un set de parametri care sunt utilizați pentru a descrie configurația unui sistem într-un spațiu de configurație. Acești parametri ar trebui să definească în mod unic configurația sistemului în comparație cu o stare de referință. Vitezele generalizate corespund derivatelor în timp ale coordonatelor generalizate ale sistemului. Adjectivul „generalizat” distinge acești parametri de utilizarea tradițională a termenului „coordonată”, care se referă la coordonatele carteziene.

Un exemplu de coordonată generalizată ar putea fi descrierea poziției unui pendul prin unghiul pe care pendulul îl formează cu verticala, în loc de pozițiile x și y ale bobului pendulului.

Deși pot exista numeroase opțiuni pentru coordonatele generalizate ale unui sistem fizic, acestea sunt de obicei alese pentru a simplifica calculele, cum ar fi rezolvarea ecuațiilor de mișcare ale sistemului. Dacă coordonatele sunt independente una de cealaltă, numărul de coordonate generalizate independente este definit de numărul de grade de libertate ale sistemului.

Coordonatele generalizate sunt asociate cu momentele generalizate pentru a furniza coordonate canonice în spațiul fazelor.

Constrângeri și grade de libertate

Coordonatele generalizate sunt adesea selectate pentru a furniza numărul minim de coordonate independente care definesc configurația unui sistem. Aceasta simplifică formularea ecuațiilor de mișcare ale lui Lagrange. Cu toate acestea, este posibil ca un set util de coordonate generalizate să fie dependent, ceea ce implică faptul că sunt legate de una sau mai multe ecuații de constrângere.

Constrângeri holonomice

O coordonată generalizată (un grad de libertate) pe curbe în 2D. Este suficientă o singură coordonată generalizată pentru a specifica în mod unic poziția pe o curbă în 2D. În exemplele prezentate, această variabilă poate fi fie lungimea arcului s, fie unghiul θ. Nu este necesară deținerea ambelor coordonate carteziene (x și y), deoarece una dintre ele poate fi determinată din cealaltă folosind ecuațiile curbei. Ambele coordonate pot fi, de asemenea, parametrizate prin s sau θ.

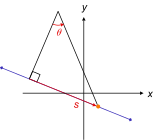
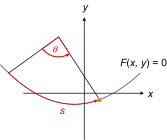
Lungimea arcului s de-a lungul curbei reprezintă o coordonată generalizată validă, deoarece determină în mod unic poziția pe curbă. În schimb, unghiul θ nu este o coordonată generalizată validă, deoarece există mai multe poziții posibile pentru o singură valoare a lui θ.

Pentru un sistem de N particule în spațiul de coordonate reale 3D, vectorul de poziție al fiecărei particule poate fi exprimat ca un tuplu de 3 elemente în coordonate carteziene:

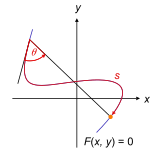
Traiectorie cu curbă deschisă F(x, y) = 0. Raza poate avea mai multe puncte de intersecție cu traiectoria.

Traiectorie cu curbă închisă C(x, y) = 0. Traiectoria poate avea puncte de intersecție cu ea însăși.

${\begin{aligned}&\mathbf {r} _{1}=(x_{1},y_{1},z_{1}),\\&\mathbf {r} _{2}=(x_{2},y_{2},z_{2}),\\&\qquad \qquad \vdots \\&\mathbf {r} _{N}=(x_{N},y_{N},z_{N})\end{aligned}}$

Oricare dintre vectorii de poziție poate fi notat ca r_k, unde k = 1, 2, …, N etichetează particulele. O constrângere holonomică reprezintă o ecuație de constrângere specifică pentru particula k

$f(\mathbf {r} _{k},t)=0$

care leagă toate cele trei coordonate spațiale ale unei particule, făcându-le interdependente. Constrângerea poate varia în timp, astfel încât variabila timp t va apărea explicit în ecuațiile de constrângere. În orice moment, o coordonată poate fi determinată din celelalte. De exemplu, dacă sunt cunoscute x_k și z_k, atunci și y_k poate fi determinată. O ecuație de constrângere corespunde unei singure constrângeri. Dacă există C constrângeri, fiecare dintre ele are o ecuație, rezultând un total de C ecuații de constrângere. Nu este necesar ca fiecare particulă să aibă o ecuație de constrângere specifică. Un sistem fără constrângeri nu are ecuații de constrângere.

Două coordonate generalizate (două grade de libertate) pe suprafețe curbe în 3D. Sunt necesare doar două numere, (u și v), pentru a specifica în mod unic punctele de pe curbă. O posibilitate pentru fiecare caz este prezentată mai jos. Cele trei coordonate carteziene (x, y și z) , nu sunt necesare, deoarece oricare două dintre ele pot determina a treia folosind ecuațiile curbei. De asemenea, pot fi parametrizate prin (u sau v).

Până acum, configurația sistemului este definită de 3N mărimi, dar pot fi eliminate C coordonate, câte una pentru fiecare ecuație de constrângere. Numărul de coordonate independente este n = 3N − C . (În spații dimensionale D, configurația originală ar necesita ND coordonate, iar reducerea prin constrângeri ar rezulta în n = ND − C). Este ideal să se utilizeze numărul minim de coordonate necesare pentru a defini configurația întregului sistem, beneficiind în același timp de constrângerile impuse acestuia. Aceste mărimi sunt cunoscute sub numele de coordonate generalizate în acest context și sunt notate ca q_j(t). Este convenabil să fie colectate într-un tuplu n.

$\mathbf {q} (t)=(q_{1}(t),\ q_{2}(t),\ \ldots ,\ q_{n}(t))$

care reprezintă un punct din spațiul de configurare al sistemului. Ele sunt independente una de cealaltă și pot fi funcții ale timpului. Din punct de vedere geometric, acestea pot reprezenta lungimi de-a lungul liniilor drepte, lungimi de arc de-a lungul curbelor sau unghiuri, nu neapărat coordonate carteziene sau alte sisteme de coordonate ortogonale standard. Numărul de coordonate generalizate este egal cu numărul de grade de libertate ale sistemului. Un grad de libertate corespunde unei mărimi care poate modifica configurația sistemului, de exemplu unghiul unui pendul sau lungimea arcului parcurs de o mărgică pe un fir.

Alegerea coordonatelor generalizate este crucială pentru simplificarea ecuațiilor de mișcare ale sistemului. Dacă, din constrângerile sistemului, se pot identifica un număr de variabile independente egal cu numărul de grade de libertate, acestea pot fi utilizate ca coordonate generalizate. Vectorul de poziție r_k al particulei k este o funcție a tuturor celor n coordonate generalizate (și, prin urmare, a timpului),

$\mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} (t))\,,$

iar coordonatele generalizate pot fi interpretate ca parametri asociați cu constrângerea.

Derivatele în timp ale coordonatelor generalizate q sunt numite viteze generalizate,

${\dot {\mathbf {q} }}={\frac {d\mathbf {q} }{dt}}=({\dot {q}}_{1}(t),\ {\dot {q}}_{2}(t),\ \ldots ,\ {\dot {q}}_{n}(t))$

(fiecare punct deasupra unei cantități indică o singură derivată în timp). Vectorul viteză v_k al particulei $k$ este derivata totală a vectorului de poziție r_k în raport cu timpul

$\mathbf {v} _{k}={\dot {\mathbf {r} }}_{k}={\frac {d\mathbf {r} _{k}}{dt}}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}\,.$

și, prin urmare, depinde atât de vitezele generalizate, cât și de coordonatele generalizate. Având libertatea de a specifica valorile inițiale ale coordonatelor generalizate și ale vitezelor generalizate separat, coordonatele generalizate q_j și vitezele generalizate dq_j/dt pot fi considerate variabile independente.

Constrângeri neholonomice

Un sistem mecanic poate avea constrângeri atât asupra coordonatelor generalizate, cât și asupra derivatelor acestora. Constrângerile de acest tip sunt denumite constrângeri neholonomice. Constrângerile neholonomice de ordinul întâi pot fi exprimate sub forma:

$g(\mathbf {q} ,{\dot {\mathbf {q} }},t)=0\,,$

Un exemplu de constrângere neholonomică de ordinul întâi este o roată care se rostogolește pe o suprafață plană. Restricția impusă de suprafața plană este că punctul de contact dintre roată și suprafață nu poate să se deplaseze vertical. Constrângerile neholonomice pot implica și derivate de ordin superior, cum ar fi accelerațiile generalizate. De exemplu, o constrângere neholonomică de ordinul al doilea ar putea limita viteza de rotație a unei roți.

Mărimi fizice în coordonate generalizate

Energie cinetică

Energia cinetică totală a sistemului mecanic reprezintă energia sa de mișcare și este definită ca:

$T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}{\dot {\mathbf {r} }}_{k}\cdot {\dot {\mathbf {r} }}_{k}\,,$

în care · este produsul scalar. Energia cinetică depinde doar de vitezele v_k și nu de coordonatele r_k în sine. Cu toate acestea, o observație importantă este:

${\dot {\mathbf {r} }}_{k}\cdot {\dot {\mathbf {r} }}_{k}=\sum _{i,j=1}^{n}\left({\frac {\partial \mathbf {r} _{k}}{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\right){\dot {q}}_{i}{\dot {q}}_{j},$

care ilustrează că energia cinetică este, în general, o funcție a vitezelor generalizate, a coordonatelor și a timpului, dacă și constrângerile variază cu timpul, deci T = T(q, dq/dt, t).

În cazul în care constrângerile asupra particulelor sunt independente de timp, toate derivatele parțiale în raport cu timpul sunt zero, iar energia cinetică devine o funcție omogenă de gradul 2 în vitezele generalizate.

Tot pentru cazul independent de timp, această expresie este echivalentă cu luarea elementului de linie la pătrat al traiectoriei particulei k,

$ds_{k}^{2}=d\mathbf {r} _{k}\cdot d\mathbf {r} _{k}=\sum _{i,j=1}^{n}\left({\frac {\partial \mathbf {r} _{k}}{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\right)dq_{i}dq_{j}\,,$

și împărțirea la diferența pătrată în timp, dt², pentru a obține viteza la pătrat a particulei k. Astfel, pentru constrângeri independente de timp, este suficient să se cunoască elementul de linie pentru a obține rapid energia cinetică a particulelor și, prin urmare, Lagrangianul.

Este instructiv să se analizeze diferitele cazuri de coordonate polare în 2D și 3D, datorită apariției lor frecvente. În coordonatele polare 2D (r, θ),

$\left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\,,$

în coordonate polare 3D (r, θ, z),

$\left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+{\dot {z}}^{2}\,,$

în coordonate sferice 3D (r, θ, φ),

$\left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2}\,.$

Momentul generalizat

Momentul generalizat conjugat canonic la coordonata q_i este definit de:

$p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.$

Dacă Lagrangianul L nu depinde de o coordonată q_i, atunci din ecuațiile Euler-Lagrange rezultă că impulsul generalizat corespunzător va fi o mărime conservată, deoarece derivata temporală este zero, ceea ce înseamnă că impulsul este o constantă a mișcării;

${\frac {\partial L}{\partial q_{i}}}={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\dot {p}}_{i}=0\,.$

Exemple

Mărgele pe un fir

Mărgea constrânsă să se deplaseze pe un fir fără frecare. Firul exercită o forță de reacție C asupra mărgelei pentru a o menține pe fir. Forța neconstrânsă N în acest caz este gravitația. De remarcat faptul că poziția inițială a firului poate duce la mișcări diferite ale mărgelei.

Pentru o mărgică care alunecă pe un fir fără frecare, supusă doar gravitației în spațiul 2D, constrângerea pe mărgică poate fi exprimată sub forma f (r) = 0 unde poziția mărgicii este r = (x(s), y(s)). Parametrul s reprezintă lungimea arcului de-a lungul curbei, pornind de la un punct de pe fir. Alegerea coordonatelor generalizate q = s este potrivită pentru sistem. Este necesară o singură coordonată în loc de două, deoarece poziția mărgelei poate fi parametrizată printr-un singur număr, s. Ecuația constrângerii leagă coordonatele x și y. Prin urmare, una dintre coordonate este determinată de cealaltă. Forța de constrângere este forța de reacție pe care firul o exercită asupra mărgelei pentru a o menține pe fir. Forța aplicată fără constrângere este gravitația care acționează asupra mărgelei.

Să presupunem că firul își schimbă forma în timp, prin îndoire. Atunci ecuația constrângerii și poziția particulei devin:

$f(\mathbf {r} ,t)=0\,,\quad \mathbf {r} =(x(s,t),y(s,t))$

Ambele depind acum de timpul t din cauza schimbării coordonatelor pe măsură ce firul își modifică forma. Timpul apare implicit prin coordonate și explicit în ecuațiile de constrângere.

Pendul simplu

Pendul simplu. Deoarece tija este rigidă, poziția bobului este constrânsă de ecuația f (x, y) = 0, forța de constrângere C este tensiunea din tijă. Din nou, forța neconstrânsă N în acest caz este gravitația.

Modelul dinamic al unui pendul simplu.

Relația dintre utilizarea coordonatelor generalizate și coordonatelor carteziene pentru caracterizarea mișcării unui sistem mecanic poate fi ilustrată prin studierea dinamicii constrânse a unui pendul simplu.

Un pendul simplu constă dintr-o masă M atârnând de un punct de pivot, fiind constrâns să se miște pe un cerc cu raza L. Poziția masei este definită de vectorul de coordonate r = (x, y) măsurat în planul cercului, unde y este pe direcția verticală. Coordonatele x și y sunt legate prin ecuația cercului:

$f(x,y)=x^{2}+y^{2}-L^{2}=0,$

care constrânge mișcarea lui M. Această ecuație oferă, de asemenea, o constrângere asupra componentelor vitezei,

${\dot {f}}(x,y)=2x{\dot {x}}+2y{\dot {y}}=0.$

Acum introducem coordonatele generalizate θ_i (i = 1, 2), care definesc poziția unghiulară a fiecărei mase a pendulului dublu față de direcția verticală. În acest caz, avem

$\mathbf {r} =(x,y)=(L\sin \theta ,-L\cos \theta ).$

Utilizarea lui θ pentru a defini configurația acestui sistem evită constrângerea oferită de ecuația cercului.

Observați că forța de gravitație care acționează asupra masei $m$ ste formulată în coordonate carteziene obișnuite,

$\mathbf {F} =(0,-mg),$

unde g este accelerația datorată gravitației.

Lucrul virtual al gravitației asupra masei m în timp ce aceasta urmează traiectoria r este dat de

$\delta W=\mathbf {F} \cdot \delta \mathbf {r} .$

Variația δr poate fi calculată în funcție de coordonatele x și y, sau în funcție de parametrul θ,

$\delta \mathbf {r} =(\delta x,\delta y)=(L\cos \theta ,L\sin \theta )\delta \theta .$

Astfel, lucrul virtual este dat de

$\delta W=-mg\delta y=-mgL\sin(\theta )\delta \theta .$

Observați că coeficientul lui δy este componenta y a forței aplicate. În același mod, coeficientul lui δθ este cunoscut ca forța generalizată de-a lungul coordonatei generalizate θ, dată de

$F_{\theta }=-mgL\sin \theta .$

Pentru a completa analiza, se consideră energia cinetică T a masei, folosind viteza,

$\mathbf {v} =({\dot {x}},{\dot {y}})=(L\cos \theta ,L\sin \theta ){\dot {\theta }},$

deci,

$T={\frac {1}{2}}m\mathbf {v} \cdot \mathbf {v} ={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2})={\frac {1}{2}}mL^{2}{\dot {\theta }}^{2}.$

Forma lui D'Alembert a principiului lucrului virtual pentru pendul în funcție de coordonatele x și y este dată de:

${\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {x}}}}-{\frac {\partial T}{\partial x}}=F_{x}+\lambda {\frac {\partial f}{\partial x}},\quad {\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {y}}}}-{\frac {\partial T}{\partial y}}=F_{y}+\lambda {\frac {\partial f}{\partial y}}.$

Astfel rezultă cele trei ecuații

$m{\ddot {x}}=\lambda (2x),\quad m{\ddot {y}}=-mg+\lambda (2y),\quad x^{2}+y^{2}-L^{2}=0,$

în cele trei necunoscute, x, y și λ.

Folosind parametrul θ, acele ecuații iau forma

${\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {\theta }}}}-{\frac {\partial T}{\partial \theta }}=F_{\theta },$

care devine,

$mL^{2}{\ddot {\theta }}=-mgL\sin \theta ,$

sau

${\ddot {\theta }}+{\frac {g}{L}}\sin \theta =0.$

Această formulare produce o singură ecuație, deoarece există un singur parametru și nicio ecuație de constrângere.

Acest lucru arată că parametrul θ este o coordonată generalizată care poate fi utilizată în același mod ca și coordonatele carteziene x și y pentru a analiza pendulul.

Pendul dublu

Un pendul dublu

Beneficiile coordonatelor generalizate devin evidente în cazul analizei unui pendul dublu. Pentru cele două mase m_i (i = 1, 2), fie r_i = (x_i, y_i), i = 1, 2, definește cele două traiectorii ale acestora. Acești vectori satisfac cele două ecuații de constrângere,

$f_{1}(x_{1},y_{1},x_{2},y_{2})=\mathbf {r} _{1}\cdot \mathbf {r} _{1}-L_{1}^{2}=0$

și

$f_{2}(x_{1},y_{1},x_{2},y_{2})=(\mathbf {r} _{2}-\mathbf {r} _{1})\cdot (\mathbf {r} _{2}-\mathbf {r} _{1})-L_{2}^{2}=0.$

Formularea ecuațiilor lui Lagrange pentru acest sistem generează șase ecuații în cele patru coordonate carteziene x_i, y_i (i = 1, 2) și cei doi multiplicatori Lagrange λ_i (i = 1, 2) care rezultă din cele două ecuații de constrângere.

Acum se introduce parametrul θ, care definește poziția unghiulară a lui $M$ față de direcția verticală. Acesta poate fi utilizat pentru a defini coordonatele $x$ și $y$, astfel încât

$\mathbf {r} _{1}=(L_{1}\sin \theta _{1},-L_{1}\cos \theta _{1}),\quad \mathbf {r} _{2}=(L_{1}\sin \theta _{1},-L_{1}\cos \theta _{1})+(L_{2}\sin \theta _{2},-L_{2}\cos \theta _{2}).$

Forța gravitației care acționează asupra maselor este dată de:

$\mathbf {F} _{1}=(0,-m_{1}g),\quad \mathbf {F} _{2}=(0,-m_{2}g)$

unde g este accelerația datorată gravitației. Prin urmare, lucrul virtual al gravitației asupra celor două mase, în timp ce acestea urmează traiectoriile r_i (i = 1, 2), este dat de formula

$\delta W=\mathbf {F} _{1}\cdot \delta \mathbf {r} _{1}+\mathbf {F} _{2}\cdot \delta \mathbf {r} _{2}.$

Variațiile δr_i (i = 1, 2) pot fi calculate ca fiind

$\delta \mathbf {r} _{1}=(L_{1}\cos \theta _{1},L_{1}\sin \theta _{1})\delta \theta _{1},\quad \delta \mathbf {r} _{2}=(L_{1}\cos \theta _{1},L_{1}\sin \theta _{1})\delta \theta _{1}+(L_{2}\cos \theta _{2},L_{2}\sin \theta _{2})\delta \theta _{2}$

Astfel, lucrul virtual este dat de

$\delta W=-(m_{1}+m_{2})gL_{1}\sin \theta _{1}\delta \theta _{1}-m_{2}gL_{2}\sin \theta _{2}\delta \theta _{2},$

iar forțele generalizate sunt

$F_{\theta _{1}}=-(m_{1}+m_{2})gL_{1}\sin \theta _{1},\quad F_{\theta _{2}}=-m_{2}gL_{2}\sin \theta _{2}.$

Calculați energia cinetică a acestui sistem ca fiind

$T={\frac {1}{2}}m_{1}\mathbf {v} _{1}\cdot \mathbf {v} _{1}+{\frac {1}{2}}m_{2}\mathbf {v} _{2}\cdot \mathbf {v} _{2}={\frac {1}{2}}(m_{1}+m_{2})L_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}L_{2}^{2}{\dot {\theta }}_{2}^{2}+m_{2}L_{1}L_{2}\cos(\theta _{2}-\theta _{1}){\dot {\theta }}_{1}{\dot {\theta }}_{2}.$

Ecuația Euler–Lagrange produce două ecuații în coordonatele generalizate necunoscute θ_i (i = 1, 2) date de

$(m_{1}+m_{2})L_{1}^{2}{\ddot {\theta }}_{1}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{2}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\dot {\theta _{2}}}^{2}\sin(\theta _{1}-\theta _{2})=-(m_{1}+m_{2})gL_{1}\sin \theta _{1},$

și

$m_{2}L_{2}^{2}{\ddot {\theta }}_{2}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{1}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\dot {\theta _{1}}}^{2}\sin(\theta _{2}-\theta _{1})=-m_{2}gL_{2}\sin \theta _{2}.$

Utilizarea coordonatelor generalizate θ_i (i = 1, 2) oferă o alternativă la formularea carteziană a dinamicii pendulului dublu.

Pendul sferic

Pendul sferic: unghiuri și viteze.

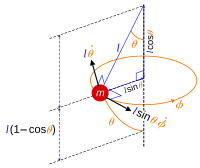
Pentru un exemplu 3D, considerăm un pendul sferic cu lungime constantă l liber să se balanseze în orice direcție unghiulară sub acțiunea gravitației, constrângerea impusă bobului pendulului poate fi exprimată sub forma

$f(\mathbf {r} )=x^{2}+y^{2}+z^{2}-l^{2}=0\,,$

unde se poate scrie poziția bobului pendulului astfel

$\mathbf {r} =(x(\theta ,\phi ),y(\theta ,\phi ),z(\theta ,\phi ))\,,$

în care (θ, φ) sunt unghiurile polare sferice polare sferice, deoarece bob-ul se mișcă pe suprafața unei sfere. Poziția r se măsoară de-a lungul punctului de suspensie până la bob, tratat aici ca o particulă punctiformă. O alegere logică a coordonatelor generalizate pentru a descrie mișcarea sunt unghiurile (θ, φ). Sunt necesare doar două coordonate în loc de trei, deoarece poziția bobului poate fi parametrizată prin două numere, iar ecuația de constrângere conectează cele trei coordonate (x, y, z), astfel încât oricare dintre ele este determinată de celelalte două.

Coordonate generalizate și lucru virtual

Principiul lucrului virtual afirmă că, dacă un sistem este în echilibru static, lucrul virtual al forțelor aplicate este zero pentru toate deplasările virtuale ale sistemului din această stare. Altfel spus, δW = 0 pentru orice variație δr. Când este formulat în termeni de coordonate generalizate, acest principiu este echivalent cu cerința ca forțele generalizate să fie zero pentru orice deplasare virtuală, deci F_i = 0.

Fie ca forțele care acționează asupra sistemului să fie notate cu F_j (j = 1, 2, …, m) și aplicate punctelor cu coordonate carteziene r_j (j = 1, 2, …, m). Atunci, lucrul virtual generat de o deplasare virtuală din poziția de echilibru este dat de:

$\delta W=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot \delta \mathbf {r} _{j}.$

unde δr_j (j = 1, 2, …, m) reprezintă deplasările virtuale ale fiecărui punct din corp.

Să presupunem acum că fiecare δr_j depinde de coordonatele generalizate q_i (i = 1, 2, …, n), atunci

$\delta \mathbf {r} _{j}={\frac {\partial \mathbf {r} _{j}}{\partial q_{1}}}\delta {q}_{1}+\ldots +{\frac {\partial \mathbf {r} _{j}}{\partial q_{n}}}\delta {q}_{n},$

și

$\delta W=\left(\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{1}}}\right)\delta {q}_{1}+\ldots +\left(\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{n}}}\right)\delta {q}_{n}.$

Cei n termeni

$F_{i}=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{i}}},\quad i=1,\ldots ,n,$

reprezintă forțele generalizate care acționează asupra sistemului. Kane arată că aceste forțe generalizate pot fi, de asemenea, formulate în termeni de raport al derivatelor în timp,

$F_{i}=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {v} _{j}}{\partial {\dot {q}}_{i}}},\quad i=1,\ldots ,n,$

unde v_j este viteza punctului de aplicare a forței F_j.

Pentru ca lucrul virtual să fie zero pentru o deplasare virtuală arbitrară, fiecare dintre forțele generalizate trebuie să fie zero, adică

$\delta W=0\quad \Rightarrow \quad F_{i}=0,i=1,\ldots ,n.$

Vezi și

• Coordonate canonice
• Mecanica hamiltoniană
• Lucrul virtual
• Coordonate ortogonale
• Coordonate curbilinii
• Matricea de masă
• Matricea de rigiditate
• Forțe generalizate

Bibliografie

• Ginsberg, Jerry H. (2008). Engineering dynamics (ed. 3rd). Cambridge UK: Cambridge University Press. ISBN 978-0-521-88303-0. 
• Goldstein, Herbert; Poole, Charles; Safko, John (2002). Classical Mechanics (ed. 3rd). San Francisco, CA: Addison Wesley. ISBN 0-201-65702-3. 
• Hand, Louis N.; Finch, Janet D. (1998). Analytical mechanics. Cambridge: Cambridge University Press. ISBN 978-0521575720. 
• Kibble, T.W.B; Berkshire, F.H. (2004). Classical Mechanics (ed. 5th). River Edge NJ: Imperial College Press. ISBN 1860944248. 
• Landau, L. D.; Lifshitz, E.M. (1976). Mechanics (ed. Third). Oxford. ISBN 978-0750628969. 
• Torby, Bruce (1984). „Energy Methods”. Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.