Hemiicosaedru

Descriere
Hemiicosaedru

Tip	poliedru abstract regulat
Fețe	10 triunghiuri
Laturi (muchii)	15
Vârfuri	6
χ	1
Configurația vârfului	3.3.3.3.3
Simbol Schläfli	{3,5}/2 sau {3,5}₅
Grup de simetrie	A₅, ordin 60
Poliedru dual	hemidodecaedru
Proprietăți	neorientabil

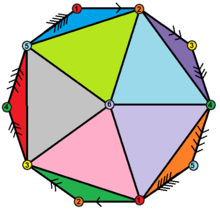
În geometrie un hemiicosaedru este un politop abstract^⁠(d) regulat, care are jumătate^[1] din fețele unui icosaedru regulat.

Realizare[modificare | modificare sursă]

Poate fi realizat ca un poliedru proiectiv^⁠(d) (o teselare a planului proiectiv real^⁠(d) cu 10 triunghiuri), care poate fi vizualizat prin construirea planului proiectiv ca o emisferă unde puncte opuse de-a lungul frontierei sunt conectate și împart emisfera în trei părți egale.

Geometrie[modificare | modificare sursă]

Are 10 fețe triunghiulare, 15 laturi și 6 vârfuri.

Este înrudit cu poliedrul uniform neconvex tetrahemihexaedru, care ar putea fi identic din punct de vedere topologic cu hemiicosaedrul dacă fiecare dintre cele 3 fețe pătrate ar fi divizată în două triunghiuri.

Grafuri[modificare | modificare sursă]

Poate fi reprezentat simetric pe fețe și vârfuri ca diagramă Schlegel.


Graf al hemiicosaedrului centrat pe o față	Diagrama Schlegel a dualului: hemidodecaedrul

Graful complet K₆[modificare | modificare sursă]

Are aceleași vârfuri și muchii ca și 5-simplexul pentadimensional, care are un graf complet al laturilor, dar conține doar jumătate din cele 20 de fețe.

Din punctul de vedere al teoriei grafurilor, aceasta este o încorporare a $K_{6}$ (graful complet cu 6 vârfuri) pe un plan proiectiv real. Cu această încorporare, graful dual^⁠(d) este graful Petersen^⁠(d) (v. hemidodecaedru).

Note[modificare | modificare sursă]

^ „hemi” la DEX online

Bibliografie[modificare | modificare sursă]

en McMullen, Peter; Schulte, Egon (decembrie 2002), „6C. Projective Regular Polytopes”, Abstract Regular Polytopes (ed. 1st), Cambridge University Press, pp. 162–165, ISBN 0-521-81496-0