Apeirogon necoliniar
În geometrie un apeirogon necoliniar sau poligon infinit necoliniar este un 2-politop infinit cu vârfuri care nu sunt toate coliniare. Apeirogoanele în zigzag sunt poligoane infinite bidimensionale cu vârfuri alternând între două drepte paralele. Apeirogoanele elicoidale sunt linii poligonale infinite tridimensionale cu vârfurile pe suprafața unui cilindru.
Apeirogoanele necoliniare regulate există în poligoanele Petrie ale grupurilor Coxeter afine și hiperbolice. Ele sunt construite cu un singur operator, care este compusul tuturor reflexiilor grupului Coxeter.
Apeirogoane regulate în zigzag în spațiul bidimensional
[modificare | modificare sursă]| Apeirogon regulat în zigzag | |
 | |
| Laturi și vârfuri | ∞ |
|---|---|
| Simbol Schläfli | {∞}#{ } |
| Grup de simetrie | D∞d, [2+,∞], (2*∞) |

Un apeirogon regulat în zigzag are simetria de friză (2*∞), D∞d.
Apeirogoanele regulate în zigzag există ca poligoane Petrie ale trei pavări regulate ale planului: {4,4}, {6,3} și {3,6}. Aceste apeirogoane regulate în zigzag au unghiurile interne de 90°, 120° și respectiv 60°, corespunzătoare poligoanelor regulate ale pavării:

|
Apeirogoane necoliniare izotoxale bidimensionale
[modificare | modificare sursă]Un apeirogon izotoxal are un singur tip de latură, între două tipuri de vârfuri alternate. Există un grad de libertate în unghiul interior, α. {∞α} este poligonul dual al unui apeirogon necoliniar izogonal.
| {∞0°} | |
| {∞30°} | 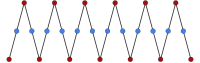
|
Apeirogoane necoliniare izogonale bidimensionale
[modificare | modificare sursă]Apeirogoane în zigzag izogonale bidimensionale
[modificare | modificare sursă]Un apeirogon necoliniar izogonal alternează două tipuri de laturi cu diverse simetrii din grupul frizei. Apeirogoanele în zigzag regulate produc apeirogoane în zigzag izogonale cu simetrie de translație:
| p1, [∞]+, (∞∞), C∞ | |
|---|---|
 
|
 
|
Apeirogoane necoliniare alungite izogonale bidimensionale
[modificare | modificare sursă]Alte apeirogoane necoliniare izogonale au laturi alternante paralele cu direcția frizei. Aceste apeirogoane alungite izogonale au simetrie verticală în oglindă față de mijloacele laturilor paralele cu direcția frizei:
| p2mg, [2+,∞], (2*∞), D∞d | ||
|---|---|---|
 |
||
Apeirogoane necoliniare alungite cvasiregulate bidimensionale
[modificare | modificare sursă]Un apeirogon necoliniar alungit izogonal are două tipuri de laturi; chiar dacă ambele tipuri de laturi au aceeași lungime, nu poate fi numit regulat deoarece cele două tipuri de laturi sunt încă diferite („latură trans” și „latură cis”), dar poate fi numit cvasiregulat.
Exemple de apeirogoane necoliniare alungite cvasiregulate pot fi văzute ca poligoane Petrie trunchiate în pavări regulate trunchiate ale planului euclidian:
Apeirogoane necoliniare hiperbolice
[modificare | modificare sursă]Apeirogoane necoliniare regulate se găsesc nu doar în planul euclidian, ci și în planul hiperbolic.
Apeirogoane necoliniare hiperbolice regulate există și ca poligoane Petrie, în zigzag între laturile pavărilor regulate ale planului hiperbolic. Și, din nou, ca și în planul euclidian, poligoanele infinite hiperbolice cvasiregulate pot fi construite ca poligoane Petrie trunchiate pe laturile pavărilor regulate trunchiate ale planului hiperbolic.
| {3,7} | t{3,7} |
|---|---|
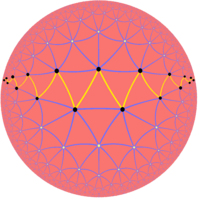 Necoliniar regulat |
 Necoliniar cvasiregulat |
Apeirogoane elicoidale
[modificare | modificare sursă]{∞} # {3} Un apeirogon elicoidal regulat (desenat în perspectivă) |
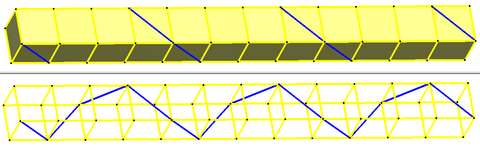
Un apeirogon (necoliniar) elicoidal poate exista în spațiul tridimensional, unde vârfurile pot fi văzute ca fiind situate pe suprafața unui cilindru. Imaginea din dreapta este o vedere în perspectivă a unui astfel de apeirogon elicoidal regulat. Acest apeirogon elicoidal poate fi văzut ca fiind construit de vârfurile unei stive infinite de prisme sau antiprisme n-gonale uniforme, deși în general unghiul de răsucire nu este limitat la un divizor întreg al 180°. Un apeirogon elicoidal are simetrie axială elicoidală.
O stivă infinită de prisme, de exemplu cuburi, conține un apeirogon elicoidal pe diagonalele fețelor pătrate, cu un unghi de răsucire de 90° și cu un simbol Schläfli {∞} # {4}.
O stivă infinită de antiprisme, de exemplu octaedre, formează apeirogoane elicoidale, 3 dintre ele sunt evidențiate cu roșu, verde și albastru, fiecare cu un unghi de răsucire de 60° și cu un simbol Schläfli {∞} # {6}.
O succesiune de laturi ale unei elice Boerdijk–Coxeter poate reprezenta apeirogoane elicoidale regulate cu un unghi de răsucire irațional:
Apeirogoane elicoidale izogonale tridimensionale
[modificare | modificare sursă]O stivă de prisme drepte poate genera apeirogoane elicoidale izogonale, care alternează laturile în jurul axei și de-a lungul axei; de exemplu, un șir de cuburi poate genera acest apeirogon elicoidal izogonal alternând laturile roșii și albastre:
Similar, o stivă alternantă de prisme și antiprisme poate produce un apeirogon elicoidal izogonal, de exemplu o stivă triunghiulară de prisme și antiprisme cu un apeirogon elicoidal izogonal:
De asemenea, un apeirogon elicoidal izogonal cu un unghi de răsucire irațional poate fi construit din tetraedre trunchiate stivuite ca o elice Boerdijk–Coxeter, alternând două tipuri de laturi, între perechi de fețe hexagonale și perechi de fețe triunghiulare:
Bibliografie
[modificare | modificare sursă]- en Coxeter, H.S.M.; Regular complex polytopes (1974). Chapter 1. Regular polygons, 1.5. Regular polygons in n dimensions, 1.7. Zigzag and antiprismatic polygons, 1.8. Helical polygons. 4.3. Flags and Orthoschemes, 11.3. Petrie polygons