Cerc circumscris

În geometrie cercul circumscris al unui poligon este un cerc care trece prin toate vârfurile poligonului.
Nu orice poligon are un cerc circumscris. Un poligon care are unul se numește poligon înscriptibil. Toate triunghiurile, poligoanele regulate, dreptunghiurile, romboizii dreptunghici și trapezele isoscele sunt înscriptibile.
O noțiune înrudită este problema cercului minim(d), care este cel mai mic cerc care conține complet poligonul în interiorul său, dacă centrul cercului se află în poligon. Fiecare poligon are un cerc minim unic, care poate fi construit printr-un algoritm liniar în timp.[1] Chiar dacă un poligon are un cerc circumscris, acesta poate fi diferit de cercul său minim. De exemplu, pentru un triunghi obtuz, cercul minim are ca diametru cea mai lungă latură și nu trece prin vârful opus.
Triunghiuri
[modificare | modificare sursă]Toate triunghiurile sunt înscriptibile, adică au cerc circumscris.
Construcție cu rigla și compasul
[modificare | modificare sursă]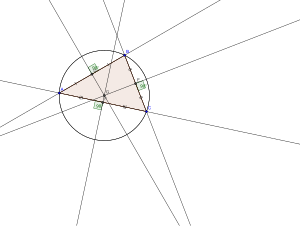
Centrul cercului circumscris unui triunghi poate fi construit trasând oricare două dintre cele trei mediatoare. Pentru trei puncte necoliniare, aceste două drepte nu pot fi paralele, iar centrul cercului circumscris este punctul în care ele se intersectează. Orice punct de pe mediatoare este echidistant de cele două capete ale laturii pe care o împarte în două, din care rezultă că acest punct, pe ambele mediatoare, este echidistant de toate cele trei vârfuri ale triunghiului. Raza cercului circumscris este distanța de la acest punct la oricare dintre cele trei vârfuri.
Ecuațiile cercului circumscris
[modificare | modificare sursă]Coordonate carteziene
[modificare | modificare sursă]În planul euclidian este posibil să se dea explicit o ecuație a cercului circumscris în funcție de coordonatele carteziene ale vârfurilor triunghiului înscris. Să presupunem că
sunt coordonatele punctelor A, B și C. Cercul circumscris este locul geometric al punctelor v = (vx, vy) din planul cartezian care satisfac ecuațiile
garantând că punctele A, B, C și v sunt la aceeași distanță r de centrul comun u al cercului. Aceste ecuații se reduc la condiția ca matricea
să aibă un nucleu diferit de zero. Astfel, cercul circumscris poate fi descris alternativ ca locul geometric al zerourilor determinantului acestei matrice:
Folosind teorema lui Laplace, fie
Se obține atunci a|v|2 − 2Sv − b = 0 unde S = (Sx, Sy), și — presupunând că cele trei puncte nu sunt coliniare (în caz contrar, cercul circumscris este acea linie care poate fi văzută și ca un cerc generalizat cu S la infinit) — |v − S/a|2 = b/a + |S|2/a2, care dă centrul cercului circumscris S/a și raza cercului circumscris √b/a + |S|2/a2. O abordare similară permite deducerea ecuației sferei circumscrise unui tetraedru.
Coordonatele centrului cercului circumscris
[modificare | modificare sursă]Coordonate carteziene
[modificare | modificare sursă]Coordonatele carteziene ale centrului cercului circumscris sunt
cu
Patrulatere înscriptibile
[modificare | modificare sursă]
Patrulaterele care pot fi circumscrise au proprietăți speciale, inclusiv faptul că unghiurile opuse sunt unghiuri suplementare (suma lor fiind 180° sau π radiani).
n-goane înscriptibile
[modificare | modificare sursă]La un poligon înscriptibil cu un număr impar de laturi toate unghiurile sunt egale dacă și numai dacă poligonul este regulat. Un poligon înscriptibil cu un număr par de laturi are toate unghiurile egale dacă și numai dacă laturile alternate sunt egale (adică laturile 1, 3, 5, ... sunt egale și laturile 2, 4, 6, ... sunt egale).[2]
În orice n-gon înscriptibil cu n par, suma unui set de unghiuri alternate (primul, al treilea, al cincilea etc.) este egală cu suma celuilalt set de unghiuri alternate. Acest lucru poate fi dovedit prin inducție din cazul n = 4, în fiecare caz înlocuind o latură cu încă trei laturi și observând că aceste trei laturi noi împreună cu latura veche formează un patrulater care are el însuși această proprietate; unghiurile alternate ale celui din urmă patrulater sunt adunate la sumele unghiurilor alternate ale n-gonului precedent.
Fie un n-gon înscris într-un cerc și un alt n-gon circumscriptibil la acel cerc. Apoi, din orice punct P al cercului, produsul distanțelor perpendiculare de la P la laturile primului n-gon este egal cu produsul distanțelor perpendiculare de la P pe laturile celui de-al doilea n-gon.[3]
Note
[modificare | modificare sursă]- ^ en Megiddo, N. (). „Linear-time algorithms for linear programming in R3 and related problems”. SIAM Journal on Computing. 12 (4): 759–776. doi:10.1137/0212052.
- ^ en De Villiers, Michael (martie 2011). „95.14 Equiangular cyclic and equilateral circumscribed polygons”. The Mathematical Gazette. 95 (532): 102–107. JSTOR 23248632.
- ^ en Johnson, Roger A. (). Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Houghton Mifflin Co. p. 72. hdl:2027/wu.89043163211. Republished by Dover Publications as Advanced Euclidean Geometry, 1960 and 2007.
Legături externe
[modificare | modificare sursă]- en Derivation of formula for radius of circumcircle of triangle la Mathalino.com
- en Semi-regular angle-gons and side-gons: respective generalizations of rectangles and rhombi lat Dynamic Geometry Sketches, cu o aplicație interactivă de geometrie dinamică.
- MathWorld
- en Eric W. Weisstein, Circumcircle la MathWorld.
- en Eric W. Weisstein, Cyclic Polygon la MathWorld.
- en Eric W. Weisstein, Steiner circumellipse la MathWorld.
- Interactive






![{\displaystyle {\begin{aligned}S_{x}&={\frac {1}{2}}\det {\begin{bmatrix}|\mathbf {A} |^{2}&A_{y}&1\\|\mathbf {B} |^{2}&B_{y}&1\\|\mathbf {C} |^{2}&C_{y}&1\end{bmatrix}},\\[5pt]S_{y}&={\frac {1}{2}}\det {\begin{bmatrix}A_{x}&|\mathbf {A} |^{2}&1\\B_{x}&|\mathbf {B} |^{2}&1\\C_{x}&|\mathbf {C} |^{2}&1\end{bmatrix}},\\[5pt]a&=\det {\begin{bmatrix}A_{x}&A_{y}&1\\B_{x}&B_{y}&1\\C_{x}&C_{y}&1\end{bmatrix}},\\[5pt]b&=\det {\begin{bmatrix}A_{x}&A_{y}&|\mathbf {A} |^{2}\\B_{x}&B_{y}&|\mathbf {B} |^{2}\\C_{x}&C_{y}&|\mathbf {C} |^{2}\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1649c42b7532a101a98ee8d0eb5f18f72a4922a1)

![{\displaystyle {\begin{aligned}U_{x}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_{y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})\right]\\[5pt]U_{y}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79248a1cfbeff74ea283e3c6c07a289fe188fb4d)
![{\displaystyle D=2\left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})\right].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34c6178eff86289b6ec6f7dd49c95d675180f944)