Momentul forței

Parte a seriei de articole despre
Mecanică clasică
${\vec {F}}=m{\vec {a}}$ Principiul al II-lea al mecanicii
Istorie Cronologie
Ramuri Cinematică Dinamică Mecanică cerească aplicată a mediilor continue statistică Statică
Concepte Accelerație Energie cinetică potențială de rotație Forță aparentă contact frecare suprafață volum Impuls Inerție Lucru mecanic virtual Masă Moment cinetic de inerție Principiul lui D'Alembert Putere Randament mecanic Sistem de referință inerțial neinerțial Spațiu Timp Viteză relativă
Formulări Legile lui Newton Mecanică analitică Mecanică lagrangiană Mecanică hamiltoniană Ecuația Hamilton–Jacobi
Subiecte de bază Deplasare Legea atracției universale Mișcare ecuații armonică rectilinie Solid rigid
Rotație Rotație Sistem de referință în rotație Viteză unghiulară Accelerație unghiulară Forță centripetă centrifugă Forța Coriolis Frecvență Oscilație oscilator armonic amortizare Pendul conic Vibrație
Oameni de știință Galileo Huygens Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
Categorii Mecanică clasică

Relația dintre forță (F) și cuplu (τ) în cazul unui corp în rotație

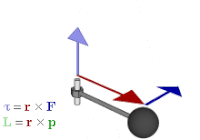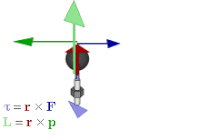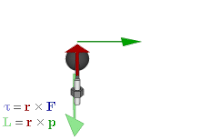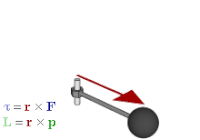
Momentul forței (sau cuplu) este o mărime fizică vectorială ce exprimă cantitativ capacitatea forței de a roti un rigid in jurul unei drepte ce trece printr-un punct și este perpendiculara pe planul format de dreapta suport a forței și punctul respectiv. Este important în funcționarea unor aparate de zbor ca de exemplu elicopterul.

Momentul unei forțe în raport cu un punct

Momentul unei forțe în raport cu un punct

Momentul forței ${\vec {F}}$ , care acționează asupra unui solid rigid ,în raport cu punctul O, numit pol, este o mărime vectorială notată cu ${\vec {M}}_{0}({\vec {F}})$ sau mai simplu notată cu ${\vec {M}}_{0}$ și reprezintă produsul vectorial dintre vectorul de poziție care unește punctul O cu un punct oarecare de pe suportul forței și forță:

${\vec {M}}_{0}={\vec {r}}\times {\vec {F}}=r\cdot F\cdot \sin(t)\cdot {\vec {u}}=F\cdot d\cdot {\vec {u}}$

unde:

$t$ este unghiul dintre ${\vec {r}}$ și ${\vec {F}}$

$d=r\cdot \sin(t)$ și este brațul forței F fața de punctul O , care reprezintă distanța de la punctul O până la dreapta suport a forței F, adică lungimea perpendicularei dusă din punctul O pe dreapta suport a forței F.

Momentul unei forțe ${\vec {F}}$ în raport cu un punct O se exprimă analitic în raport cu sistemul de referință cartezian triortogonal drept OXZY prin relația:

${\begin{aligned}{\vec {M}}_{o}({\vec {F}})&={\vec {r}}\times {\vec {F}}={\begin{bmatrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\x&y&z\\X&Y&Z\end{bmatrix}}\\&=(y\cdot Z-z\cdot Y)\cdot {\vec {i}}+(z\cdot X-x\cdot Z)\cdot {\vec {j}}+(x\cdot Y-y\cdot X)\cdot {\vec {k}}\end{aligned}}$

${\vec {M}}_{o}({\vec {F}})=M_{x}\cdot {\vec {i}}+M_{y}\cdot {\vec {j}}+M_{z}\cdot {\vec {k}}$

unde:

$M_{x}=y\cdot Z+z\cdot Y$

$M_{y}=z\cdot X-x\cdot Z$

$M_{z}=x\cdot Y-y\cdot X$

sunt proiecțiile momentului forței F in raport cu punctul O pe axele Ox , Oy si Oz

Caracteristicile vectorului moment:

• punctul de aplicație este în O, ceea ce înseamnă ca vectorul moment este un vector legat;
• direcția este normală pe planul format de O și suportul forței;
• sensul este corespunzător triedrului drept;
• mărimea (modulul) acestuia este:

$|{\vec {M}}_{0}|=|{\vec {F}}|\cdot d,$

unde d = OB se numește brațul forței și reprezinta lungimea perpendicularei dusă din O pe dreapta suport a forței.

Proprietăți

• Momentul unei forțe în raport cu un punct arbitrar de pe dreapta suport a forței este întotdeauna nul.

${\vec {M}}_{A}({\vec {F}})={\vec {AB}}\times {\vec {F}}=0$ ,deoarece ${\vec {AB}}$ si ${\vec {F}}$ sunt coliniari.

• Momentul unei forțe în raport cu un punct care nu aparține dreptei suport al forței este intotdeauna constant la alunecarea forței pe dreapta sa suport.

Demonstrație:

${\vec {M}}_{o}({\vec {F}})={\vec {OA}}\times {\vec {F}}=({\vec {OB}}+{\vec {BA}})\times {\vec {F}}={\vec {OB}}\times {\vec {F}}+{\vec {BA}}\times {\vec {F}}={\vec {OB}}\times {\vec {F}}$

deoarece BA și F sunt vectori coliniari.

• Punctul O se deplasează pe o dreaptă paralelă cu (Δ).
• Momentul unei forțe se schimbă dacă se schimbă polul din O în O₁:

${\vec {M}}_{01}={\vec {O_{1}A}}\times {\vec {F}}=({\vec {O_{1}O}}+{\vec {OA}})\times {\vec {F}}={\vec {M}}_{0}+{\vec {O_{1}O}}\times F.$

iar ${\vec {M}}_{o1}({\vec {F}})={\vec {M}}_{o}({\vec {F}})+{\vec {O_{1}O}}\times {\vec {F}}$ este legea de variație a momentului unei forțe la schimbarea punctului in raport cu care este calculat.

Momentul unei forțe în raport cu o axă

Momentul unei forțe în raport cu o axă

Componentele forței

Momentul unei forțe în raport cu o axă, de versor ${\vec {u}},$ este proiecția pe acea axă a momentului forței calculat în raport cu un punct oarecare al axei respective:

$M_{\Delta }={\vec {M}}_{0}\cdot {\vec {u}}=({\vec {r}}\times {\vec {F}})\cdot {\vec {u}}.$

Proprietăți

• $M_{\Delta }=0$ dacă cei trei vectori sunt coplanari: forța este paralelă cu axa Δ sau suportul forței intersectează axa.
• $M_{\Delta }=0$ nu depinde de alegerea punctului O pe axa Δ:

Astfel, dacă se consideră un alt punct O₁:

$M'_{\Delta }=({\vec {O_{1}A}}\times {\vec {F}})\cdot {\vec {u}}=[({\vec {O_{1}O}}+{\vec {r}})\times {\vec {F}}]\cdot {\vec {u}}=M_{\Delta }.$

• Momentul unei forțe în raport cu o axă Δ este egal cu mărime momentului produs de componenta forței dintr-un plan normal pe axă, calculat în raport cu punctul în care axa Δ intersectează planul normal:

$M_{\Delta }=({\vec {OA}}\times {\vec {F}})\cdot {\vec {u}}=[{\vec {OA}}\times ({\vec {F}}_{\perp }+{\vec {F}}_{\|})]\cdot u=({\vec {OA}}\times {\vec {F}}_{\perp })\cdot {\vec {u}}=\pm |{\vec {r}}\times {\vec {F}}_{\perp }|.$

Terminologie

• Momentul forței este tradițional notat de fizicienii români cu M_F, spre deosebire de fizicienii anglofoni, care îl notează cu litera greacă tau (τ).
• O formă tehnică a momentului forței e un cuplu de forțe constând din două forțe antagoniste acționând diametral la capetele aceluiași braț, dând momentul:

$M=F*r/2+F*r/2=F*r$

Vezi și

• Cuplu de forțe
• Momentul impulsului
• Teorema lui Varignon (mecanică)
• Dinamica elicopterului
• Rotor anticuplu

Bibliografie

• Mercheș, Ioan și Burlacu, Lucian: Mecanică analitică și a mediilor deformabile, Editura didactică și pedagogică, București, 1983.