Simbol Wythoff


În geometrie, simbolul Wythoff este o notație reprezentând o construcție Wythoff a unui poliedru uniform sau a unei pavări plane într-un triunghi Schwarz. A fost folosit pentru prima dată de Coxeter, Longuet-Higgins și Miller în enumerarea poliedrelor uniforme. Mai târziu, diagrama Coxeter a fost dezvoltată pentru a marca politopurile uniforme și fagurii din spațiul n-dimensional într-un simplex fundamental.
Un simbol Wythoff este format din trei numere și o bară verticală. Reprezintă un poliedru uniform sau o pavare uniformă, deși aceeași pavare/poliedru poate avea simboluri Wythoff diferite de la generatoare de simetrie diferite. De exemplu, cubul poate fi reprezentat prin 3 | 2 4 cu simetrie Oh sau prin 2 4 | 2 ca o prismă pătrată cu 2 culori și simetrie D4h, precum și prin 2 2 2 | cu 3 culori și simetrie D2h.
Cu o mică extensie, simbolul Wythoff poate fi aplicat tuturor poliedrelor uniforme. Totuși, metodele de construcție nu conduc la toate pavările uniforme din spațiul euclidian sau hiperbolic.
Descriere
[modificare | modificare sursă]Construcția Wythoff începe prin alegerea unui punct generator pe un triunghi fundamental. Dacă distanța acestui punct față de fiecare dintre laturi este diferită de zero, punctul trebuie ales să fie o distanță egală de fiecare margine. Apoi se trasează câte o perpendiculară de la punctul generator pe fiecare latură pe care el nu se află.
Cele trei numere din simbolul Wythoff, p, q și r, reprezintă colțurile triunghiului Schwarz utilizat în construcție, care au π⁄p, π⁄q și respectiv π⁄r radiani. Triunghiul este, de asemenea, reprezentat cu aceleași numere, scrise (p q r). Bara verticală din simbol specifică o poziție obligatorie a punctului generator în cadrul triunghiului fundamental în conformitate cu următoarele:
- p | q r : punctul generator se află în colțul p,
- p q | r : punctul generator se află pe latura dintre p și q,
- p q r | : punctul generator se află în interiorul triunghiului.
În această notație, oglinzile sunt etichetate prin ordinea de reflexie a vârfului opus. Valorile p, q, r sunt listate înainte de bară dacă oglinda corespunzătoare este activă.
O utilizare specială este simbolul | p q r care este destinat cazului în care toate oglinzile sunt active, dar imaginile reflectate impare sunt ignorate. Figura rezultată are doar simetrie de rotație.
Punctul generator poate fi pornit sau oprit față de fiecare oglindă, activat sau nu. Această situație creează 8 (2³) forme posibile, neglijând cea în care punctul generator se află pe toate oglinzile.
Simbolul Wythoff este similar funcțional cu mai generala diagramă Coxeter–Dynkin, în care fiecare nod reprezintă o oglindă și liniile dintre ele — marcate cu numere — unghiurile dintre oglinzi. (Liniile care reprezintă unghiuri drepte se omit.) Un nod este inelat dacă punctul generator nu este pe oglindă.
Exemple de pavări sferice, euclidiene și hiperbolice cu triunghiuri dreptunghice
[modificare | modificare sursă]Triunghiurile fundamentale sunt desenate ca reflexii în oglinzi și colorate alternativ. Succesiunea triunghiurilor (p 3 2) se schimbă de la sferică (p = 3, 4, 5) la euclidiană (p = 6), respectiv la hiperbolică (p ≥ 7). Pavările hiperbolice sunt prezentate ca o proiecții pe discul Poincaré.
| Simbol Wythoff | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 |
|---|---|---|---|---|---|---|---|---|
| Diagramă Coxeter | ||||||||
| Configurața vârfului | pq | q.2p.2p | p.q.p.q | p.2q.2q | qp | p.4.q.4 | 4.2p.2q | 3.3.p.3.q |
| Triunghiuri fundamentale | 7 forme și snub | |||||||
(4 3 2)
|
3 | 4 2 43 |
2 3 | 4 3.8.8 |
2 | 4 3 3.4.3.4 |
2 4 | 3 4.6.6 |
4 | 3 2 34 |
4 3 | 2 3.4.4.4 |
4 3 2 | 4.6.8 |
| 4 3 2 3.3.3.3.4 |
(5 3 2)
|
3 | 5 2 53 |
2 3 | 5 3.10.10 |
2 | 5 3 3.5.3.5 |
2 5 | 3 5.6.6 |
5 | 3 2 35 |
5 3 | 2 3.4.5.4 |
5 3 2 | 4.6.10 |
| 5 3 2 3.3.3.3.5 |
(6 3 2)
|
3 | 6 2 63 |
2 3 | 6 3.12.12 |
2 | 6 3 3.6.3.6 |
2 6 | 3 6.6.6 |
6 | 3 2 36 |
6 3 | 2 3.4.6.4 |
6 3 2 | 4.6.12 |
| 6 3 2 3.3.3.3.6 |
(7 3 2)
|
3 | 7 2 73 |
2 3 | 7 3.14.14 |
2 | 7 3 3.7.3.7 |
2 7 | 3 7.6.6 |
7 | 3 2 37 |
7 3 | 2 3.4.7.4 |
7 3 2 | 4.6.14 |
| 7 3 2 3.3.3.3.7 |
(8 3 2)
|
3 | 8 2 83 |
2 3 | 8 3.16.16 |
2 | 8 3 3.8.3.8 |
2 8 | 3 8.6.6 |
8 | 3 2 38 |
8 3 | 2 3.4.8.4 |
8 3 2 | 4.6.16 |
| 8 3 2 3.3.3.3.8 |
(∞ 3 2)
|
3 | ∞ 2 ∞3 |
2 3 | ∞ 3.∞.∞ |
2 | ∞ 3 3.∞.3.∞ |
2 ∞ | 3 ∞.6.6 |
∞ | 3 2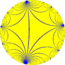 3∞ |
∞ 3 | 2 3.4.∞.4 |
∞ 3 2 | 4.6.∞ |
| ∞ 3 2 3.3.3.3.∞ |
Bibliografie
[modificare | modificare sursă]- en Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN: 0-486-61480-8 (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction)
- en Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN: 0-486-40919-8 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- en Coxeter, Longuet-Higgins, Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401–50.
- en Wenninger, Magnus (). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. pp. 9–10.
Legături externe
[modificare | modificare sursă]- en Eric W. Weisstein, Wythoff symbol la MathWorld.
- en The Wythoff symbol
- en Wythoff symbol[nefuncțională]
- en Greg Egan's applet to display uniform polyhedra using Wythoff's construction method
- en A Shadertoy renderization of Wythoff's construction method
- en KaleidoTile 3 Free educational software for Windows by Jeffrey Weeks that generated many of the images on the page.
- en Hatch, Don. „Hyperbolic Planar Tessellations”.
